


11 Hva er lys?
12 Refleksjon
13 Lysbrytning (refraksjon)
14 Optikk
15 Fargespredning (dispersjon)
16 Fargeblanding
17 Interferens
18 Lysmåling
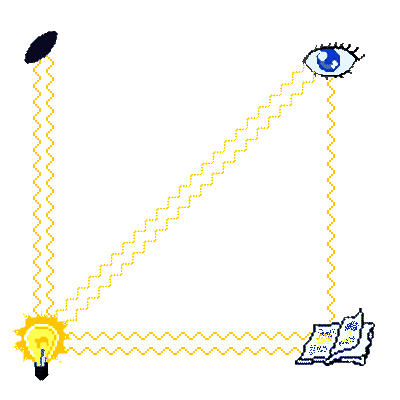
- Lys er energi som overføres fra lyskilde til det som mottar lyset. Lyset beveger seg svært fort (300 000 km/s). Når en lyskilde sender ut lys kalles det emisjon. Lys som treffer noe kan enten reflekteres eller sprees (=avbøyes i ulike retninger) eller så kan det bli absorbert og gå over til varme.
Eksempler:
Lys blir reflektert i et blankt speil
Lys blir spredt i en hvit flatet
Lys blir absorbert i en svart flate
Se animasjon: Hva er lys?

Barn vil relativt tidlig beherske begrepet lys på den måten at de kan peke og si hvor vi har eksempler på lys. Men om de med ord skal prøve å beskrive hva lys er, vil nok mange få problemer. Et svar på ovennevnte spørsmål er: Lys er energi. Energi kan videre defineres som det som får ting til å skje. I denne sammenhengen vil kanskje noen si at 'energi' er et vanskeligere begrep enn 'lys' og ovennevnte svar blir da en "forvanskning" i stedet for en forenkling. Her vil vi da understreke at lys er et grunnleggende begrep i den betydningen at det ikke finnes noen mer grunnleggende begrep som kan inngå i en definisjon. Forklaringer av slike grunnleggende begrep innebærer da at man bygger opp en forståelse ved å knytte ordet sammen med andre ord som har klare paralleller. Energi er da et slikt ord som forhåpentligvis skaper noen assosiasjoner som vi da også bør knyte opp mot begrepet lys. Lys vil alltid være "på farten" fra en lyskilde til en mottaker. Her vil vi da understreke at det er viktig å tenke på lys som en energiform som har med seg energi fra lyskilden til mottakeren. Betingelsen for at en lyskilde skal lyse er at det tilføres energi (elektrisitet til ei pære, kjemiske energi til et stearinlys osv). Den energien som er i lyset vil da overføres til mottakeren som da vanligvis blir litt oppvarmet. Når sollys treffer en vegg vil mye av lyset/energien absorberes og dermed blir veggen varm. Når lys treffer noe og slik omdannes til varme kaller vi det absorpsjon. Absorpsjon betyr at lys blir omdannet til andre energiformer, og varme er da den vanligste energiformen som lys blir omdannet til.
Når vanlig lampelys treffer en vegg er det snakk om relativt lite energi og vi vil vanligvis ikke observere at veggen blir varm. Det har da sammenheng med at det er snakk om svært små temperaturendringer. Likevel er det vanlig å si at lys alltid blir til varme når det skjer en absorpsjon.
Bildet til høyre viser i lyspære og et såkalt radiometer. Når det er lite lys som treffer vingene på radiometeret, så henger det i ro, men om vi belyser det med sterkere lys vil vingene gå rundt. Dette viser at lys er energi som f.eks. kan bli omdannet til bevegelser i radiometeret. Se aktivitetsdelen for en forklaring på mekanismen som gjør at vingene går rundt samt tips til hvordan man kan lage et radiometer selv.

Lys er bølge
Dette er et annet svar på spørsmålet om hva lys er. Folk flest vil nok oppleve 'bølge' som et vanskeligere begrep enn 'lys' og hensikten med dette svaret er da også å skape noen assosiasjoner som er nyttig når vi skal forstå ulike lysfenomen. Her vil vi kort nevne at en bølge har den egenskapen at den vil
beveger seg i alle retninger bort fra bølgekilden. Bølgen vil da etter som tiden går dekke et større og større areal samtidig som bølgehøyden blir mindre og mindre. Dette kan vi observere når vi kaster en stein på et stille vann. Det samme prinsippet gjelder da for lys. Nær lyskilden er lyset sterkt (svarer til stor bølgehøyde). Etterhvert som lyset sprer seg utover i rommet blir lysstyrken svakere og det har sammenheng med at lyset fordeler seg over et stadig større område. Videre er det slik at bølger har en tendens til å spre seg til alle steder hvor det er mulig å spre seg. Det innebærer blant annet at det vil være litt lys også i områder som vi kaller skygge. Den populære forestillingen om at lys går i rette linjer er altså ikke helt rett. I praksis vil litt lys bøyes inn i områder hvor det er skygge, men siden det er snakk om svært små mengder lys som bøyes inn i skygger, er det svært vanskelig å oppdage dette.
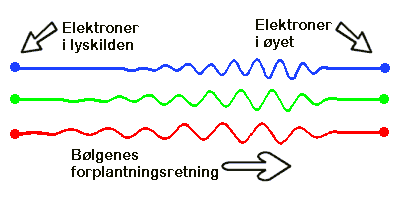

- Lys er bølger som forplanter seg utover fra lyskilden fordi elektroner vibrerer. Jo raskere elektronene vibrerer jo høyere er frekvensen. Bølgene som kommer fra lyskilden har ulike frekvenser. Øynene våre oppfatter ulike frekvensene som ulike farger fordi de påvirker ulike elektroner i øyet. Når elektronene i lyskilden vibrerer vil de sende ut bølger som så i sin tur får elektronene i øyet til å vibrere. Frekvensene som gir synlig lys er svært høye (ca 400 000 000 000 000 svingninger pr sekund i rødt lys).
Se animasjon: Sammenheng mellom farge og frekvens
Hva er grunnleggende forståelse
for begrepet lys?
Nå er det mulig å behandle lys og lyd uten å filosofere så mye på hva det egentlig er. Noen opplever dette som utilfredsstillende. Vanligvis er det de som har skjønt mest som også har lært å sette pris på grunnleggende forklaringer. De som har skjønt minst har kanskje aldri opplevd å forstå ulike naturfenomen og de etterlyser da heller ikke en grunnleggende forståelse. I prinsippet er det mulig å pugge et fagstoff slik at det kan gjengies til eksamen. Denne typen kunnskap vil imidlertid bli glemt relativt raskt og den er heller ikke særlig nyttig i praktiske situasjoner. Alternativet er å arbeide med et fagstoff både praktisk og teoretisk så lenge at man føler man har forstått hva det handler om og kan anvende den aktuelle kunnskapen i nye sammenhenger.
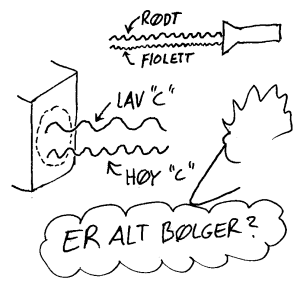

Bølger er grunnleggende
Her bruker vi begrepet bølge som er en fellesbetegnelse på lys og lyd og eventuelt andre bølger som det er aktuelt å undervise om i grunnskolen. En
grunn til å bruker endel tid på bølgebegrepet er at vi ønsker å rasjonalisere læreprosessen ved å konsentrerer oss om grunnleggende prinsipp som vi kan da anvende i flere sammenhenger. Det å se sammenhenger eller likheter i naturen er en viktig side ved det å forstå naturen. Bølger er en viktig side ved det meste som vi omgir oss med. De tre sansene syn, hørsel og varmefølsomhet vil alle motta bølger som så blir omdannet til nerveinpulser som registreres i hjernen. I tillegg til disse bølgene som vi kan oppfatte direkte har vi også gjort oss avhengige av ulikt utstyr som sender ut og mottar andre typer bølger. Eksempler er radio, TV, mobiltelefon, radar, sonar og annet. Også i disse tilfellene er bølgebegrepet grunnleggende for å forstå hvordan ting virker.
Å lære fysikk er som å bygge en grunnmur
Det å lære fysikk kan sammenliknes med å bygge en grunnmur. Hus bygges vanligvis på en grunnmur og hensikten med grunnmuren er da å gjøre huset stabilt og varig. Kunnskap om naturen er tilsvarende bygget på visse grunnleggende prinsipp. Grunnleggende kunnskaper har i denne sammenheng til hensikt å være et fundament som det er lett å bygge videre på. Hvis grunnlaget er varig og stabilt vil også påbygget være stabilt. Om grunnlaget er mangelfullt vil alle påbygninger også bli mangelfulle.
Lys er et viktig fenomen som mange synes er vanskelig å forstå. En årsak til dette har sannsynligvis sammenheng med at man i vanlige fysikkbøker har en tendens til å bruke to ulike byggeklosser i grunnmuren. I noen sammenhenger sier man at lys er små partikler (foton) og i andre sammenhenger sier man at man må betrakte lys som bølger. I praktiske tilfeller vil man bruke en type murstein i en grunnmur fordi dette gjør at steinene kan legges tett sammen i et overlappingsmønster som øker styrken i muren. Om vi derimot bruker stein med ulike størrelse og form, vil man sannsynligvis få problemer. Resultatet blir gjerne mange hull som gjør grunnmuren ustabil og ujevn slik at det er vanskelig å bygge videre på den.
I dette heftet vil vi da bare bruke en type stein i "grunnmuren". Det innebærer da at vi forklarer alle typer lysfenomen ved hjelp av en bølgemodell. I noen lærebøker kan man finne påstander om at dette er umulig, og av og til kan man henvise til den såkalte fotoelektriske effekten som da skal være et bevis på at noen lysfenomen ikke kan forklares om vi antar at lys er bølge. Her vil vi kort påstå at slike "partikkel-bevis" også kan forklares utfra en bølgemodell. Grunnen til at mange tror at partikkelmodellen er uungåelig, er sannsynligvis at de ikke har brydd seg med å sjekke bevisene. Her vil vi videre si at man i vitenskapelig sammenheng bør være skeptiske til "negative bevis" av typen "jeg har ikke sett/funnet/observert, derfor finnes ikke". De som sier at de representerer vitenskapen bør i det minste være så ydmyke at de innrømmer at andre kan ha sett lenger enn dem selv. Hovedpoenget i denne innledningen er imidlertid å oppfordre leseren til å konsentrere seg om en type byggeklosser når det gjelder å forstå lys og andre bølgefenomen. Hvis man prøver å blande inn partikkelmodellen når man skal forstå ulike lysfenomen, så viser erfaring at man får problematiske "hull" i forståelsen som skaper ulike problemer. Hvis man derimot bare konsentrer seg om bølgemodellen så vil man kunne bygge opp en tett og solid grunnmur som gjør at det er relativt lett å forklare alle typer lysfenomen. Her vil vi videre si det så sterkt at det ikke finnes noen seriøse forskere som mener at bølgemdellen for lys er feil. Hvorfor skal man da blande sammen to motsetningsfulle forklaringer av lys når man klarer seg med en forklaring som da gjelder for lys, lyd, vannbølger og mange andre naturfenomen. Det meste i naturen kan forklares på ulike måter, men et hovedmål i vitenskapelig sammenheng er da å finne fram til de beste forklaringene som forklarer flest sider ved de ulike naturfenomenen som vi observerer.

Lys går i tilnærmet rette linjer. Årsaken til at vi her bruker ordet 'tilnærmet' er at det finnes eksempler hvor vi kan observere at lys bøyes litt. Den populære forestillingen om at "lys går i rette linjer" som også står i L97, er derfor ikke helt korrekt. Men i småskolen er det vel ok å si at lys ikke går rundt hjørner og at det derfor blir skygger bak ugjennomsiktige gjenstander. Lys kommer alltid fra en lyskilder og tidlig i skoleverket er det aktuelt å undersøke lyset ved å observere skygger. Å lage skyggebilder er en vanlig aktivitet og i den forbindelsen er det nyttig å nevne noen generelle prinsipp for at elevene skal forstå hva som kjennetegner situasjoner hvor vi får skygger. Prinsipp 1: Skyggebilder forutsetter at det er en relativt sterk lyskilde. Lyskilden må altså lyse mye sterkere enn andre lyskilder. Dette forklarer da hvorfor ei lommelykt kan gi gode skyggebilder om kvelden når det er mørkt omkring, men dårligere skyggebilder om dagen. Prinsipp 2: Skyggebilder forutsetter også at lyskilden er relativt liten. Sola på en skyfri himmel og en enkeltstående lyspærer gir da skarpe og fine skygger. På en overskyet dag vil vi få omtrent like mye lys fra hele himmelen (en stor lyskilde) og tilsvarende vil lysstoffrør i taket ha en forholdsvis stor utstrekning og de derfor får vi svake eller diffuse skygger i slike tilfeller.

Ofte er det ubehagelig for øynene med for store kontraster (forskjell i lysstyrke) slik man f.eks. får ved sjøen i solskinn og innendørs om kvelden om vi bare har en liten sterk lyskilde. En måte å dempe kontrastene på er å la lyset gå gjennom en gjennomskinnelig flate som sprer lyset. En vanlig matt lyspærene har et slikt belegg på innsiden av glasset og det har da samme virkning som skyene på himmelen. Vi ser lyset fra sola når det er overskyet men ikke selve sola. Lyset fra sola treffer skyene og disse sprer det videre i alle retninger. Tilsvarende vil vi gjennom en vanlig matt pære se lyset fra glødetråden, men ikke selve glødetråden. Årsaken til dette er at skyene og pæreglasset er gjennomskinnelig men ikke gjennomsiktig. Det er aktuelt å lære barn forskjellen på gjennomskinnelig og gjennomsiktig. Gjennomsiktig betyr da at vi ser ting gjennom det over en viss avstand, mens et gjennomskinnelig stoff vil slippe lyset gjennom, men vi får da ikke noe klart bilde av det som er på andre siden fordi lyset sprees i alle retninger og gjør bildet diffust. Når et stoff ikke slipper lys gjennom kan vi kalle det ugjennomskinnelig eller lystett. Merk ellers at alle stoff blir gjennomskinnelige og gjennomsiktige når de bare blir tynne nok.
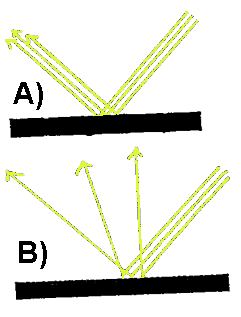
>Når får vi refleksjon?
Når vi underviser om lys, er det vanlig å starte med refleksjon. Alle barn har f.eks. sett et speil og de har da sannsynligvis også hørt om at speil reflekterer lys. Her vil vi da først se litt nærmere på hva som kjennetegner de situasjonene hvor vi får refleksjon. Når lys treffer plane (blanke, polerte, finslipte flater) vil lys reflekteres. Det er kanskje ikke alle som er klar over at hovedbetingelsen for at vi skal få det vi kaller refleksjon er at man har en plan flate. I et vanlig speil er det en tynn plan metallfilm (vanligvis aluminium) som reflekterer lyset. Metallfilmen befinner seg da på baksiden av glass som da beskytter den slik at den ikke reagerer med oksygen og blir matt. Men det er da også mulig å polere andre stoff som plast, stein og liknende og få en slags speilflate som da vil reflektere lys. En blankpolert bil vil f.eks. kunne gi et forholdsvis klart speilbilde, men i dette tilfelle vil endel av lyset nå litt inn i lakken og spredes tilbake på en diffus måte. Grunnen til at man bruker metaller i speil er da at disse reflekterer mestedelen av lyset fra overflaten, mens andre stoff vil slippe endel lys litt inn i stoffet og endel av dette lyset vil da bli absorbert av stoffet. Resten blir spredt tilbake og gjør at overflaten får farge.

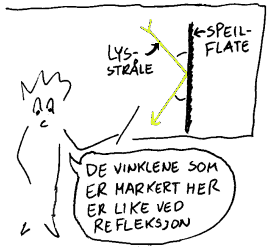
Hva er refleksjon?
Når vi beskriver refleksjon er det vanlig å tegne lyset som stråler som vist på figuren til høyre. En stråle som treffer en plan flate vil da bli reflektert tilbake i en bestemt retning. For å angi hva slags retning den reflekterte strålen får, har man formulert følgende lovmessighet:
Refleksjonsvinkelen er lik innfallsvinkelen.
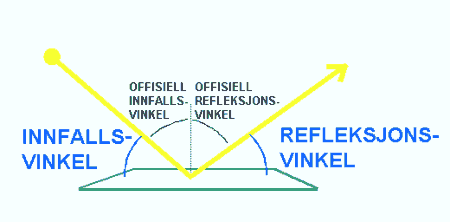
I prinsippet kunne innfallsvinkelen og refleksjonsvinkelen vært definert som vinkelen mellom speilflata og de respektive strålene, men man har da valgt å definere dem som vinkelen mellom strålene og innfallsloddet som i sin tur er definert som en tenkt linje som står normalt på speilflata i det punktet hvor strålen treffer speilflaten. I grunnskolesammenheng er det først og fremst viktig å gjøre elevene oppmerksom på at det er to vinkler som er like når en lysstråle blir reflektert. Siden innfallsloddet ikke er en fysisk gjenstand som finnes på et vanlig speil (den er en tenkt linje), så er vil vi her foreslå at man i grunnskolen henviser til vinkelene mellom speilflata og strålene siden elevene intuitivt vil tenke på disse når vi snakker om vinkler i forbindelse med speiling. Det betyr i tilfelle at de elevene som senere skal anvende f.eks. Snells brytningslov må gjennom en "omlæring" og lære den korrekte definisjonen av innfallsvinkel, refleksjonsvinkel og brytningsvinkel. I prinsippet er det mulig å definere en vinkel på ulike måter. Når det i dette tilfelle finnes en vinkel som er "korrekt", så er det fordi denne er blitt en slags internasjonal standard. Med de som har prøvd å undervise denne standarden kan ikke ha unngått å oppleve at elever svært ofte misforstår og tror at innfallsvinkelen er vinkelen mellom speilflata og innfallstrålen. Siden de færreste av elevene i grunnskolen vil få bruk for Snells brytningslov, mener vi her at det er bedre at de kan forklare lysfenomen på en enkel måte enn at de har hørt om en vanskelig standardmetode som de ikke klarer å huske eller anvende.
Bruk
av speil i skolen
Speil kan brukes i mange typer aktiviteter fra de som
er relativt enkle å forklare til svært kompliserte avbildninger.
De enkleste speilaktivitetene er knyttet til situasjoner hvor vi har en lysstråle
som treffer speilet og blir reflektert. I slike tilfeller er det relativt lett
å se at to vinkler må være like og i litteraturen er det vanlig
å si at refleksjonsvinkelen er lik innfallsvinkelen. Ovenfor
har vi begrunnet hvorfor vi anbefaler å henvise til andre enn de offisielle
vinklene i denne sammenhengen. Poenget her er at det er viktig å gi elevene
noen begrep som de kan bruke når de skal prøve å forstå
speiling. Videre bør de selv skal kunne forklare hva som skjer i ulike sammenhenger hvor
speil er involvert. Et mål er f.eks. at elevene klarer å tenke ut hvordan man må plassere et speil eller andre ting i forhold til et
speil for at man skal få en bestemt virkning. Det er alltid mulig å
komme til målet ved prøving-og-feiling-metoden, men om elevene
fortsetter å bruke denne metoden etter at de har lært om speil,
så kan vi vel sette et spørsmålstegn med om de har lært å bruke
speil.
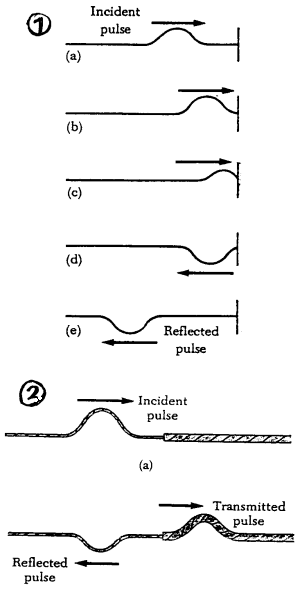
Vanligvis vil vi observere refleksjon når en lysstråle i luft møter et stoff som vi her vil kalle optisk tettere. Optisk tetthet er da en størrelse som forteller noe om hvor fort lyset beveger seg i de ulike stoffene. I et optisk tett stoff (eks metall, diamant, krystall ..) vil lyset gå relativt seint. I luft som da er et stoff med liten optisk tetthet vil lyset gå relativt fort. Siden vi befinner oss i luft vil de lysstrålene som omgir oss vanligvis møte stoff med større optisk tetthet når de treffer noe annet, og det er da i slike tilfeller vi får refleksjon. Men det vil også skje en refleksjon om en lysstråle treffer en flate med et optisk mindre tett område. Om vi f.eks. befinner oss under vann vil vi kunne observere at overflaten reflekterer lys som sendes opp mot overflaten. Mange vil oppfatte dette som "rart" og det er da naturlig å spørre hvorfor det er slik. En fullstendig forklaring av hvorfor det er slik, krever endel bakgrunnskunnskap som vi ikke forutsetter her. Et alternativ er da å vise til en analogi som illustrerer prinsippet. Det rare er altså at vi får refleksjon både når det er "mer optisk tetthet" og "mindre optisk tetthet" i det stoffet som lysbølgen treffer.
Analogien vi bruker her er da bølger på et tau. Vi antar først at vi tilfører energi til et tau ved å lage bølger på tauet. I den andre enden er tauet opphengt i et fast punkt (skrue i veggen). Se figur 1. En bølgetopp som møter det faste punktet vil ikke klare å bevege det faste punktet oppover og følgelig vil det faste punktet trekke bølgetoppen nedover i stedet. Det betyr at vi får reflektert en bølgedal slik figuren viser. (PSEp439) Veggen er med andre ord så tung at bølgen ikke klarer å rikke den og på den måten få overlevert energien. Derfor ble energien i bølgen reflektert tilbake. Om lys i luft treffer et optisk tettere stoff vil det få problemer med å bevege de elektromagnetiske feltene i dette stoffet. Jo større problemer, jo mer lys vil bli reflektert med motsatt fase (bølgedal i stedet for bølgetopp og omvendt). I naturen er det vanligvis snakk om mer eller mindre optisk tetthet, og figur 2 illustrerer da det som skjer når en lysstråle i luft treffer en vannflate. Det tykke tauet (vann) vil få overført litt energi fra det tynne tauet (luft), men noe energi blir da reflektert og forklaringen svarer da til den vi gav i tilfelle 1.

Hvis vi derimot tenker at tauet er festet til en mekanisme som lett kan gli oppover og nedover i takt med tauets bølgebevegelser (en ring på et rør) vil vi få et annet resultat. Også i dette tilfellet vil bølgetoppen ha med seg energi (figur 3), men i dette tilfellet klarer den heller ikke å få avlevert energien siden festet glir uten friksjon. Resultatet blir da en motsatt rettet bølge som tar energien med tilbake. Vi får altså en reflektert bølge uten faseforskyvning fra en tauende som ender i "ingenting" (PSEp440). I naturen vil vi aldri finne steder med "ingenting". Selv i vakuum er det noe (eter) som kan motta energien i lys. Figur 4 illustrerer da det som skjer når en lysbølge i vann møter luft eller vakuum. Lys som kommer fra et optisk tettere medium (vann) og møter et optisk mindre tett medium (luft), vil føle at det er vanskelig å finne steder å avlevere all energien og det vil da skje en delvis refleksjon. De elektromagnetiske svingningene som oppstår på grensen mellom vann og luft vil da føre til at en stor del av lyset blir reflektert tilbake inn i vannet. I visse tilfeller vil man også få totalrefleksjon. Totalrefleksjon betyr da at all energien sendes tilbake til mediet med størst optisk tetthet. Mer om totalrefleksjon i forbindelse med oppgavene.
En lysbølge vil først "oppdager" at det mangler noe som kan ta opp energien etter at den er kommet litt ut i det optisk lettere stoffet. Finmålinger i forbindelse med optisk fiberteknologi viser at det synes som om bølgen reflekteres fra en flate som tilsynelatende ligger en tanke utenfor det egentlige skillet mellom de to stoffene. Dette kalles Groos-Hächer effekt.
Når vi forklarer speiling glemmer vi vanligvis å si noe om at det vanligvis skjer et bortfall eller en tilførsel av ekstra lys i en plan flate. Dette kan virke forvirrende når man i speilflater observerer at vi ser noe annet enn den litt firkantede speilforklaringen ovenfor forteller. Det er viktig at vi gjør elevene oppmerksom på dette, ellers er det store sjanser for at de glemmer det vi har lært dem om speiling fordi det ikke fungerer i praksis. Et eksempel. Ei vanlig glassrute fungere som et speil i visse situasjoner og ikke i andre. Hva er årsaken? Prinsippet er at det speilbildet vi ser under bestemte betingelser er reflektert lys fra glassruta. Men i tillegg til dette lyset, så kan det også komme annet lys fra glassruta som ikke er reflektert. Om dette er sterkere enn det reflekterte lyset, vil vi ikke se speilbildet selv om det er der. Når det er mørkt ute kan vi på innsiden se et speilbilde av oss selv og tilsvarende kan vi fra utsiden se et speilbilde av sol og fjell i et vindu. Hvis det derimot er lysere på den andre siden av vinduet, så vil dette lyset overdøve det speilbildet som "vår side" lager.

Generelt bør vi altså kommentere styrkeforholdet mellom det lyset som går gjennom glasset og det lyset som blir reflektert i glasset. Dette betyr f.eks. at ei plan flate kan forårsake at to bilder blandes sammen om lyset fra dem er noenlunde like sterkt. Hvis vi f.eks. tenker på ei speilblank vannflate så vil vi i denne se både himmelen over oss og bunnen under vannflata. Tilsvarende vil da også fiskene under vannet kunne se både ting over vannflata og ting under vannflata når den ser opp mot overflata.
I forbindelse med speiling er det to tilnærmingsmetoder som har tilknytning til hva vi fokuserer på. Den enkleste og vanligste metoden man bruker i grunnskolen er å fokusere på lysstråler. Den andre metoden er å fokusere på avbildning. I det første tilfellet følger man på en måte lysstrålene fra det som sender ut lyste til det som mottar lyset. I det andre tilfellet tar vi utgangspunktet i observatøren (mottakeren av lys) og følger på en måte strålene bakover og konsentrerer oss om virtuelle bilder som vi ser. Det vi ser bak speilet på badet er altså ikke der det synes å være, men vi sier at det er en avbildning. Denne vekslingen mellom to tilnærmingsmetoder kan virke forvirrende og her vil vi prøve å holde dem mest mulig adskilt fra hverandre.
Et annet problem er begrepsbruken vår i forhold til hva vi ser. Er f.eks. en lysstråle synlig eller usynlig? En laser sender f.eks. ut en relativ smal lysstråle og om luften er klar vil vi ikke se noe der strålen ikke treffer annet enn luft. Men om vi lager litt røk, vanndamp eller lar den gå gjennom vann med litt melk oppi vil vi tydelig se det vi vanligvis kaller en stråle. I denne sammenhengen er det viktig å fortelle for elevene at vanlig lys er sammensatt av mange lysstråler og lysstråle er ikke bare det vi kan se når en smal lysstråle går gjennom et lite hull eller liknende.
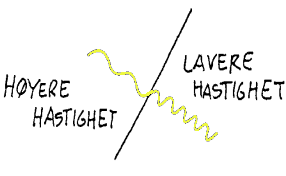
Lys kan endre retning når lysfarten endres
I skoleforsøk er det ikke mulig å måle lyshastigheten direkte ved hjelp av f.eks. stoppeklokke. Lyshastigheten er rett og slett for stor. Lys har en fart på 300 000 km/s i vakuum og nesten like høy hastighet i luft. Vi kaller lyshastigheten i vakuum for c (c=300000km/s). Lyshastigheten i atmosfæren (luften) som omgir oss er ca 99,97% av c som da er tilnærmet lik c. Selv om lysfarten i vakuum og lysfarten i luft er nesten like er det likevel mulig å se at lys går ulikt fort i luft med ulik temperatur på tross av at det er snakk om svært små endringer i lyshastigheten (hundredeler av 1%). Kald luft har større tetthet enn varm luft og når lys går gjennom områder med store temperaturforskjeller vil vi kunne se at lysstrålene bøyes. Årsaken til bøying av lysstråler er at lyset har ulik hastighet på steder med ulik optisk tetthet. I skolen kan vi ikke måle at lysfarten endrer seg, men vi kan da observere og måle hvor mye en lysstråle bøyes, og derfor kan vi indirekte observere og beregne hva lyshastigheten er i ulike medier. Her følger først en oversikt over brytningsindeksen i noen ulike optiske medier:
Stoff |
brytningindeks n=c/v |
lysfart i % av c |
vakuum |
1 |
100% |
luft |
1,0003 |
100% |
vann |
1,33 |
75% |
glass |
1,5 |
67% |
krystall |
1,7 |
59% |
diamant |
2,4 |
42% |
Brytningsindeksen for et medium er definert som forholdet mellom lyshastigheten i vakuum og den aktuelle lyshastigheten. Dette er da et tall som blir større jo seinere lyset går. For å få en oversikt over forholdet mellom de ulike hastighetene, så har vi i tabellen ovenfor føyd til et prosent-tall som gir en klarere forståelse for hvor fort lyset egentlig går i de ulike mediene.
Hvordan kan vi forklare årsaken til at lys bøyes?
Lys er bølger. Til høyre har vi tegnet slike bølger som beveger seg fra luft på skrå inn mot glass. Når en bølgetopp passerer overgangen mellom luft og glass vil den gå seinere og avstanden mellom to bølgetopper vil da bli ca 67% kortere fordi de vil gå ca 67% seinere. Frekvensen eller antall bølger pr sekund vil derimot være det samme over alt og det vil derfor ikke bli noen opphoping av bølger. Alle bølgetoppene vil ha en tid hvor de er delvis utenfor og delvis innenfor glasset, men de vil hele tiden henge sammen. Dette betyr da at bølgetoppene vil bøyes slik figuren viser. Hvis vi så tegner lyset som stråler (piler) i stedet for bølgtopper vil vi få en tilsvarende bøying i disse strålene. Lysets bevegelse er alltid 90° i forhold til bølgetoppene og vi får da piler som viser hvordan lyset beveger seg når det går på skrå mellom luft og glass. Her har vi da prøvd å forklare hvorfor lys bøyes ved å tegne bølgetopper i to medier med ulik bølgefart. Hvis vi tenker oss at lyset går motsatt veg fra glass til luft får vi den samme figuren med de samme vinklene. Det betyr at brytningen av en lysstråle blir like stor enten lyset går fra luft til glass eller omvendt.

En annen måte å forklare hvorfor en lysstråle bøyes når den går på skrå mellom medier med ulik optisk tetthet er å tenke at lys har en utstrekning på tvers av fartsretningen. Vi kan altså tenke at lys har "skuldrer" som stikker ut på hver side av lysstrålen. Når så lyset passerer på skrå mellom luft og glass vil det et kort øyeblikk oppleve at de to skuldrene er i medier som har ulik hastighet. Det betyr videre at lyset får en bøying som skyldes at den "skuldra" som er i luft vil bevege seg litt fortere enn den "skuldra" som er i glasset. Denne populariserte forklaringen kan da være utgangspunkt for en enkel regel som da gjelder for all lysbøying i alle tenkte situasjoner. Vi tenker oss da at lyset befinner seg i overgangen mellom to medier med ulik lyshastighet. Regelen er da:
Lys som går mellom medier med ulik optisk tetthet vil bli avbøyet mot mediet med lavest lysfart (størst brytningsindeks).
Hvis lysstrålen er 90° i forhold til grenseflaten vil det ikke skje noen avbøyning fordi den optiske tettheten er like stor på begge sidene av lysstrålen (men ikke foran og bak). I dette tilfellet vil det bare foregå en endring av lyshastigheten, men altså ikke noen avbøyning. Om fartsretningen derimot er på skrå i forhold til grenseflata mellom de to områdene med ulik lyshastighet vil lyset i overgangsøyeblikket ha ulike medier til høgre og venstre og da forteller regelen at bøyingen alltid vil skje mot den siden hvor "skulderen går seinest". Denne regelen sier da ikke noe om hvor stor avbøyningen blir, men den sier da bare hvilke retning avbøyningen blir. Regelen er videre en "logisk" følge av en antakelse av at lyset har utstrekning på tvers av fartsretningen og derfor bør den være relativt lett å huske. Den gjelder da både når lyset går fra luft til glass og omvendt. Vi kan da tenke at bøyingen skyldes at den ene "skulderen" møter mer "motstand" enn den andre ide lysstrålen går på skrå mellom områder med ulike lyshastighet.
Luftspeiling er et fellesnavn på situasjoner hvor lys blir avbøyet fordi det går gjennom områder med ulik lufttemperatur og dermed ulik optisk tetthet eller lysfart. I lærebøker og annen litteratur kan man finne vanskelig og ofte feilaktige forklaringer på årsaken til ulike luftspeilingsfenomen. Årsaken er kanskje at det er vanskelig å bruke den tradisjonelle Snells brytingslov for å forklare disse fenomenene. Her vil vi derimot viser hvor enkelt slike fenomen kan forklares ved hjelp av lovmessigheten som er brukt her. I ørkener kan man få store temperatursvingninger og derfor hører man også ofte om luftspeilinger i slike områder. Her vil vi derimot forklare de to vanligste luftspeilingene man kan observere i Norge.
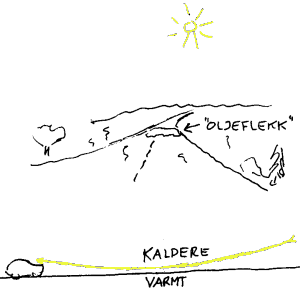
Den første er "oljeflekker på asfalt" som kan sees på varme dager når sola skinner. På relativt rette veier kan det da av og til se ut som om det er større flekker med vann eller olje lenger framme på veien. Når vi så kommer nærmere forsvinner de. Fenomenet skyldes at asfalten og luften rett over er svært varm mellom oss og den tilsynelatende flekken. Det betyr da at denne luften har mindre optiske tetthet og dermed større lyshastighet enn den omliggende litt kjøligere luft. Det som da i virkeligheten skjer er at lys fra himmelen foran oss vil komme på skrå inn i overgangen mellom den varme luften nederst og den litt kaldere luften litt lenger oppe. Regelen ovenfor sier da at lysstrålene da vil bøyes mot det området som har størst optisk tetthet, det vil si den kjølige luften lenger oppe. Resultatet blir da at lyset vil bøyes oppover slik figuren viser. For oss vil det da se ut som om lysstrålene som egentlig kom fra himmelen, kommer fra veien. En naturlig tolkning er da at lys fra himmelen er blitt reflektert i en eller annen væske (vann eller olje) på vegen. Den rette forklaringen er da at lyset er blitt bøyet i luftlagene over asfalten.

Den andre vanlige luftspeilingen vi kan observere i Norge er "svevende øyer". Dette kan man oppleve langs hele kysten, oftest i tidlige morgentimer (hildringstimen) før solgangsbrisen gjør seg gjeldene. Hvis man da står lavt nede ved stranden og ser utover mot fjerne øyer og holmer kan det se ut som om disse svever. Vi ser med andre ord himmel mellom toppen av øya og havflata. Dette fenomenet har da sammen forklaring som i eksemplet ovenfor. Fenomenet inntreffer når lufttemperaturen er lavere en sjøtemperaturen og vi vil da få en situasjon hvor luften nærmest havoverflata er varmere enn luften lenger oppe. Lysstråler som da kommer fra over de fjerne øyene på skrå innover mot oss kan da bli så mye bøyet oppover i overgangen mellom varm luft nær sjøen og kaldere luft litt lenger oppe at det ser ut som om disse strålene kommer fra nedre kant av øyene. I praksis vil vi da se toppen av øyene der disse virkelig er, men lenger nede ser vi da himmelen, og det er da denne "omsnuingen" som gjør at det ser ut som om øyene svever.
Funklende stjerner Ved klare kalde netter ser man ofte at stjernene blinker. Sterke stjerner som står lavt over horisonten blinker mest og disse kan da også blinke i forskjellige farger. Forklaringen er da at lyset som når oss går gjennom urolige atmosfæriske områder hvor de ulike delene av lyset blir mer eller mindre forsinket. Resultatet blir da tidvis opphoping og uttynninger av lysstrålene. (Denne variasjonen av lyshastigheten i atmosfæren gjør at det er grenser for hvor små detaljer vi kan se i kikkerter som er plassert ved jordoverflaten. Jo mer vi forstørrer jo mer vil temperaturforandringene i luften forstyrre bildene våre.)
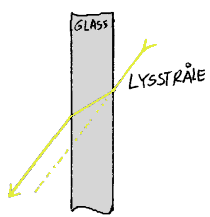
Paralellforskyvning
Luft/glass Lys som går gjennom glass har lavere hastighet enn lys som går gjennom luft. Noen vil da kanskje tenke at et vindu vil bøye lysstrålene slik at det vil se ut som om det som er på baksiden har forflyttet seg. Tilsynelatende er ikke dette tilfelle og her vil vi kort kommentere hva som skjer når lys går på skrå gjennom en vindusrute. Figuren viser at lys vil bøyes når det går gjennom et glass med to parallelle sider. Den lysstrålen som kommer ut vil da være parallell med den innkomne lysstrålen fordi bøyingen i de to tilfellene er like stor men motsatt rettet. Den utgående lysstrålen vil derimot være litt forskjøvet til siden etter at den har gått gjennom glasset, men denne forskyvingen er da så liten at vi vanligvis ikke oppdager den.
Optikk handler om å utnytte lysets egenskaper i ulike instrument. I denne sammenhengen er glass et nyttig og rimelig materiale. Om vi har tilgang på løse linser, er det mulig å la elevene selv lage ulike optiske instrument. Sentrale begrep som objekt, okular, brennvidde, brennpunkt, bilde, speiling ol. vil da kunne bli nyttige hjelpemidler, i stedet for puggeobjekt.
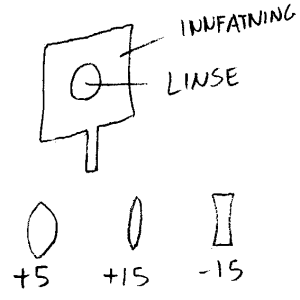
Problemer med å skaffe utstyr til fysikksløyd
Siden glass er et rimelig og enkelt materiale å arbeide med, er fysikksløyd aktuelt når det gjelder optikk. Den tekniske utviklingen har imidlertid ført med seg at det er relativt vanskelig å få kjøpt f.eks. enkle billige
linser. Det er i dag lite marked for slike billige linse uten høy presisjon.
De linsene som optikerne brukte før var nøyaktig slipt og derfor
dyre. I dag er det imidlertid vanlig å bruke kontaktlinser i stedet for
briller og det kan derfor være vanskelig å få tak i enkle
linser. Det
er derimot mulig å få kjøpt linser til skolebruk, men disse
er da vanligvis ferdigmontert i spesielle rammer og om man ønsker å
lage optiske instrument selv må man vanligvis plukke linsene ut av rammene
som kanskje utgjør storparten av den relativt høye prisen. Om
det er vanskelig å skaffe enkle linser er det desto letter å skaffe
monteringsutstyr for hjemmelaget optikk. Tørkeruller og doruller har en kjerne som vanligvis kastes. Disse har en diameter omkring 5 cm
og siden diameteren ikke er standardisert vil vi ofte finne at slike ruller
passer inn i hverandre. Mange linser som er beregnet til skolebruk, har også en diameter omkring 5 cm. Disse kan da plasseres inni rullene.
Dette gjør at man relativt enkelt kan lage f.eks. kikkert og mikroskop.
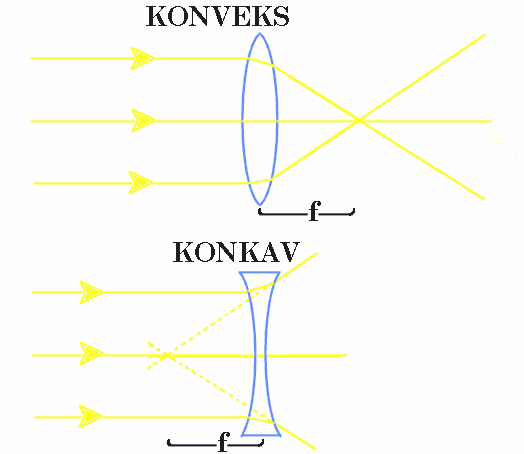
To typer linser
I skolesammenheng oppgis vanligvis brennvidden(f) for å angi styrken på en linse. Eksempel på praktiske brennvidder til skolebruk er f = +5, +10, +15 +30 og -15. Fortegnene angir om linsene er konveks (samlelinser=+) eller konkav (spredelinser= -). En
huskeregel er at konvekse linser vokser mot midten mens konkalve linser avtar
mot midten. I skolen er det vel like bra å bruke navnene samlelinse og
spredelinser siden disse navnene forteller litt om funksjonen til linsene. Hos optikere brukes fortegnene på samme måte, men i stedet for brennvidde eller fokusverdi
(f), bruker de en verdi som de kaller diopter (D). Sammenhengen mellom disse to er gitt av formlene: f=100/D eller D=100/f. Hos optiker regner vi kanskje ei linse med verdi 3 som en relativt sterk linse. Siden det tilsvarer en brennvidde på omkring 30 vil vi i skolesammenheng regne dette som en svak linse.

Hva kan ei samlelinse brukes til? Figuren ovenfor viser at når parallelt lys treffer ei samlelinse vil lyset samles på baksiden i et punkt som vi kaller brennpunkt. Avstanden fra linsa til brennpunktet kalles brennvidde (f). Lyset fra sola er tilnærmet parallelt og alt lyset som treffer ei samlelinse vil da samles i et punkt. Det betyr videre høy konsentrasjon av energi og vi kan få ting (plapir ol) til å brenne ved hjelp av et slikt brennglass om diameteren på linsa er stor nok. Jo større diamenter, jo mer sollys vil samles i brennpunktet.
Ei samlelinse kan også brukes som lupe. Figuren til høyre viser hvordan strålene fra ei rød pil går gjennom ei lupe før de treffer øyet vårt. For observatøren vil det da se ut som om lyset kommer fra ei større pil slik som den som er stiplet. Merk at objektet (pila som vi ser på ) må være nærmere linsa enn brennpunktet. Om vi holder ting lenger unna vil vi kunne oppleve at vi får et bilde av objektet som er opp-ned.


Ei samlelinse kan gi ei avbildning. Merk at det som er stiplet i lupe-eksempelet ovenfor ikke er reelle bilder eller stråler, men noe som vi kan kalle immaginære bilder/stråler. Men det er også mulig å lage reelle avbildninger ved hjelp av ei samlelinse og det er da vist i figuren til venstre. I dette tilfellet har vi ei pil som vi kaller objekt og på andre siden av linsen har vi et papirark eller liknende hvor vi kan få en avbildning av objektet. I prinsippet er det mulig å få en slik avbildning også ved hjelp av et lite hull der hvor linsen er plassert. De tykkeste gule linjene viser da hvordan lyset vil gå i dette tilfellet. Problement med denne avbildningen gjennom et lite hull, er at avbildningen blir lyssvak og det er da bare i spesielle tilfeller hvor det er mye lys fra objektet og lite lys på baksiden at vi vil se avbildninger gjennom et hull. Når vi derimot erstatter hullet med ei linse vil avbildningen få mer lys. Alle de tynne gule linjene på figuren representerer stråler fra tuppen på pila som vil samles i tuppen av avbildningen. Vi kan med andre ord si at alt lys fra objektet som treffer linsa vil samles i en forholdsvis lyssterk avbildning på baksiden. Dette prinsippet for avbildning har vi i fotoapparat og i øyet. Ved silke avbildninger er det nødvendig å stille skarpt. I et fotoapparat skjer det ved å endre på avstanden fra linsa til filmen. I øyet skjer det ved at musklene som holder linsen endrer på brennvidden (endrer krummingen på linsa) slik at avbildningen på netthinnen blir skarpt. Øyet vårt er videre skapt for å kunne se i svært mye og svært lite lys, og i den sammenhengen vil regnbuehinnen regulere hvor mye lys som slippes gjennom. Når det er sterkt sollys vil pupillen være et lite hull, men i mørket vil det slippe mye mer lys gjennom linsen. På netthinnen er det et mindre område med spesielt mange lysfølcomme punkt og dette området kalles den gule flekk. Det er hver vi ser en skarp avbildning. Det betyr med andre ord at storparten av det øyet ser er diffust eller uskarpt, men det relativt lille området vi ser på vil da være uskarpt. Når vi ikke til daglig registrerer det som er uskarpt er det fordi øyet automatisk vil sørge for at avbildningen av objektet vil falle på den gule flekken. Merk ellers at bildet på netthinnen og i fotoapparatet er opp-ned.
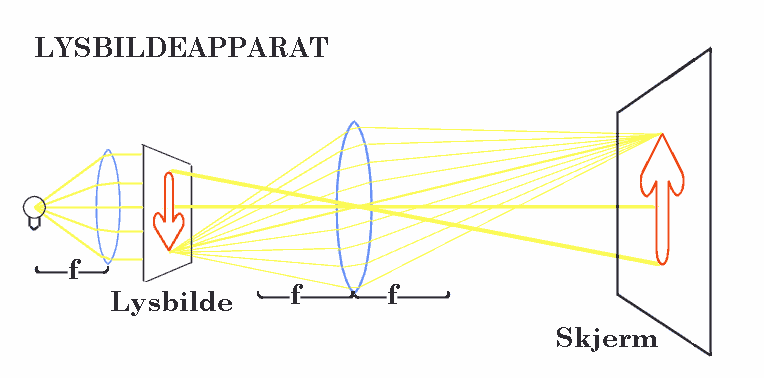
I skolesammenheng er det aktuelt å bruke ulikt optisk utstyr og det er da aktuelt å forklare virkemåten til det. Det faktisk også ganske enkelt å lage modeller av endel utstyr om man har tilgang på noen samlelinser. Det som følger her er derfor ment å være et teoretisk utgangspunkt for at elevene selv kan prøve å lage lysbildeapparat, kikkert og mikroskop. Den prinsipielle virkemåten til et lysbildeapparat er vist til venstre. Denne viser da at hovedprinsippet er en avbildning hvor objektet er lysbildet som står på hodet, og på en skjerm får man da en avbildning. Hensikten med linsen på den andre siden av lysbildet er da bare å samle mest mulig lys som treffer lysbildet. Jo mer lys som treffer lysbildet, jo mer lyysterkt vil avbildningen på veggen bli. Når vi plasserer ei lyspære e brennpunktet for ei linse vil lyset på baksiden bli parallelle stråler som er nyttige i mange sammenhenger.
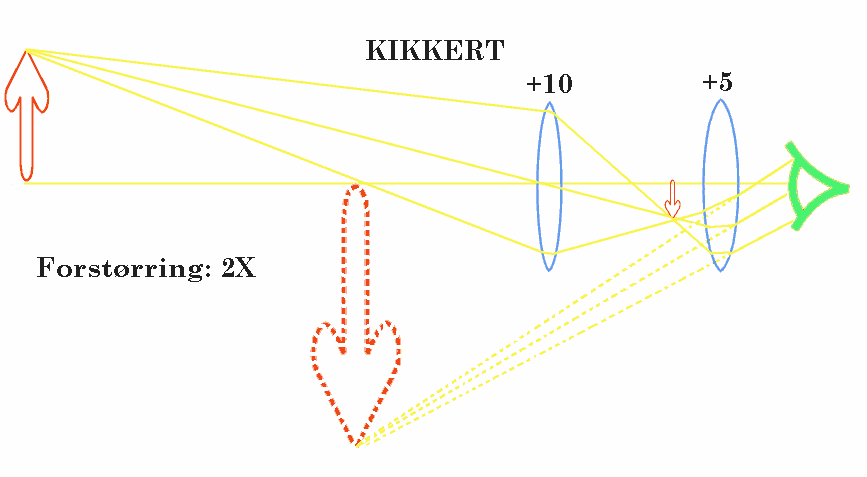
Virkemåten til en kikkert er mer komplisert en de forholdsvis enkle avbildningene som vi har vist ovenfor. Hovedgrunnen er vel at vi i en kikkert har både en avbildning og en forstørring med et imaginært bilde, og det er da ikke alltid så enkelt å forklare hva som virkelig skjer. Lærebøker unngår ofte å forklare kikkerten. Her vil vi da påstå at det kanskje ikke er så vanskelig å forstå kikkerten som mange tror. Figuren til høyre viser da at objektet (pila til venstre) vil få en vanlig avbildning gjennom objektivet (linsa til venstre) og dette bildet er da tegnet som en liten pil mellom linsene. Hadde vi f.eks. plassert et papirark her ville vi sett avbildningen. Men i stedet for å gjøre det, velger vi heller å "se på denne avbildningen med ei lupe". Som nevnt ovenfor gir ei lupe et imaginært eller et tilsynelatende bilde. Om vi så forlenger de tre gule strålene som er tegnet på figuren, vil vi se at disse vil samles i et stort stiplet imaginært bilde, og det er da dette vi ser i kikkerten. I dette tilfellet hvor objektivet har en brennvidde som der det dobbelte av okularet (linsa nærmest øyet) får vi en forstørring på 2 (dobbling av synsbildet). Det er med andre ord forholdet mellom de tro brennviddene som bestemmer forstørrelsen til kikkerten. Merk ellers at kikkerten som er vist ovenfor gir en avbildning som er opp-ned. Dette er upraktisk og de fleste kikkertene som selges i dag er såkalte prismekikkerter hvor det mellom linesene er plassert noen prismer (speil) som gør at bildet snues opp-ned og vi ser da et rettvendt bilde. Den enkleste måten å lage en kikkert på er å holde to linser foran øyet og man vil da kunne se hvor mye forstørringen er ved å sammenlikne det vi ser gjennom linsene i det ene øyet og det vi ser utenom linsene med det andre øyet.
Mange har sett at vi får en mikroskopvirkning om vi kikker feil vei i en kikkert. Her vil vi da kort nevne at om vi bytter plass til linnsene i figuren ovenfor (den svakeste linsen nærmest øyet) så vil vi få et mikroskop. Også i dette tilfellet er det lett å lage et mikroskop ved å holde to linser foran det ene øyet. Om vi så også ser på objektet med det andre øyet utenfor linsene er det relativt lett å se hvor mange ganger mikroskopet forstørrer.
Hvitt lys består av ulike farger med ulik styrke
Se animasjon: Hvitt lys kan spaltes i farger


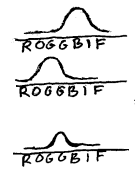
-Menneskets øye kan se bølger med frekvenser mellom ca 400THz og 750THz. Det er vanlig å si at lys består av 7 farger selv om spekteret viser at det er snakk om mange ulike fargenyanser. Huskeregel: ROGGBIF
Så langt har vi sagt at lys har ulik fart i ulike medier og dette forårsaker da at lysstråler bøyes. Det er grunnleggende at elevene forstår dette og i de tilfellene hvor vi arbeider med hvitt lys eller ensfarget lys (fra laser el.) er dette grunnregelen som vi bør bruke når vi skal forklare ulike lysfenomen. Men denne grunnregelen er ikke tilstrekkelig om vi skal forklare fargefenomen. Egentlig er det feil å behandle lys som en størrelse som har en fart i et bestemt medium. Tidligere har vi nevnt at lyshastigheten i glass er 67% av c men dette er da bare tilnærmet rett. I virkeligheten er det da slik at rød lys har en hastighet omkring 67% mens fiolett lys har en hastighet omkring 66%. Hvitt lys består med andre ord av ulike farger som da har ulik fart i ulike medier og i glass vil da fartsforskjellen være i størrelsorden 1% når vi regner prosent i forhold til lyshastigheten i luft/vakuum.
Hvitt lys består av lys med ulike farger eller frekvenser.
Figurene ovenfor gir da en litt grov sammenheng mellom frekvens og farge. Generelt er det øyet vårt som definerer hva vi mener med lys.I praksis har det vist seg at ulike mennesker ser farger litt ulikt og de frekvensgrensene vi opererer med mellom ulike farger er derfor usikkre. Lys er det vi kan se med øynene og forsøk har da vist at mennesker normalt kan se elektromagnetiske bølger med frekvens mellom ca 400THz (T='tera'=1012) og 750THz. Hvitt lys er da vanligvis en blanding av alle frekvenser mellom disse ytterpunktene.
Hvitt lys kan deles i ulike farger fordi lysfarten til fargene varierer
Hastigheten til de ulike fargene/frekvensene er tilnærmet den samme i vakuum og luft, men nøyaktige målinger viser at fiolett lys går litt seinere enn rødt lys i luft. Når det derimot gjelder glass og andre stoff er det større forskjell i farten til fiolett og rødt lys. Nedenfor har vi antydet hvor stor fart de ulike fargene har i glass sett i forhold til c. Hensikten med tallene er at man skal få en følelse av hvor store fartsforskjeller det dreier seg om for ulike farger i glass.
Lysfart i glass som prosent av c:
Rødt Orange Gult Grønt Blått Indigo Fiolett
66,7% 66,6% 66,5% 66,4% 66,3% 66,2% 66,1%

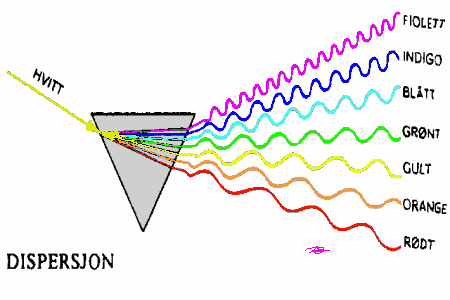
Tidligere har vi nevnt at lysbrytingen når lys går på skrå mellom luft og glass, er bestemt av lyshastigheten i glasset. Når hastigheten er litt forskjellig for de ulike fargene betyr det at de vil brytes litt forskjellig når de går inn i (og ut av) glasset. Fiolett lys vil da brytes mest og rødt lys minst. Når så lys går på skrå gjennom et vindusglass eller et firkantet prisme vil fiolett lys brytes mest hver gang. Det betyr da at fiolett og rødt lys har litt forskjellig retning mens de er inni glasset, men når lysstrålene så går ut igjen av glasset vil de få samme retning som de hadde før de traff glasset. Årsaken er at brytningen i de to flatene har motsatt retning og totalbrytningen blir da lik for både rødt og fiolett lys (0°).
Hvis vi derimot sender en lysstråle inn i et trekantprisme vil vi oppleve at brytningen når lyset går inn i prismet og brytningen når lyset går ut av prismet blir i samme retning. Se figur. I dette tilfelle vil vi da kunne se at de forskjellige fargene skiller lag og vi vil da se at fiolett lys brytes/bøyes mest mens rødt lys brytes minst. Vi får med andre ord et spektrum. Et spektrum er da det man får når man sprer de ulike fargene i lys ut langs en linje.
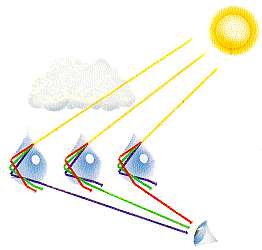
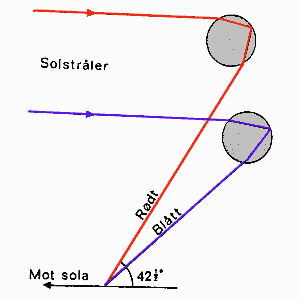
Regnbuen oppstår når sollys treffer vanndråper/regndråper som svever i luften. Det vil da skje en bøying av lysstrålene når de går inn og ut av vanndråpen, og dette vil vi da kunne se som en regnbue på himmelen. Figuren til venstre viser den vanligste strålegangen vi får i en regnbue. Figuren viser tråler for rødt og fiolett lys og de andre fargene vil da brytes mellom disse yttergrensene. Regnbuen vil danne en ring som har en vinkel på ca 42° i forhold til en linje gjennom sola og observatøren.
Foran har vi vist hvordan hvitt lys kan deles eller spredes opp i et spekter som består av ulike farger. Når det er mulig å dele opp lys og få nye farger er det også mulig å samle eller blande lys tilbake til de opprinnelige fargene. Her vil vi da gi noen praktiske eksempler på fargeblanding. Generelt er det mulig å blande farger på to prinsipielt ulike måter og disse kalles da additiv og subtraktiv fargeblanding.


Additiv fargeblanding
Hvis man i utgangspunktet har lysstråler som har ulike farger og så blander dem vil de ikke utestenge hverandre men summeres sammen og derfra kommer ordet additiv. Eksempler på slik fargeblanding er det vi får når lyskastere med ulike farget lys møtes, og det som da skjer på en TV og dataskjerm. I det siste tilfellet finnes det svært små punkter på skjermen som enten er røde, grønne eller blå/indigo (RGB) og om alle disse små prikkene lyser maksimalt vil vi oppfatte lyset fra dem som hvitt. Figuren til høyre viser dette prinsippet. Det der da mørkt omkring for å understreke at det i disse tilfellet er selve lysstrålene som blandes. I praksis viser det seg at vi ikke behøver å alle de 7 ovennevnte fargene for å få hvitt lys som resultat.


Subtraktiv fargeblanding
Den fargeblandingen vi vanligvis opplever skjer i forbindelse med at man fjerner farger (derfor ordet subtraktiv). Når vi legger nye farger oppå gamle vil hver farge fjerne noen farger og resultatet kan da bli nye farger. De nye fargene vil da alltid bli mørkere og dessuten vil de være nabofarger til de fargene som er brukt tidligere. De fleste vet vel at man får grønt om man blander blått og gult og at man ender opp med svart om man blander for mange farger. Figuren til høyre illustrerer subtraktiv fargeblanding og denne fargeblandingen forutsetter da hvitt lys som kommer fra en eller annen ytre lyskilde.
Et hvitt ark vil da ikke absorbere noen farger, men spre alle fargene tilbake like mye. Et svart ark vil på den andre siden absorbere alle fargene og ikke spre noen farger tilbake. Mellom disse ytterpunktene har vi da det meste av det vi ser omkring oss.

Se animasjon: Fargeblanding
Siden frekvensen til fiolett er nesten dobbelt så høy som frekvensen til rødt (tilsvarer en oktav i musikken), så vil de påvirke samme sansecellene i øyet og vi vil derfor se en gradvis overgang mellom rødt og fiolett. Derfor er det vanlig å fremstille fargene i en fargesirkel slik som vist til høyre. Denne er da nyttig når man skal forstå hvordan man kan blande farger.
Grunnprinsipp 1: Fargestoff fjerner farger
De fleste lyskildene vi omgir oss med sender ut tilnærmet hvitt lys som da består av alle farger. Når så gjenstanden som omgir oss har ulike farger så har det vanligvis sammenheng med at disse kun sprer tilbake noen farger. De andre fargene blir da absorbert. Når et blad er grønt så er altså årsaken at bladet absoberer de andre fargene og det er da i
hovedsak er det grønne lyset som sprees tilbake eller slipper gjennom bladet. Når vi maler med gult på et hvitt ark, så vil pigmentene i det gule fargestoffet absorbere alle farger bortsett fra gul.
Grunnprinsipp 2: Naturens filter har ikke skarpe grenser
Det å fjerne noe kalles ofte filtrering, og det som fjerner farger kan vi da kalle filter. I naturen er det da slik at de fargefilter som slipper gjennom noen farger og absorberer andre farger har en gradvis overgang mellom det som fjernes og det som slippes gjennom. Det betyr med andre ord at nabofargene (se fargesirkelen ovenfor) til den fargen som slipper gjennom, vil slippes delvis gjennom. I praksis betyr det at et gult fargestoff bare delvis vil fjerne grønt og orange lys. Det som er malt med et gult fargestoff vil se gult ut fordi den gule fargen da vil dominere over nabofargene grønt og orange, men disse fargene er ikke fjernet helt.


Tidligere har vi nevnt at hvitt lys kan gi fargespekter som følge av at lysfarten for ulike farger er ulik. Når vi ser farger i såpebobler, oljeflekker på vann, gitter, CD-plater ol. så er årsaken en annen enn den vi har forklart foran. Her vil vi da se nærmere på hva vi kan bruke ei CD-plate i forbindelse med undervisning om lys. Men her som ellers er det viktig at man forstår det man holder på med, og derfor vil vi her først forklarer begrepet interferens som er grunnleggende i mange ulike sammenhenger.
Interferens er ifølge leksikon samspill mellom to eller flere bølgebevegelser (av latin: inter=mellom ferire=støte mot hverandre). Her vil vi da videre påstå at dette begrepet ikke er så vanskelig som noen tror. Interferens er et sentralt fenomen i lyd, lys og havbølgeteori og tilsynelatende uforståelige observasjoner blir enkle å forstå om man forstår dette begrepet. En mulig grunn til at noen opplever at interferens er et vanskelig begrep er nok at de tenker at lys består av små uavhengige partikler som kalles fotoner. Dette er det rådende synet i universitetenes fysikkmiljø og ulike bøker påstår ofte at lys består av fotoner. Nå er det imidlertid et faktum at kvantemodellens fotonforklaring ikke er bevist (om noen sier noe annet så spør om du får se beviset). Videre er det et faktum at alle lysfenomen best kan forklares om vi antar at lys er bølger. Dette gjelder i særlig grad de fenomenene som har med interferens å gjøre, og her vil vi bare kort anbefale leseren å tenke at lys er bølger (ikke partikler).

Bølgetog En bølge vil alltid bestå av flere etterfølgende bølgetopper på samme måte som et tog består av mange etterfølgende vogner. Når det gjelder bølger vil vi videre se at en bølgetopp har mange likhetstrekk med en bølgedal (omsnudd men ellers samme form og størrelse). Et bølgetog vil altså bestå av mange etterfølgende bølgetopper med likeformede bølgedaler mellom og om man klarer å tenke på en lysstråle som et slikt bølgetog, så er det relativt lett å forklare det vi kaller interferens. Forutsetningen for at vi skal få interferens er at et bølgetog dele opp i to eller flere bølgetog. Denne oppdelingen kan f.eks. skje ved at lysbølgen treffer to nærliggende spalter. Litt av lyset går da gjennom hver sin spalt. Interferens er da det som skjer om slike adskilte bølgetog møtes igjen. En grunnleggende forutsetningen for at vi skal få interferens er nemlig at to bølger må være koherente (koherent=likeformet) og i naturen vil denne betingelsen bare være oppfylt om begge lysbølgene kommer fra samme lyskilde. Etter at lysbølgene er delt i to vil de så beveget seg uavhengig av hverandre og man kan da tenke seg at de tilbakelegger ulike veilengder slik at de blir mer eller mindre forskjøvet i forhold til hverandre når de møtes igjen.

Konstruktiv interferens kalles det når to koherente bølger møtes på en slik måte at bølgetoppene fra den ene bølgen treffer bølgetoppene fra den andre. Resultatet blir da at intensiteten eller bølgehøyden blir lik summen av de opprinnelige bølgene. Også når to uavhengige (ikke koherente) lysbølger møtes vil vi oppleve at intensiteten blir lik summen av de opprinnelige lysbølgene. De færreste har problemer med å forstå dette for det er det vi vanligvis opplever.
Destruktiv interferens kalles det når to (eller flere) koherente bølger (likeformede bølger) møtes på en slik måte at bølgetoppene fra den ene bølgen treffer bølgedalene fra den andre. Hvis vi summerer to slike bølger med lik amplitude vil vi få null og i praksis vil lyset forsvinner. Vi opplever med andre ord at to lysbølger som hver for seg inneholder energi vil utslukke hverandre når de kommer sammen igjen. Det er altså ikke snakk om at energien blir absorbert i et eller annet stoff og så langt har jeg ikke funnet at noen kan forklare hvor energien er blitt av ved en slik utslukning. Det er derfor mye som tyder på at energien har forsvunnet totalt selv om mange fysikere tror at energi ikke kan forsvinne. I ulike sammenhenger vil vi kunne observere mørke felt i lysstråler og i de fleste av disse tilfellene er disse en følge av destruktiv interferens.


Newtons ringer Det var Isaac Newton som først oppdaget fenomenet som vi i dag kaller destruktiv interferens, da han slipte linser til sine ulike optiske forsøk. Han oppdaget da at det oppstod noen mørke ringer om han la planslipte glass på hverandre. Dette fenomenet kan vi observere når vi bruker tynne dekkglass ved mikroskopering og i noen lysbilderammer med glass. Vi opplever det vanligvis ikke om vi legger to vanlige glassplater sammen, og årsaken er da at overflaten av vanlig glass er for ujevn. På lysbilderammer kan vi av og til finne begrepet 'anti-newton' og det forteller da at glassflatene er gjort litt ujevne slik at det ikke oppstår slike mørke ringer når man sette lysbilder i dem. Hvordan forklarer vi så årsaken til disse mørke ringene? Som vi har sett tidligere vil det skje en refleksjon både når lys går inn i glass og når det går ut av glass. Når så et glass ligger inntil ett annet glass vil to refleksjonsflater bli liggende svært nær hverandre og det kan da skje at det reflekterte lyset fra to slike nærliggende flater kommer sammen igjen på en slik måte at bølgetopper fra den ene strålen møter bølgedaler fra den andre. Dette vil skje om ekstraavstanden som den ene lysstrålen går i forhold til den andre er: s=½l, s=1½l, s=2½l osv. Siden bølgelengden til lys er mindre enn 1mm (mikrometer) så må avstanden mellom glassflatene være i denne størrelsordenen for at vi skal kunne observere Newtons ringer.
Farge i såpebobler og oljefilmer
Såpebobler og oljefilmer er svært tynne (i størrelsorden µm) og det vil derfor oppstå interferens mellom lys som treffer den fremre og bakre refleksjonsflaten. Det betyr da at vi kan forvente å få mørke ringer som følge av destruktiv interferens. Når vi i stedet ser fargeringer så har det sammenheng med at bølgelengden for de ulike fargene varierer endel. Bølgelengden for rødt lys er faktisk nesten dobbelt så lang som bølgelengden for fiolett lys og det betyr da at de ulike fargene vil bli utslukket ved ulike tilbakelagte avstander ifølge det som er nevnt ovenfor. Den eksraavstanden som lyset fra den bakre flaten har gått er videre avhengig av vinkelen som lysstrålene har i forhold til flata (liten vinkel => stor ekstraavstand), og resultatet blir at de ulike fargene får utslukning ved forskjellige vinkler. Det betyr igjen at vi vil se ulike farger ved ulike vinkler og det forklarer da hvorfor vi ser farger i såpebobler og oljefilmer. Det som kjennetegner interferenseksemplene som er nevnt så langt er da at delingen i to ulike stråler skjer i ei speilflate hvor noe lys reflekteres og resten av lyset ikke reflekteres.

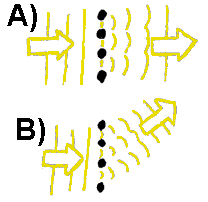
Fargespekter fra gitter
Et gitter er en samling av to eller flere smale gjennomsiktige spalter som deles opp av et tilsvarende antall smale ugjennomsiktige "gitterstenger". Gitteravstanden er avstanden mellom nabospalter/nabostenger og i optiske gitter er denne i størrelsorden µm. Det vil da si at gitteret er så smått at vi ikke kan se det. Ytre sett vil et gitter vanligvis se ut som en vanlig plastbit, men om vi sender lys gjennom det vil vi kunne skille ut hva som er gitter og hva som bare er vanlig plast. I et gitter vil vi se farger men i vanlig plast vil vi ikke se farger. Det er faktisk også mulig å beregne giteravstanden utfra det som skjer med lyset som går gjennom et gitter.
Når vi sender lysbølger mot et slikt gitter vil det dele bølgen opp i mange parallelle bølgetog som så får kontakt med hverandre på baksiden av gitteret. Se figur. Det normale er da at de bølgetoppene som hadde kontakt med hverandre før gitteret kobler seg sammen og får kontakt med hverandre på baksiden. I det lyset som fortsetter rett fram etter at det har gått gjennom et gitteret har nettopp dette skjedd. Hvis det opprinnelige lyset var hvitt vil også lyset på baksiden av gitteret være hvitt og det har tilsynelatende ikke skjedd noe spesielt med dette lyset. Hvis vi derimot ser litt ut til sidene for dette sterke lysmaksimumet vil vi kunne se ett eller fler mindre lysmaksima som da er betydelig svakere men til gjengjeld viser disse et fargespekter dersom det opprinnelige lyset var hvitt. Hvordan er det mulig å forklarer at noe lys har bøyd seg ut til sidene og i tillegg har dette lyset delt seg opp i et spektrum?
I noe bøker kan vi lese at lys går i rette linjer, men dette er da ikke helt sant. Sannheten er at lys vil bøyes omkring hjørner, men det er da snakk om så lite lys som bøyes, at vi til vanlig ikke vil se det fordi det lyset som går rett fram vi "overdøve" det som bøyes. Men hvis vi lager en tynn spalt ved å plassere to barberblad/tapetkniver tett inntil hverandre og lyser mellom dem med en pekerlaser vil vi kunne se at laserstrålen utvider seg på baksiden. Tilsynelatende trekkes lyset mot de to eggene og laserlyset blir da uttrekt på tvers av spalten (ikke på langs som det er nærliggende å tro). Grunnen til at vi ser denne bøyingen først når spalten blir smal er da at intensiteten i det lyset som går rett fram blir mindre når spalten er smal og da vil det bli lettere å se det lyset som bøyes. Men i praksis vil lys også bøyes omkring en enkelt egg, men det er da vanskelig å se dette. Et gitter består da av tusenvis av små spalter og lyset som slipper gjennom hver enkelt av disse vil da bli litt avbøyd til begge sidene og dermed spre seg ut i en vifteform på baksiden. Men hvorfor ser vi da ikke et bredt kontinuerlig lys bak et gitter på samme måte som vi så et slikt bredt lys bak "barberbladspalten"? Årsaken er interferens.


Interferens fra to spalter I prinsippet vil vi få samme resultat om gitteret har 2 eller 100 spalter, men her vil vi da forklare interferens ved å tenke på et gitter med to spalter. I begge spaltene vil det skje en bøying av lysstrålen og derfor vil lysbølgene spre seg ut i forskjellige retninger fra hver av spaltene. Vi kan da tegne bølgene fra en spalt som mange halvsirkler utenpå hverandre. Nedenfor følger et slikt bølgemønster som er ment å være en kopieringsorginal som da kan kopieres over til et lysark(transparent). Hvis vi så legger den kopierte transparenten over det opprinnelige mønsteret slik at sentrum i de to bølgemønstrene blir litt til side for hverandre, så vil vi se et karakteristisk mønster. I ei linje fra midtpunktet mellom spaltene og rett fram vil vi se at bølgetopper fra den ene spalten treffer bølgetopper fra den andre spalten. Det betyr konstruktiv interferens og det svarer da til det store lysmaksimaet uten farge som man alltid får rett fram bak et gitter. Til høyre og venstre for dette lysmaksimaet vil vi da se at vi får mørkere felt hvor en bølgetopp fra den ene spalten treffer en bølgedal fra den andre spalten. Dette betyr da destruktiv interferens og vi får da en utslukning av lyset i disse områdene. Vi får med andre ord et mørkt felt uten lys. Utenfor dette mørke feltet får vi da et nytt lysmaksima med konstruktiv interferens. Dette oppstår da som følge av at en bølgetopp fra en spalt møter foregående/etterfølgende bølgetopp fra den andre spalten.
(kopieringsmal bakerst i aktivitetsdokument)
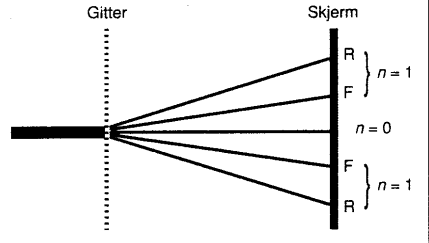
Årsaken til farger fra gitter I praktiske gitterforsøk vil vi se at alle lysmaksima bortsett fra det i midten (rett fram) består av et fargespekter hvor de enkelte fargene har skilt lag. Hvordan forklarer vi så dette? Generelt kan vi si at det lyset som møtes i de fargede lysmaksimaene har gått ulikt langt (en bølgetopp møter foregående eller etterfølgende bølgetopper), men det lyset som møtes i det store lysmaksimaet på midten har gått like langt (gangforskell=0). Betingelsen for at vi skal få konstruktiv interferens er da at gangforskjellen mellom de to strålene er en hel bølgelengde (eller 2 eller flere hele bølgelengder). Merk at bølgemønsteret som vi har brukt ovenfor har en bestemt bølgelengde (avstanden fra en ring til neste) og derfor svarer det til lys med en bestemt farge. I praksis så vil rødt lys ha nesten dobbelt så lang bølgelengde som fiolett lys. En måte å forklare hvorfor vi får fiolett lys nærmest det store lysmaksimaet er da at bølgelengden for fiolett lys er kortest. Det betyr da at gangforskjellen mellom de to strålene som skal oppnå konstruktiv interferens er kortest. Når det derimot gjelder rødt lys må gangforskjellen være nesten dobbelt så stor og derfor vil rødt lys få konstruktiv interferens lenger fra det store lysmaksimaet.

Lys er en viktig miljøfaktor i omgivelsene våre. I noen situasjoner kan det være aktuelt å beskrive det aktuelle lyset på en mer presis måte. Figuren til høyre viser de to parameterne som man vanligvis bruker i denne sammenhengen. Lys kan ha ulike frekvenser som øyet vårt oppfatter som ulike farger. Hvitt lys er da en sammensetning av de 7 grunnfargene som er vist her. De elektromagnetiske bølgene som har lavere frekvens enn det øyet kan oppfatte kalles infrarød stråling og i praksis er dette varmestråling som vi i visse situasjoner kan føle med varmefølsomme celle. Det er ellers mulig å lage såkalte varmefølsomme kamera som da kan ta bilder i mørket. De elektromagnetiske bølgene med høyere frekvens fiolett kalles ultrafiolett stråling og denne typen stråling er skadelig for mennesker. Heldigvis er det lite slik stråling på jorda siden atmosfæren absorberer hoveddelen. Vi har ingen celler på kroppen som kan føle slik stråling, men vi oppdager at vi har vært utsatt for slik stråling ved at hunden blir rød og senere utvikler pigmenter (solbrunhet) som hinderer at denne strålingen skal trenge inn i huden. I solariere og andre steder er det aktuelt å måle verdier for UV-stråling og da bruker man måleinstrument som er av samme typen som de vi nevner her, men disse har da filter som kun slipper gjennom UV-stråling (ikke vanlig lys).

Siden lys vanligvis vil blandes og sprees uten begrensninger, skiller det seg fra f.eks. ekeltronstrøm i en elektrisk ledning eller vannstrøm i en vannslange. I de to siste tilfellene vil strømmen langs hele ledningen være den samme og vi kan derfor koble oss inn hvor vi vil og måle en strømverdi. Når det derimot gjelder lys, så vil utsendt lys vanligvis være forskjellig fra mottatt lys og derfor opererer vi med to begrep når vi snakker om lysstyrke. Disse er utstråling og belysningstyrke. Siden vi vanligvis er mer interessert i virkningen av lyset enn av årsaken til lyset, så vil vi her konsentrere oss om belysningsstyrke som måles i lux. Figuren til høyre illustrerer forskjellen på Belysning (lux) og utstråling (lumen). Et eksempel som viser dette får vi om vi tenker på vanlige lyspærer på 40W og 60W. Ved et skrivebord vil en pære på 60W gi større belysningsstyrke/innstråling (lux) enn en på 40W under ellers like forhold. Grunnen er at vi vet at en pære på 60W har større utstråling enn en på 40W. Wattverdien til en pære sier da noe om total utstråling av energi fra pæra (egentlig tilført elektrisk energi). Merk at pæren sender ut både lys og varme og wattverdien forteller da hvor stor summen er. Wattverdien sier altså ikke noe direkte om hvor mye lys vi får fra ei pære, men det er opplagt at jo større wattverdien er, jo større er lysutstrålingen. Nå er det likevel mulig å få større innståling fra en pære på 40W om vi plasserer denne nærmere skrivepulten enn pæren på 60W. I dette tilfellet er utstrålingen mindre (mindre wattverdi) men innstrålingen (luksverdien) er større. Egentlig burde lysstyrken til lyspærer vært oppgitt i lumen, men siden det er vel så interessant for oss å vite hvor mye strøm ei pære bruker (det er den vi betaler for), så er det blitt vanlig å bruke W som verdi på ei lyspære. Etter at de såkalte sparepærene ble innført, har man av og til prøvd å oppgi en lumenverdi, men det vanligste er å si at de f.eks. lyser som ei 60W normalpære (med glødetråd), men at den f.eks. bruker en effekt på 11W (elektrisk effekt).

Generelt kan vil si at lysstyrke kan handle om både utstråling (fra f.eks. ei pære) eller belysning på f.eks. en arbeidsbenk eller ei bok. Her er det da det siste vi vil konsentrere oss om siden det er for at mennesker skal se at vi bruker lys i ulike sammenhenger. Det er derfor naturlig å knyttet belysningsstyrken opp mot det mennesklige øyet (Ikke katte-øyner eller andre som f.eks. ser bedre i mørket). Kurven til venstre viser hvordan øyets følsomhet varierer med frekvensen/bølgelengden av elektromagnetiske stråling (lys). Øyet er mest følsom for gult lys. Om vi setter følsomheten for gult lys lik 1 vil følsomheten for andre farger bli mellom 0 og 1 slik kurven viser. Denne kurven fungerer da som en kalibreringskurve som skal justere de måleinstrumentene vi bruker slik at ulike farger får ulik vekting. Målet er da en lux-verdi som svarer til det vi ser med øynene våre. Blått lys må f.eks. være relativt sett mye sterkere enn gult lys om øyet vårt skal synes at de to lyskildene er like sterke. Lux-verdiene skal da gjenspeile hva øynene ser og ikke de reelle energiverdiene i lyset.
Standardbenevningen for belysning er lux som er et utrykk for belysningsstyrke som vi her kaller lysstyrke. Det vil med andre ord si at den angir hvor mye lys som treffer et område. I forbindelse med installasjon av lys i offentlige bygninger (skoler ol.) er det visse krav til belysningsstyrke. I tabellen under vises noen eksempler på anbefalte verdier fra Selskap for Lyskultur. Statens Arbeidstilsyn bruker f.eks. disse. I skolen er det aktuelt å bruke lysmåler som gir lux-verdier. Disse er relativt rimelige og de kan gi elevene øving i systematiske miljømålinger.
Utendørs: |
Merk ellers at det er øyet vårt som er utgangspunktet for lux-skalaen og følgelig kan vi se ned mot 0 lux om natten. På den andre siden kan øyet tilpasse seg store lux-verdier og det har da ingen problemer med vanlig solskinn med luxvedier over 100 000 lux.


I skoleverket er det aktuelt å kunne måle noen verdier for lysstyrke, og et enkelt luxmeter som måler lysstyrke kan man kjøpe for en rimelig penge. Det er også mulig å lage enkle luxmeter, og fordelen med dette er da at man kanskje skjønner bedre hvordan de virker og hva slags problemer man får når man skal måle lysstyrke. Til høyre vises to luxmeter. Det som har en rød knapp og en kalibreringsskrue er et elder og dyrere instrument som kan måle luxverdier fra ca 5 lux til 2500 lux. Det andre er en billig-utgave til under 100 kr som har en relativt grov skala mellom ca 200 lux og 3000 lux. Felles for dem begge er ellers at de ikke trenger strøm fordi lyset selv sørger for nok strøm til å flytte på viseren.
Til venstre vises så et hjemmelaget instrument hvor en lysfølsom motstand slipper gjennom mer eller mindre strøm, og man finner da lux-verdien ved å vri på potensiometeret til de to lysdiodene lyser like mye. Pilen vil da peke på en verdi på underliggende papirark som da er kalibrert ved hjelp av en annen lysmåler. Denne lysmåleren kan da måle luxverdier mellom ca 10 lux og 500 lux. .


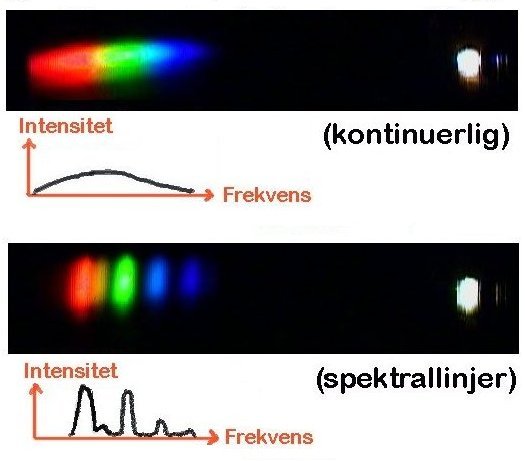
Instrumentene som er nevnt ovenfor er alle beregnet på å måle normalt hvitt lys som er sammensatt av ulike farger. Om vi i stedet ønsker å undersøke fargesammensetningen av lys, så er det snakk om å bruke et såkalt spektrometer. Et spektrometer kjennetegne av at de deler lyset opp i sine respektive farger slik at man kan finne det relative forholdet mellom ulike frekvenser i lyset. Oppdelingen av lys i ulike frekvenser kan skje ved å sende lyset gjennom et prisme eller et gitter. Dette er da omtalt tidligere. Når vi så studerer spekteret som fremkommer vil det vanligvis være enten et absorbsjonspekter eller et emisjonspekter. Vi får absorbsjonspekter når hvitt lys (eller andre "brede" strålinger) går gjennom en prøve. Det som kommer ut på baksiden er da det lyset som ikke er absorbert, og spekteret forteller da hva slags stråling som er blitt borte. Vi får emisjonspekter om vi tilfører energi til en prøve på en slik måte at den selv sender ut lys (eller andre typer stråling). I dette tilfellet viser da spektroskopet hvor mye av de ulike frekvensene det aktuelle stoffet sender ut. Et emisjonspekter kan enten være et bredt kontinuerlig spekter eller så kan det bestå av relativt smale topper med lite eller ingenting mellom. Slike smale topper i et emisjonspekter eller smale daler i et absorbsjonspekter kalles da spektrallinjer fordi de ser ut som linjer vertikale linjer i et diagram hvor vi avsetter frekvensen langs den horisontale aksen og intensiteten langs den vertikale aksen.
Ulike stoff vil sende ut ulike spektrallinjer når de blir inngår i kjemiske reaksjoner. Om vi kikker på flammen fra et stearinlys eller andre lyskilder som forbrenner vil vi vanligvis se et kontinuerlig spekter. Men om vi f.eks. dypper en ståltrådbit i vanlig kjøkkensalt eller andre kjemiske stoff og så varmer dette opp i en gassflamme vil vi se ulike farger som vanligvis består av bestemte spektrallinjer. Om vi tilsvarende stikker kobber inn i en gassflamme vil vi i starten se et grønnlig skjær som da er karakteristisk for kopperforbindelser. Ulike spektrallinjer er altså karakteristisk for ulike stoff. I analyse for å bestemme innholdet av ulike stoffprøver kan man da varme opp disse stoffene og fargespekteret som da fremkommer forteller da noe om hva slags stoff man har med å gjøre.
Spektralundersøkelser i grunnskolen
Spektrometer
er vanligvis dyre instrument som er vanskelig å bruke og det er derfor
ikke aktuelt å innføre spektralundersøkelser i grunnskolen.
Men enkle observasjoner som viser prinsippet for spektralanalyser er aktuelle.
Det kan f.eks. være aktuelt å bruke en CD-plate og observere forskjellen
på spekteret fra en vanlig glødelampe og en sparepære slik
som beskrevet i aktivitetsdelen. Her vises hva vi kan se sammen med en kurve.
Her er det viktig å forstå at kurva er en annen måte å uttrykke
det vi ser når vi ser farger. Et spekter er da et diagram hvor x-aksen viser frekvens/farge og y-aksen intensitet/belysningsstyrke.
En kurve i dette diagramment kan da fortelle hvordan de ulike fargene er sammensatt
i det vi til vanlig oppfatte som ett lys med en farge. I eksemplet
her ser vi på lys fra to pærer som tilsynelatende begge er hvite,
men spekteret viser da at lyset har ganske forskjellig sammensetning.
Litt om laser:
Skolelasere var tidligere helium-neon-typen som
krevde tilgang på strøm og har bølgelengde 630nm (rødfarget lys). I
dag er det lett å få kjøpt enkle små lasere som går
på batteri. Til skolebruk i vanlige klasserom er det passe med laser som gir en strålingseffekt på 1-3mW. For elevbruk anbefales ikke over 1,5mW.
De pekrlaserne vi har ved HVO har effekt 1mW. Man regner med at effekter under 15mW er ufarlige. Likevel bør man ikke nistirre rett inn i strålen
på samme måten som vi ikke må nistirre på sola. En laser som har liten bruk eldes hurtigere enn om den er noe i bruk. Man kan
gjerne la laseren lyse et helt døgn en gang per måned. Merk ellers
at en laser på 1mW gir fine røde markeringer på vegger og
tak innendørs, men om man vil ha en laser som man også kan bruke
som pekeinstrument utendørs, så trenger man større effekt.
Dagslyset vil med andre ord overdøve laserlyset om det er for lite effekt
i laseren.
I lærebøker for videregående skoler som tradisjonelt har vært brukt i lærerutdanningen er det vanlig å gi regneeksempler knyttet til fagstoffet og her vil vi da vise noen slike eksempler. I grunnskolen er det mindre aktuelt å regne på lysbrytning, men en lærer som skal undervise om lys bør likevel kjenne til formlene for bøying ved interferens og refraksjon (Snells brytningslov).

Hvordan
måle små avstander v.h.a. interferensmønster?
Her vil vi først vise
hvordan vi kan bruke enkle geometriske betraktninger for å beregne små
avstander. Hvis man f.eks. lurer på hvor tett sporene i en CD-plate ligger kan
vi finne denne avstanden ved å belyse plata med lys med en kjent bølgelengde.
Det røde lyset fra en pekerlaser er oppgitt til å ha en bølgelengde i
vakuum/luft på ca 640nm som da tilsvarer en frekvens på 468THz. Om vi sender
dette lyset inn mot en CD-plate slik figuren viser og måler vinkelen mellom
reflektert hovedstråle og første lysmaksima så finner vi en vinkel på ca 25°. I
figuren til høyre har vi tegnet en skisse som viser hovedstrålen ut (og inn),
første lysmaksima og vinkelen g=25° . Videre vet vi at i det første lysmaksimaet
har det ene bølgetoget gått en bølgelengde lenger/kortere enn nabobølgetoget og
vi kan da tegne en trekant hvor hypotenusen i trekanten svarer til avstanden
mellom to spor i CD-plata, og den minste kateten svarer til bølgelengden (l). Vi kaller da avstanden mellom sporene på CD-plata for d
og enkel geometri gir da følgende sammenheng:
sin(g)=l/d.
I vårt tilfelle er det d som er ukjent og vi kan da beregne avstanden mellom sporene på en CD-plate:
d=l/sin(g)=640nm/sin(25)=1,5mm
Snells brytningslov
I grunnskolen er det ikke aktuelt å regne med
de trigonometriske funksjonene (sin, cos, tg osv.) og følgelig er det mindre
aktuell å beregne avstander og vinkler ved hjelp av interferensformelen foran
eller brytningsloven som følger. Snells brytningslov er imidlertid vanlig i
mange lærebøker om optikk og lærere i grunnskolen bør derfor ha kjennskap til
den. Her følger da en innføring i denne loven.

Brytningsindeksen (n) er definert som forholdet mellom lyshastighetene i et medium og lyshastigheten i vakuum (n=c/v). Videre definerer man innfallsvinkel og brytningsvinkel (v) som vinklene mellom henholdsvis innfallende stråle og brudt stråle i forhold til innfallsloddet. Se figur. Når dette er definert kan man formulere følgende lovmessighet som kalles
Snells brytningslov: sin(v1)*n1=sin(v2)*n2
Merk at det er mulig å definere denne loven med andre rekkefølger av faktorer og også andre faktorer (eks: fart v i stedet for brytningsindeks n), og det som er vist ovenfor er da en av flere måter.
Oppgaveeksempel: Hva blir refleksjonsvinkelen om innfallsvinkelen er 45° og brytningsindeksen for glass er 1,5:
sin(v2)=sin(v1)*n1/n2
sin(v2)=sin(45°)*1/1,5=0,47
v=28°
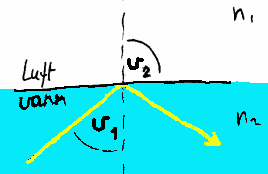
Totalrefleksjon
Utfra Snells brytningslov kan vi finne når man
får totalrefleksjon. Totalrefleksjon betyr at absolutt alt lys reflekteres i ei
flate. En måte å beskrive det på er å si at brytningsvinkelen er større eller
lik 90 grader (v2>=90° ) noe som da er umulig. Her er det ellers
viktig å merke seg at vi barer får totalrefleksjon når lyset møter en flate med
optisk mindre tett stoff (lavere brytningeindeks).
I endel sammenhenger er det aktuelt å finne grensevinkelen som gir totalrefleksjon og nedenfor vises et eksempel på når vi får totalrefleksjon i grenseflaten mellom vann og luft. I dette tilfellet vil vinkelen i luft være v2=90° og vi skal da finne v1. Brytningsindeksene i vann og luft er da henholdsvis 1,33 og 1,0 og vi får da:
sin(v1)*n1=sin(v2)*n2
sin(v1)*1,33=sin(90)*1
sin(v1)=1/1,33=0,75
v1=49°
Beregne linsestyrke.
I skolesammenheng oppgir man vanligvis linsestyke
med en såkalt fokusverdi som ofte har symbol f. Dette er da rett og slett avstanden
fra linsesenteret til brennpunktet i centimeter når linsa treffes av paralelle
stråler. I sollys er det da enkelt å måle fokusverdien til en samlelinse ved
hjelp av en linjal. I stedet for brennvidde eller fokusverdi
(f), bruker optikere en verdi som de kaller diopter (D). Sammenhengen mellom disse to er gitt av formlene:
f=100/D eller D=100/f.
Det betyr f.eks. at en linse med diopterverdi +1 har en fokusverdi på f=100/1=100. Det vil si at brennvidden er 1 meter.
Oppgaveeksempel:
Finn
brytningsindeks, grensevinkel for totalrefleksjon og brennvidde
a) Lag en
lysstråle ved hjelp av ei lyspære og en melkekartong med en spalt slik figuren
viser. Merk at lysstrålen må passere gjennom midtpunktet på den flate siden av
halvmåneglasset slik figuren viser. Bruk transpotør og mål innfallsvinkel og
brytningsvinkel vi= 45° og
vr= 29° .
Beregn
brytningsindeksen for pleksiglasset n = sin45 / sin29 = 1,47
b) Vri på halvmåneglasset slik at det akkurat blir totalrefleksjon.
Bruk transpotør og mål vinkelen ved totalrefleksjon:
vt = 43°
Beregn totalrefleksjonsvinkelen utfra den brytningsindeksen
ovenfor:
sinvt = sin90/1,47
=> vt = 43°
c)
Finn brennvidden til ulike linsemodeller (avkuttede linser)
Bruk
lyspære og melkekartong med 3 spalter og lag først parallelle stråler ved hjelp
av en konveks linse (samlelinse). La så disse strålene gå gjennom andre
linser.
Mål brennvidden v.h.a. linjal:
Brennvidde til konveks linse:
() f=6cm
Brennvidde til
halvmånelinse: (] f=5cm
Brennvidde til konkav linse: )(
f=7,5cm