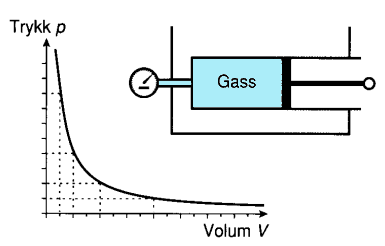
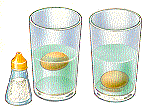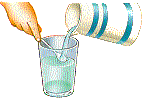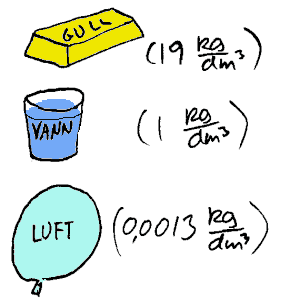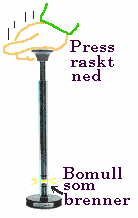Dette er en generell lovmessighet som ikke gjelder fullt ut i praktiske tilfeller.
Den er da relativt lite kjent og brukt og en grunn er kanskje at mange
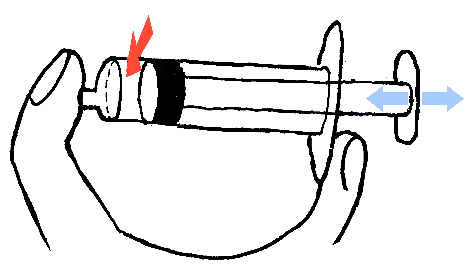
opplever den som selvfølgelig. Hvis vi f.eks. presser inn stempelet i en tett
engangssprøyte med luft i, vil volumet i engangssprøyten bli mindre samtidig
som trykket i luften øker. Det første ser vi og det andre kjenner vi ved at
vi stadig må trykke hardere for å få stempelet ytterligere inn.
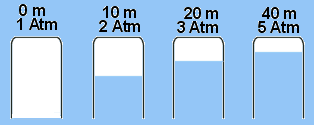
En annen måte å anskueliggjøre denne loven er å tenke seg at man tar med
seg litt luft i en dykkerklokke nedover i vann. På 10m hvor trykket er dobbelt
så stort som lufttrykket ved havoverflaten vil da luftvolumet bli halvdelen
så stort. Ved 20m hvor lufttrykket 3 ganger så stort som ved havoverflaten vil
luftvolumet bli 1/3 osv.
Gay-Lussac's lov
I 1802 oppdaget man at det også
var en lineær
sammenheng mellom trykk og temperatur (p=konstant·T). På den ene siden kan vi
da si at trykket vil øke når temperaturen øker om volumet er tilnærmet konstant).
Det er f.eks. det som skjer i en forbrenningsmotor (PSEp597).
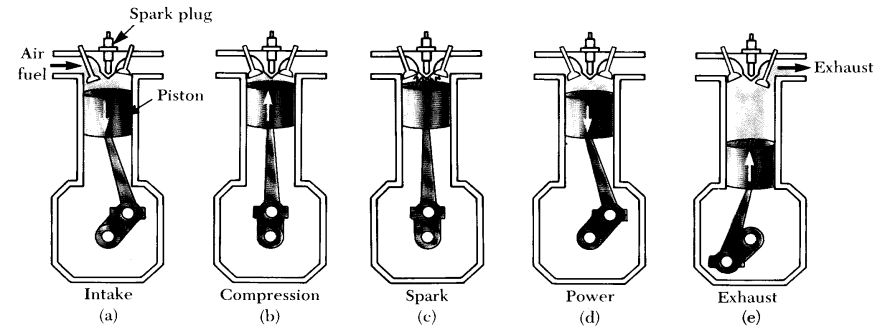 Firetaktsmotor a) innsuging b) kompresjon c) gnist
d) arbeid/kraft e) utblåsing
Firetaktsmotor a) innsuging b) kompresjon c) gnist
d) arbeid/kraft e) utblåsing
Om vi snur på formelen kan vi også si at økt trykk (f.eks. på grunn av sammenpressing) skaper økt temperatur. Dette kan vises ved såkalt
Adiabatisk fyrtøy som skaper så høy temperatur at en bommulsdott
tar fyr og brenner opp. Figuren
til høyre viser et gjennomsiktig rør
som er tett i enden og et stempel av metall som kan føres ned i røret.
Hvis man så plasserer en bit bommull øverst i røret og skyver
stempelet raskt ned med bommullen under, vil man kunne observere at det blir
så høy temperatur inni røret at bommullen brenner opp med
et kort lysglimt. Det er da dette prinsippet som forårsaker antenning
i en dieselmotor.
Om
vi holder fingeren foran hullet til ei sykkelpumpe mens vi pumper vil
vi kjenne at det blir varmt. Årsaken er at luft som presses sammen får
økt temperatur.
Så langt har vi nevnt eksempler på at økning i trykk eller temperatur
vil føre til økning i den andre verdien. Men det finnes også en annen sammenheng
mellom trykk og temperatur. Om vi reduserer trykket vil temperaturen avta, og
om vi reduserer temperaturen vil trykket avta. Når vi sprayer med en sprayboks vil sammenpresset
luft utvide seg når den slipper ut, og man får da en temperatursenkning. Det
er da dette prinsippet som brukes når temperaturen skal senkes i kjøleskap,
fryseboks og andre kjølemedier.
Tilstandslikningen for idealgass
De lovmessighetene som er beskrevet
ovenfor er i ettertid slått sammen til tilstandsligningen
for idealgass:
Denne likningen vil da fungerer som en slags grunnlov innenfor
gassfysikken, men det er da viktig å være klar over at den ikke gjelder 100%
i praktiske tilfeller. Derfor sier man ofte at den gjelder for en idealgass
(som da ikke finnes) og tilnærmet for andre gasser. I grunnskolen
er det sjeldent det er snakk om å bruke denne tilstandslikningen til å
finne konkrete verdier, men den er da nyttig som bakgrunn for å forklare hva
som skjer med de andre størrelsene i formelen ovenfor, når en av dem endres.
Merk
ellers at denne likningen bare handler om gass, og det er derfor ikke snakk
om en grunnlov i ordets egentlige forstand siden den ikke gjelder for væsker
og fast stoff
Daltons lov
Denne lovmessigheten er oppkalt etter John Dalton (1766-1844) og
den er da mindre kjent en tilstandslikningen. Den forteller da at man får en vanlig
summering av trykk (eller volum) når
man blander to ulike gasser. Det vil si at ulike gasser vekselvirker på samme
måte overfor like som ulike gassmolekyl. Det skjer da ikke en form for "stabling" når
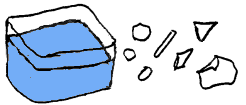
man blander molekyl med ulik form og størrelse. Når vi derimot blander salt
(fast stoff) og vann (væske) får vi et annet resultat. I eksemplet
som er vist til høyre vil volumet til saltblandingen blir mindre
enn hva vannvolumet og saltvolumet hver for seg skulle tilsi. (Gøy med
Vann s32)
Bernoulli's lov
Denne lovmessigheten er oppkalt etter sveitseren Daniel Bernoulli (1700-1782).
Den
forteller da at det er en sammenheng mellom hvor fort en gass strømmer
og hvor stort trykk man opplever. Denne er da slik at trykket avtar ved økende fart. Dette
er det motsatte av det vi intuitivt ville forvente og derfor forårsaker
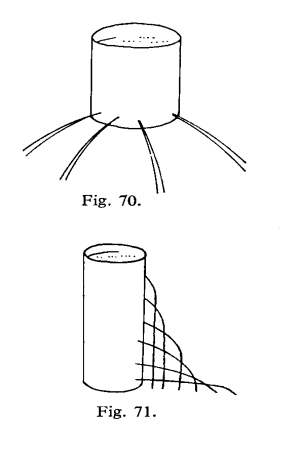
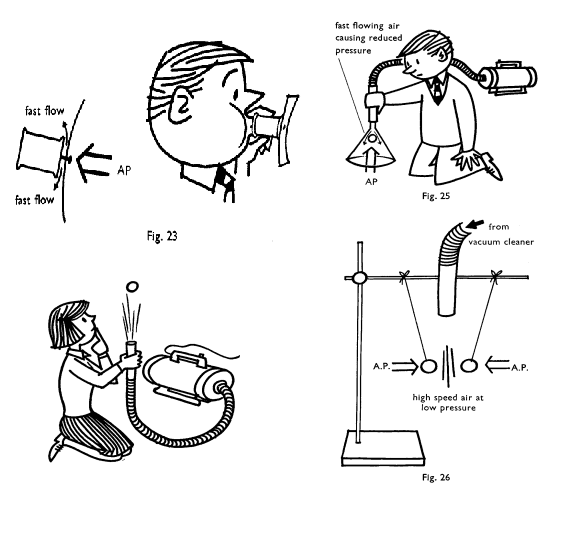
denne lovmessigheten endel "rare" situasjoner slik som vist på figurene
til venstre. Man skulle f.eks. tro at en papirbit foran hullet til ei trådsnelle
skulle blåse vekk når vi blåser fra andre enden. I de fleste tilfellene vil
ikke dette skje, og årsaken er da at luften som strømmer ut fra hullet og ut
mellom papiret og trådsnellen vil lage et undertrykk som holder papiret på plass
inntil trådsnellen.
Dette oppstår altså et slags sug eller undertrykk når farten til
en gasstrøm øker og dette kan da utnyttes på ulike måter. Prinsippet utnyttes i flyvinger, forgasser i motorer, sprøytepistoler
og mye annet. Dette er da
et eksempel på et fenomen som er vanskelig (umulig?) å forklare utfra kinetiske
partikkelmodell (kommer tilbake til den senere), men som da er lett og forklare
utfra em-modellen.
På samme måte som ordene tung/lett kan brukes om krefter
og massetetthet kan ordet varme brukes både om temperatur
og energi i dagligtale. Det er generell enighet om at man trenger å
skille mellom energibegrepet varme og begrepet temperatur, men det finnes da
ulike definisjoner av disse og det er da sannsynligvis årsaken til at
både barn og voksne har problemer med disse begrepene. I forbindelse med
undervisningen om disse begrepene i de første årene i grunnskolen
vil vi her foreslå følgende definisjoner:
Temperatur
er det vi måler med et termometer og som har benevning °C (grader
Celsius).
Varme er utrykk for energimengde og benevningen er J (joule).
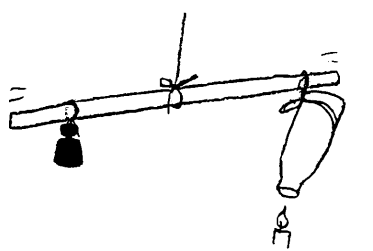
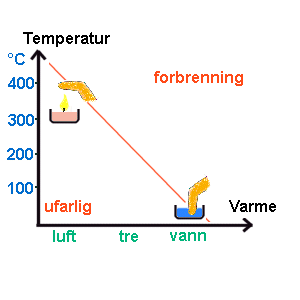
Figuren til høyre illustrerer forskjellen. Høy temperatur
er i seg selv ikke så farlig, om det er snakk om lite varme slik som f.eks.
i flammen/luften over et stearinlys. Det å føre fingeren over et stearinlys
er altså ikke farlig selv om temperaturen er noen hundre grader. På
den andre siden vil man relativt raskt få en farlig forbrenning om man
blir eksponert for vann med en temperatur på 60°C. Problemet
i dette tilfellet er ikke temperaturen i og for seg (kan f.eks. ha mye høyere
temperatur i ei badstu), men at det er snakk om mye energi som fører
til en rask oppvarming av en finger eller andre kroppsdeler. Vann har stor varmekapasitet
og følgelig inneholder det mye energi når det er varmet opp. Tilsvarende
er det også farlig å falle i kalt vann fordi energi/varme da vil
trekkes relativt fort ut av kroppen vår.

Termometer
som måler temperaturer
Temperatur er et grunnleggende begrep som
det er aktuelt å lære relativt små barn. I den sammenhengen
er det viktig å være konkret og å knytte begrepet opp mot praktiske
erfaringer. Siden temperatur er en kvantitativ verdi er det viktig at vi snakker
om temperaturverdier og lærer barna selv å finne temperaturverdier.
Det er f.eks. vanlig å lære barna relativt tidlig at vann fryser
til is ved 0°C og at temperaturen innendørs er ca 20 °C. Det
å bruke tall i forbindelse med temperatur er vanligvis ikke noe problem.
Temperatur kan derimot være et middel til å lære barn tall
samtidig som de innser at tall er nyttige til å beskrive den fysiske naturen
som omgir oss. Når det videre gjelder måling av temperatur finnes
det ulike termometer med ulik visning av temperaturen. Her vil vi understreke
at det ikke er noen selvfølge at barn kan bruke et termometer. Selv på
lærerskolen har vi f.eks. erfart at mange har problemer med å
finne hva som er aktuell temperatur, maksimuntemperatur og minimumstemperatur
på termometeret til høyre (max-min-termometer). Virkemåten
er ellers at søylene skyver på
de to løse pinnene når de bevegere seg oppover, mens pinnene blir
da ikke med ned igjen når søylene går nedover. Det er da en mangnet som hindrer pinnene
å gli ned. Når man så har lest av temperaturen trykker man
på knappen i midten og da vil avstanden mellom pinnene (vanligvis magnetisk)
og en jernplate på baksiden øke og pinne
glir ned. Temperaturmåling med max/min termometer er aktuelt i forbindelse med
værobservasjoner i grunnskolen.
Generelt kan vi si at temperaturen bestemmer hvor mye klær vi må
ha på oss. Videre har temperaturen en viss innvirkning på hvor fort
klær tørker. I denne sammenhengen kan man gjøre forsøk
med å plassere klær i ulike temperaturer og slik undersøke
sammenhengen mellom temperatur og tørketid.
Merk ellers at vind og luftfuktighet er to andre faktorer
som påvirker hvor mye klær vi må ha på oss og hvor fort
ting tørker. Det er f.eks. mulig å oppleve at ting tørker
fortere ute i vinden enn inne i varmen, men da er det viktig at læreren
understreker hovedregelen om at tørkingen går fortere jo høyere
temperaturen er under ellers like forhold.
Offisielle begrepsdefinisjoner:
Temperatur (latin:blande) - begrep som blir brukt til å beskrive følelsen av kaldt og varmt... I fysikken bruker man en gjenstands temperatur som et av begrepene til å beskrive tilstanden til gjenstanden eller stoffet i den... Alle stoffer sender ved alle temperaturer ut elektromagnetiske bølger som temperaturstråling... Ved stadig nedkjøling av et stoff skulle man kunne få en tilstand hvor molekylene ikke lenger er i bevegelse, et absolutt nullpunkt for temperatur.
Varme ...[ifølge teori] en form for energioverføring. Når to systemer med forskjellig temperatur er i kontakt med hverandre, vil molekylene i det ene systemet overføre noe av sin bevegelseenergi tiul molekylene i det andre systemet; det blir utført arbeid mellom molekylene. Det er dette molekylarbeidet som er varme. En annen form for varme er stråling...Lys ... Lyset viser etter kvanteteorien en dualitet. Det består av kvanter, fortoner oge er samtidig elektromagnetiske bølger. Dualiteten innebærer ikke noe selvmotsigelse, men er et uttrykk for at bilder vi henter fra dagliglivet er utilstrekkelige når det gjelder å beskrive naturens fundamentale egenskaper...(Store Norske leksikon)
Definisjonene her viser vel at det ikke er enkelt å finne en enkel og
forståelig definisjon av temperatur og varme. Her vil vi kort
si at definisjonen av temperatur som vi har valgt foran fungerer i forhold til
hva vi føler som kaldt og varmt, men den fungerer da ikke i forhold til
hvordan man vanligvis oppgir temperaturen i atmosfæren. Her påstår
vi altså at et vanlig termometer viser en temperatur som svarer til den
vi føler i huden, men det finnes da også en annen måte å
definere temperatur som gir helt andre temperaturverdier.
Dette har sammenheng med at man knytter temperaturen opp mot en tenkt gjennomsnittshastighet
til molekylene i luft/atmosfæren. Det er da den såkalte partikkelmodellen
som ligger til grunn for denne definisjonen og vi vil komme tilbake til dette
senere.
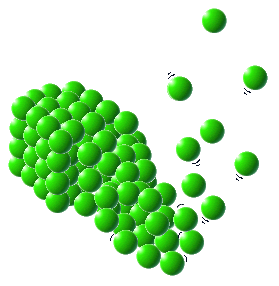
Temperatur og aggregattilstand
bestemmes av varmeenergi (prinsipp 1)
Alt som skjer på jorden er avhengig av energi, og her vil vi se litt nærmere
på den energiformen som vi kaller varme. Energi er noe som kan overføres fra
et sted til et annet og energiformen varme (også kalt indre energi) kan
da lagres på to måter:
1 Når vi tilfører energi til et stoff slik at temperaturen øker, så økes energien.
2
Når vi tilfører energi til et stoff slik at det går over fra fast stoff
til væske eller fra væske til gass så øker også energien.
Varme kommer fra ulike kilder
Vi trenger varmeenergi i ulike sammenhenger
og den kan vi få på ulike måter. Sola sender lys til jorda
og dette lyset blir da omdannet til varme. Vi erfarer f.eks. at en mørk
flate som sola skinner på, blir varm. I slike tilfeller vil lysenergi omdannes
til varmeenergi. Om vinteren har vi på våre breddegradere
lite sol, men det er likevel relativt varmt om vinteren i Norge. Endel av den
varmen vi har om vinteren blir da frigjort når vanndamp (som kommer fra
sør) blir omdannet
til skyer (vanndråper/væske) og eventuelt snø
(is/fast stoff). Dessuten kommer det endel varmt vann og endel varm luft fra
sør som da har med seg varneenergi.
Forsøk som viser relativ energimengde i temperaturforskjeller og aggregattilstander
For
å få et bilde av hvor mye energi det er snakk om i disse ulike tilfellene er
det vanlig å gjøre følgende forsøk:
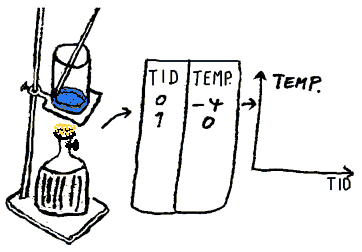
Utstyr: glasskar, snø, termometer og varmekilde(gassflaske).
Sett varmekilden under glasskaret og termometeret oppi. Les av temperaturen med faste tidsintervall inntil alt vann er fordampet. Lag en grafisk fremstilling av resultatet. Forklar den karakteristiske kurva som fremkommer.
Kurven forteller da noe om varmekapasitet til vann samt hvor mye energi som
"ligger i" overgangene is/vann og vann/vanndamp.
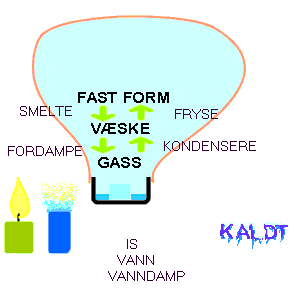
Som nevnt trenges det energi eller varme for å omforme
faste stoffer til væske (smelte is) og å omforme væsker til
gass (fordampe vann). Den energien man putter inn når vi smelter is og
fordamper vann kan vi da få tilbake når damp kondenseres og når
vann fryser.
Merk at alle stoff kan opptre i flere aggregattilstander Det er da i overgangen mellom to aggregattilstander at energiforskjellene er størst. Det er med andre ord disse overgangene som binder/frigjør mest energi. Det betyr f.eks. at det vil gå mye lenger tid før et kjøleelement som inneholder is blir varmt, enn et som bare inneholder vann, selv om de begge har en utgangstemperatur på 0°
C. Om kjøleelementet har en utgangstemperatur på -20°
C eller 0°
C gir en mindre energiforskjell enn den som er mellom is og vann. Først når vi har endret temperaturen i vannet/isen med 80°
C har vi tilsvarende energiforskjeller som vi finner mellom vann og is ved samme temperatur (0°
C). Når det gjelder fordampning av vann, vil energien som trenges for å fordampe en liter vann være ca 7 ganger så stor som den energien som går med til å smelte 1 kg is.
Se figuren til høyre hvor de grønne søylene viser hvor
mye energi som er involvert i de ulike omdanningene/temperaturendingnene. Dette viser at det "ligger" mye energi i overgangen mellom is, vann og damp. Dette "energilageret" er viktig for klimaet på jorda.
En måte å beskytte et vannrør mot frost
er f.eks. å sette en bøtte med vann i nærheten. Om vannet i bøtta
fryser først, vil den avgi varme helt til den er bunnfrosset og denne
varmen vil da beskytte vannrøret.
Det vi har nevnt så langt kan vi kalle fysisk lagring av energi, i motsetning
til kjemisk lagring av energi. For å få fram hvordan denne formen for energilagring
fungerer i naturen vil vi kort sammenlikne denne med naturens viktigste kjemiske
lagringsmåte for energi:
Kjemisk omforming av stoff
Kjemisk omdanning av stoff betyr at
stoffene forandrer kjemisk sammensetting. Det vanligste eksemplet er såkalt
forbrenning som skjer både i kroppen vår, i stearinlys og
vedovn. Det er viktig at elevene i grunnskolen skjønner forskjellen på
kjemisk og fysisk omforming av stoff, og her vil vi bruke et stearinlys som
eksempel for å illustrerer denne forskjellen. Når et stearinlys
brenner vil stoffet stearin forsvinne og vi får i stedet dannet gassene
vanndamp(H2O) og karbondioksid ( CO2). For at denne kjemiske
reaksjonen skal foregå må det da i tillegg tilføres oksygen(O2).
Den kjemiske formelen for denne omdanningen er:
Til sammenlikning vil en kjemisk formel for fordamping av vann være:
Ved en forbrenning får vi alltid ut energi i form av varme. Hvis vi
omdanner vanndamp til vann så får vi også ut energi. Det skjer
altså energiutveksling med omgivelsene både når vi har kjemiske
omforminger og fysiske omforminger. Det som skjer i figuren til høyre
kan beskrives ved hjelp av stoff-formler og energi-formler
slik som vist til under. Animasjon: Kjemisk og fysisk lagring av energi
|
CO2+H2O
-> karbohydrater+O2
lys
-> kjemisk energi
(fotosyntese)
|
karbohydrater+O2
-> CO2+H2O
kjemisk
energi -> lys+varme
(forbrenning)
|
H2O
-> H2O
varme -> indre
energi
(fordamping)
|
H2O
-> H2O
indre energi
-> varme
(kondenseing)
|
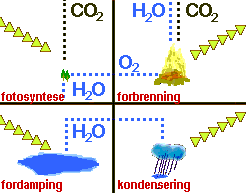
Figuren og tabellen viser at fotsyntese og fordamping krever energi i form
av lys og varme, mens forbrenning og kondensering avgir den samme energien som
lys og varme. Både når det gjelder energiomdanning og stoffomdanningen,
så kan vi betrakte prosessene til høyre som motsatte av de som
er til venstre.
Konserveringsprinsipp som gjelder for fysisk og kjemisk omdanning:
-
Det kommer like mye stoff ut av prosessen som det som gikk inn i den motsatte
prosessen
- Det kommer
like mye energi ut av prosessen som det som gikk inn i den motsatte prosessen
|
Termofysikkens hovedsetninger
En lærer som skal undervise om temperatur-relaterte emner bør kjenne
til termofysikkens hovedsetninger og derfor følger det her en kort kvalitativ
beskrivelse av hva den handler om. Generelt kan vi si at termofysikk i hovedsak
består av matematiske uttrykk og formler, men da disse er mindre relevante i
forhold til grunnskolen, har vi her vektlagt den kvantitative siden.
Termofysikkens 1. hovedsetning (energiloven)
Den første hovedsetningen i termofysikken, ofte kalt energiloven, fungerer
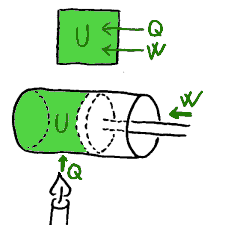
som en slags grunnlov når det gjelder energiomdanning. Ser vi på et avgrenset system, kan det utveksle varme Q og arbeid W med omgivelsene. Et avgrenset system kan i prinsippet være hva som helst. I en sammenheng kan det være aktuelt å tenke på solsystemet som et avgrenset system. I et annet tilfelle kan det være aktuelt å tenke på brennkammeret i en bensinmotor som et avgrenset system. Resultatet av den ovennevnte utvekslingen av energi med omgivelsene blir da en forandring i indre energi i systemet ΔU. Det som er nevnt her er egentlig en selvfølgelighet. Når dette er opphøyet til å kalles termodynamikkens første hovedsetning, så har det sammenheng med at den aktuelle formelen er grunnleggende i svært mange sammenhenger. Her følger termofysikkens første hovedsetningen formulert med ord og symboler:
Merk at tegnet Δ som er den greske bokstaven 'delta', betyr 'forandring' eller 'endring'. I dette tilfellet kan vi lese ΔU som 'forandring i indre energi'. Utfra denne lovmessigheten vil vi kort trekke ut en lovmessighet som er grunnleggende
i energisammenheng. Om systemet ikke har noen utveksling med omgivelsene, er høgresida i formelen ovenfor lik null. Da er også venstresida lik null. Et slikt system kalles et lukket system fordi det ikke utveksles noe med omgivelsene. Et spesialtilfelle av lovmessigheten ovenfor er da:

Et
lukket system har ingen utveksling av energi med omgivelsene
Energien i et lukket system er konstant. Det vil si at energi ikke kan skapes eller forsvinne, bare flyttes og omformes.
For oss betyr det at energien i universet, som vi regner som et lukket system, kan omdannes og forflyttes mellom ulike steder, men aldri forsvinne eller skapes. Et åpent system vil kunne motta eller miste energi. Et eksempel på et åpent system er jorda. Vi mottar energi fra sola og mister energi ut i universet i form av varmestråling. På jorda vil vi i praksis aldri ha et fullstendig lukket system, men ofte er det nyttig å tenke på områder som et tilnærmet lukket system.
Merk at energiloven ikke er bevist utfra vanlige vitenskapelige kriterier,
men alle forsøk tyder på at den i det minste er tilnærmet
rett. Den er også pedagogisk nyttig. Energiomdanninger blir relativt enkle
om vi kan anta at ingenting forsvinner og ingenting skapes i de aktuelle prosessene.
Om det da likevel skulle være slik at noe energi forsvinner i visse tilfeller,
så er det da vanlig å forklare slike tilfeller med at vi ikke har
et 100% lukket system, og det er derfor vanskelig å bevise noe annet i denne
sammenhengen.
Termofysikkens andre hovedsetning (entropiloven)
Denne hovedsetningen ble først formulert i 1856 av tyskeren Clausius. Her
kaller vi hovedsetningen for entropiloven. Også denne handler om noe som de fleste opplever som innlysende. Problemet er imidlertid at den naturloven som setningen peker på er forholdsvis vanskelig å beskrive eksakt ved hjelp av matematiske begrep. Generelt kan vi kanskje si at alle kjenner denne
loven, men få forstår de forholdsvis vanskelige beskrivelsene. Dette er nok en av grunnene til at de fleste lærebøkene i grunnskole og videregående skole har gitt denne hovedsetningen lite eller ingen plass.
I universitetslitteratur kan vi f.eks. finne følgene generelle formulering med ord og symbol:
Her er ΔQ endring i indre energi og T temperatur, mens ΔS er endring i entropien. Definisjonen ovenfor er vanskelig, og vi
vil derfor ikke vektlegge den her. Bakgrunnen for å ta den med her er at leseren skal ha sett den vitenskapelige måten å beskrive entropiloven, slik at man kan gjenkjenne den om
den dukker opp i en eller annen sammenheng. Det er da ikke aktuelt å bruke entropiloven på
denne formen i grunnskolen.
Et "kjøkkeneksempel" på bruk av den ovennevnte "universitertsversjonen": Om noen føler at det er vanskelig å forlate en formel uten å forstå prinsippet, vil vi kort prøve å anvende den på en kaffekopp med varm kaffe. Vi kaller da indre energi i kaffekoppen for Q1 og varmen i rommet for Q2. Tilsvarende blir temperaturen i kaffen T1 og temperaturen i rommet T2. I dette tilfellet vil energi forflytte seg fra kaffekoppen til rommet (fra høy til lav temperatur). Når vi skal beregne enropiendringen kan vi tenke oss et mellomområde som energien er innom på sin vei fra kopp til omgivelser. Så beregne entropien for dette. Årsaken er at vi får problemer med fortegnene om vi konsentrere oss om
kun to områder. Entropiendringen for dette området blir da:
Nå vil temperaturene endre seg som følge av energiovergangen, og derfor ser vi her på en så liten energiovergang at vi kan regne temperaturene for konstant. Rommet vil motta like mye energi som kaffekoppen avgir og derfor er ΔQ1 og ΔQ2 like store. Følgende forenkling viser at uttrykket må være positivt totalt sett siden T2 < T1 :
ΔS = ΔQ/T1 - ΔQ/T2 = ΔQ(1/T1 - 1/T2) > 0
Den fysiske grunnen til at uttrykket er positivt er da rett og slett vår påstand om at energi vil flytte seg fra den varme koppen til det relativt kaldere rommet. Disse kompliserte uttrykkene er da en måte å tallfeste erfaringer om at varme strømmer fra områder med høy temperatur til områder med lav temperatur og ikke omvendt.
Exergi
og anergi
I bøker for videregående skoler kan vi av og til
lese om begrepene exergi og anergi. Exergi er da definert som brukbar energi og anergi er definert som ubrukbar energi. En alternativ formulering av entropiloven vil da bli:
Energi kan omdannes til exergi og anergi. Forholdet mellom exergi og tilført energi vil være mindre eller lik 1.
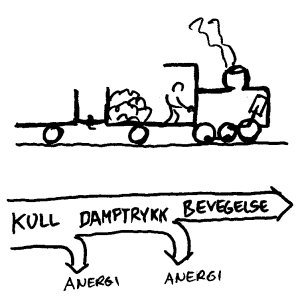
Det viktige i forbindelse med entropiloven er å forstå prinsippet. En vanlig illustrasjon er et damplokomotiv. Her vil energi i kull omdannes til energi i vanndamp som igjen omdannes til bevegelse-energi for toget. I hver av disse prosessene vil eksergien (den brukbare delen av den opprinnelige energien som blir overført til neste energiform i rekken være mindre enn den vi startet med. Endel energi går tapt i form av varmetap til omgivelsene (anergi). Over er
en figur som illustrerer hvordan den brukbare delen av energien (exergien) stadig blir mindre. Årsaken er at hver omdanningsprosess resulterer i ubrukbar energi som vi kan regne som tap.

Hva bør vi si om entropiloven i grunnskolen?
Generelt er vel entropibegrepet så vanskelig at vi ikke kan regne med at elever i grunnskolen skal få en fullstendig forståelse av hva det dreier seg om. Et problem er at det er så generelt og altomfattende at det er vanskelig å "peke" på det. Dette betyr imidlertid ikke at vi bør gi opp å snakke om entropiprinsippet i grunnskolen. Mange prinsipp
i denne lovmessigheten er åpenbare, også for elevene, og siden det er i grunnskolen at vi legger grunnlaget for forståelsen av naturen, er det viktig at elevene får hjelp til å trekke rette konklusjoner i en perioden hvor de uansett vil trekke endel konklusjoner. Om vi lar være å snakke om entropiloven, er det mye som tyder på at elevene vil trekker den konklusjonen at det som har med energi å gjøre er så vanskelig at de ikke vil forstå det uansett. Kanskje lager de seg også egne såkalte "hverdagsforestillinger" som kan gjøre dem "immune" mot "rett læring" på et senere tidspunkt. Her vil vi foreslå at vi bruker eksempler og såkalte "liknelser"
eller bilder når vi snakker om entropi. Liknelser er da historie eller beskrivelser av ting som ikke er entropi, men som likner på entropi. Her følger noen liknelser og eksempler som forhåpentligvis vil hjelpe å forstå entropiloven. Håpet er da at entropiloven skal få en litt større plass i grunnskolen enn den har i dag.
Det er vanskelig å lage en kort, eksakt og forståelig formulering av termofysikkens andre hovedsetning. Derfor vil vi her bruke litt tid på å beskrive noen eksempler hvor denne hovedsetningen gjelder. Håpet er at leseren skal oppdage det som er felles. Det generelle entropibegrepet synes også å gjelde i andre sammenhenger, og vi vil til slutt kort filosofere litt over hvordan entropibegrepet kan anskueliggjøres med eksempler fra områder som ikke er direkte tilknyttet energibegrepet.
Liknelse 1
Begrepet entropi kan best oversettes med ordet 'uorden' og vi får da følgende
generelle formulering som gjelder alltid:
Hva forstår vi med orden/uorden? I skolesituasjonen kan det være nyttig å snakke om uorden i stedet for entropi. Her er det imidlertid viktig å være klar over at vi kan mene ulike ting med ordet 'uorden'. Et nyttig prinsipp er å vurdere graden av uorden i forhold til den nødvendige oppryddingsprosessen som trenges. Målet for oppryddingsprosessen kan imidlertid variere "etter øynene som ser". Et eksempel: Er det mest orden i en boks med blandet krydder eller i bokser som bare inneholder ett krydder i hver? Hvis vi i dette tilfelle tenker på hvilke "oppryddingsarbeid" som er enklest, så er det klart at det er enklere å blande krydder enn å skille dem. Derfor vil vi som en hovedregel si at det er mer orden når ting er skilt eller når de er blandet. Uordenen øker altså når vi blander.
I de tilfellene vi har noe (A) som ugjenkallelig omdannes til noe annet (B), så vil maksimal uorden være når vi ikke har noe mer å omdanne (bare B) uansett intern
fysisk plassering. Et eksempel. Noen vil kanskje kalle det for maksimal uorden om vi blander løskruttpatroner ("rødfis") som er brukt og som ikke er brukt. Siden det er lettere å bruke løskruttpatroner (skyte med dem) enn "å gjøre dem ubrukt", vil vi her si at vi har maksimal uorden når vi bare har brukte patroner igjen. Husk at det er hvor vanskelig "oppryddingsarbeidet" er som avgjør graden av uorden, og ikke hva vi føler som mest ryddig.
Liknelse 2
Varme ting vil varme opp kalde ting. Når vi setter ei
gryte på ei varm kokeplate, vil det i utgangspunktet være en viss orden i og med at kokeplata er varm og gryta er kald. Atomene med høy termisk energi er altså samlet i kokeplata. Med tiden vil imidlertid atomene i kokeplata overføre energi til gryta. Etter ei stund vil vi finne molekyler med høy termisk energi jevnt fordelt i kokeplata og gryta. Ordenen har da avtatt og entropien har økt. Dette eksempelet handler om orden mellom atom/molekyl med hensyn på energien til de enkelte atom/molekyl. Dette viser at energifordelingen mellom stoff har noe å gjøre med ordenen til atomene/molekylene.
Med bakgrunn i det som er sagt så langt kan vi også formulere entropiloven
på følgende måte:
Varme (energi) vil gå fra steder med høyere
temperatur til steder med lavere temperatur (ikke omvendt)
Kan kalde ting varme opp varme ting? Ifølge
lovformuleringen ovenfor vil dette ikke kunne skje. Men hva er det så som
skjer i varmepumpe og kjøleskap? Alle vet for eksempel at stuetemperaturen (ca 20 °
C) ikke vil kunne varme opp en kasserolle med vann til kokepunktet selv om det i og for seg er nok energi til stede. Men
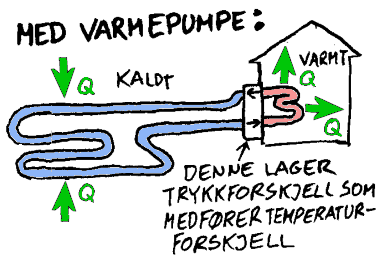
ei varmepumpe er tilsynelatende et unntak fra denne regelen. Varmepumpa er en tekniske konstruksjoner som lokalt kan overføre energi fra et relativt kaldt sted til et varmere sted. Hvordan er så dette mulig? I praksis viser det seg at entropiloven følges i alle deler av varmepumpesystemet isolert sett. Det er imidlertid lagt inn en trykkforskjell i det sirkulerende stoffet som gjør at dette endrer temperatur uten at vi tilfører varme. Vi endrer altså temperaturen ved hjelp av arbeid (W). Tidligere
har vi nevnt at temperaturen vil øke om trykket øker og et eksempel
på dette er når vi bruker håndpumpe og pumper opp sykkelen.
Vi kjenner at pumpa blir varm og det skyldes sammenpressingen av luft. Et annet
eksempel er adiabatisk fyrtøy som er nevnt i forbindelse med Gay-Lussac's
lov tidligere i heftet. Tilsvarende vil en reduksjon av trykk føre
til at temperaturen avtar. Et eksempel på dette får man når
man slipper ut gass fra gassflasker eller spraybokser. Vi kjenner da at det
blir kaldt. I ei varmepumpe er det da ei pumpe og en ventil (i "kasse"
som er festet til huset på figuren til venstre) som sørger
for ulik trykk og dermed også ulik temperatur på to forskjellige
steder. Begge disse stedene vil det da overføres varme fra varme til
kalde områder slik som entropiloven ovenfor sier. (denne varmen er markert med
grønne piler på figuren til venstre). Poenget
er da at pumpesystemet gjør at det som er inni rørsystemet på
utsiden av huset er kaldere enn omgivelsene og dermed vil omgivelsene avgi varme
til væsken inni rørsystemet. Man har så videre valgt å
fylle rørsystemet med et stoff som har kokepunkt lavere enn omgivelsestemperaturen
og det betyr da at energien fra omgivelsene går med til å fordampe
vesken slik at den blir omdannet til gass (dette skjer i det blå området). Denne prosessen innebærer opptak
av endel energi som så frigjøres igjen når gassen går
over fra gass til væske i rørsystemet inni huset (dette skjer i det røde området).
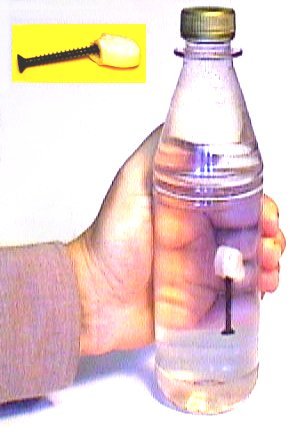
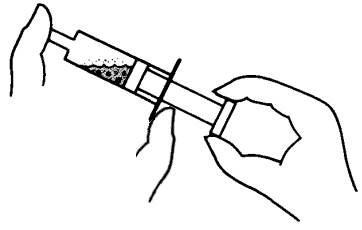
Om vi fyller
litt varmt vann (ca 50°C) i en engangsprøyte og reduserer trykket
slik som figuren til høyre viser, vil vi se at vannet begynner å
koke selv om temperaturen er langt lavere enn 100°C. Dette er da et enkelt
demonstrasjonsforsøk som viser at væsker kan koke/fordampe ved
ulike temperaturer avhengig av trykket og det er da dette prinsippet som utnyttes
i ei varmepumpe og et kjøleskap.
Liknelse 3
Merk at entropien vil øke både globalt og i de enkelte detaljene i varmepumpa. Derfor representerer ikke varmepumpa et brudd med entropiloven. Når varmepumpa tilsynelatende representerer et brudd med formuleringen: "energi vil alltid gå fra område med høy temperatur til områder med lav temperatur", så kan vel dette enklest beskrives som at teknologi kan minke entropien lokalt
på bekostning av en større global økning av entropien.
Her følger
så en liknelse som illustrerer et slikt "lokalt lovbrudd": Ei elv vil naturlig dra en robåt med seg nedover mot havet. Loven her er at alt vann og alt som flyter på elva vil sakte men sikkert bevege seg nedover elva. Hvis så personen i robåten begynner å ro oppover elva, vil det at båten beveger seg oppover være et tilsynelatende brudd på loven om at alt skal bevege seg nedover. Dette bruddet får vi om vi kun konsentrerer oss om båten og ikke ser på båten og elva som en helhet. Bakgrunnen for at vi klarer å ro oppover ei elv er at vi med årene sender noe vann raskere enn normalt nedover elva. I sum vil altså det vannet som årene påvirker og båten selv, bevege seg nedover elva som "naturloven" ovenfor tilsier. Det at vi ror oppover elva har altså den "prisen" at noe vann kommer raskere til havet. Tilsvarende vil også ei varmepumpe føre til at "nedoverprosessen" går fortere andre steder, og totalt sett er også varmepumpa underlagt entropiloven.

Liknelse 4
Energikvalitet
Ved kan brenne og i denne prosessen omdannes kjemisk energi i veden til varmeenergi. Vi opplever imidlertid aldri at denne prosessen reverseres eller snus slik at det dannes ved av varm røk. Naturen inneholder altså irreversible prosesser eller enveisprosesser. I praksis vil vi finne at energiformene ofte følger faste mønster når de omdannes. Når vi har bruk for energi i ulike sammenhenger, er det ikke alle energiformer som er like anvendelige. Det er med andre ord visse energiformer som er lettere å omdanne til den energiformen vi ønsker enn andre. På bakgrunn av erfaringer med hva som lettest omdannes til hva, kan vi derfor
snakke om energikvalitet og rangere energiformene i et slags kvalitethiraki. Et
mulig slikt hirarki er vist til høyre.
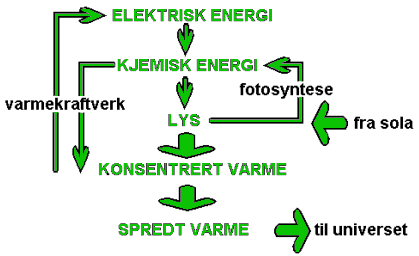
Den generelle tendensen er da at den naturlige energiomformingen vil foregå nedover i skjemaet slik som de
korte og brede pilene viser. Fra sola får vi tilført ny energi i form av lys. Jorda vil i sin tur sende ut varme til universet. Om vi skal prøve å samle det i en generell lovmessighet kan vi kanskje si følgende:
Vanlige energiomforminger vil gi lavere energikvalitet som resultat
Energien vi mottar fra sola vil vanligvis omdannes til varme. Ved kan brenne og gi lys og varme. Sluttresultatet etter en eller flere omdanninger blir alltid varme. Når varmen er blitt tilstrekkelig spredt, er den også ubrukelig til å omdannes til andre energiformer. Nå er det
som er vist ovenfor et generelt skjema og det kan finnes unntak.
I skjemaet ovenfor har vi vist to eksempler hvor energiomformingen skjer
oppover eller "mot strømmen". I denne sammenhengen representerer fotosyntesen i plantene og ulike former for elektrisitetsverk et unntak fra den "vanlige" omdanningen av energi. Det som kjennetegner de prosessene som omdanner energi "mot strømmen" er teknologi. Her brukte vi ordet teknologi på en generell måte som også innbefatter prosessene i biologiske organismer. Et kjennetegn på kompliserte teknologiske innretninger er at de ikke oppstår spontant av seg selv. Generelt kan vi vel si at de enten er et resultat av et biologisk frø eller menneskelig intelligens. En mulig tilføyelse til regelen ovenfor kan derfor være:
Teknologi kan omdanne mindre energimengder "mot strømmen" fra lav til høy kvalitet.
Det andre eksemplet på energiomdanning "mot strømmen" er det vi
ovenfor har kalt varmekraftverk. I et varmekraftverk blir kjemisk energi omdannet
til elektrisk energi, og i praksis skjer dette ved at den kjemiske energien
blir omdannet til konsentrert varme i en forbrenning som så i neste omgang driver
en generator som lager strøm eller elektrisk energi.
Termoelement Varmepumpen
som er beskrevet ovenfor vil øker
temperaturforskjeller når vi tilfører litt elektrisk strøm.
Et termoelement av den typen som finnes i en kjølebag som kan kobles
til sigarettenneren i en bil fungerer da etter samme prinsippet. Om vi kjører
likestrøm in på de to ledningene på peltierelementet/termoelementet
som er vist til høyre vil den ene siden bli varm mens den andre
siden blir kald. Mens et vanlig kjøleskap alltid blir kaldere inni enn utenfor,
vil da en kjølebag som inneholder et termoelement kunne fungere både som et
kjøleskap og som et varmeskap. Omkoblingen mellom disse to funksjonene består
da i at man snur strømmen gjennom termoelementet.

Men et slikt termoelement kan også brukes på en
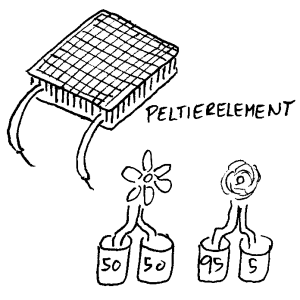
annen måte. Et glass med kaldt vann og et glass med varmt vann har i seg selv muligheter til å gi oss elektrisk energi. Til skolen er det mulig å kjøpe en såkalt termoelektrisk omformer eller peltier-element. Dette
er da det samme som vi ovenfor har kalt termoelement. Ved å tilføre ulik temperatur til to sider av et peltier-element kan vi få ut elektrisk strøm som kan drive en elektromotor. Forutsetningen er at det er en tempraturforskjell til stede. Jo større temperaturforskjell, jo mer strøm. I
figuren over
er det skissert et slikt forsøk. Det er altså mer orden (mindre entropi) i ett glass som har temperatur 5°
C og et som har 95°
C enn to som har samme temperatur. Hvis glassene med ulik temperatur tømmes sammen eller hvis de bare står vil muligheten for å hente ut energi forsvinne. I denne sammenhengen betyr lik temperatur maksimal entropi. Hverken i Sahara eller på Sydpolen er det gode forhold for slike termoelement. Årsaken er at temperaturforskjellen mangler. Om det derimot er et sted hvor varme møter kulde, vil vi kunne få ut energi i form av vind, strøm eller andre energiformer. Sterke stormer oppstår f.eks. der hvor varm og kald luft møtes.
Liknelse 5
Entropi på flere nivå
I fysikken er det vanlig å lete etter sammenhenger i naturen for bedre å forstå naturen. Ovenfor har vi nevnt at energi kan forekomme i mer eller mindre "høyverdige" former, og at endringene normalt skjer "nedover". Teknologi kan imidlertid lage unntak i denne lovmessigheten. Her vil vi filosofere litt videre utfra dette prinsippet og se om energiprinsipper også gjelder for andre områder i livet.
Om vi her konsentrere oss om teknologi, så synes også denne å gå mot lavere kvalitet med tiden. Verktøy, motorer, transportmidler ol. blir slitt med tiden. Også her kan vi si at entropi eller uorden øker. All teknologien som vi mennesker har laget har begrenset levetid på grunn av slitasje og andre former for materialforringelse.
Nå vil kanskje noen nevne at det produseres bedre biler nå enn omkring århundreskiftet. Dette har imidlertid sammenheng med at mennesker har funnet bedre løsninger og metoder. Det er altså ikke innebygget i naturen at teknologi blir bedre med årene. Det er menneskelig tankevirksomhet og intelligens som gjør at ny teknologi er bedre enn den vi hadde tidligere.
Noen vil kanskje hevde at livet har utviklet seg fra ei "urcelle" og at dette er et eksempel på at naturen kan utvikle tekniske løsninger. Evolusjonsteorien er ikke bevist! Problemet her er at alle forsøk som er gjort etter at vitenskapen oppstod, tilsier at entropiloven gjelder innenfor alle naturfagets områder,
også i denne sammenhengen. Når noe overlates til seg selv vil vi få en negativ utvikling. Dette gjelder både menneskeskapte tekniske innretninger og biologisk liv. Slitasje, mutasjoner og andre forandringer som oppstår spontant, synes i sum å være negative. Det at en bil må "kjøres inn" og at de mørke bjørkemålerne syntes å ha et fortrinn på mørke bjørkestammer, er ikke et brudd på den generelle lovmessigheten som er nevnt ovenfor. Å si at livet har utviklet seg uten hjelp "utenfra" synes altså å "kollidere" med naturvitenskapelig erfaring. Biler
og annen menneskeskapt teknologi har da i hvert fall ikke utviklet seg til
noe bedre uten at mennesker har vært aktiv i utviklingen. Siden vi ikke kan
reise bakover i tid kan vi ikke bevise eller motbevise evolusjonsteorien. Her
vil vi likevel konkludere med at det er mer i pakt med entropiloven å si at det første livet er skapt av en intelligent skaper enn å si at det er en livløs natur som selv har "skapt" livet.

En interessant observasjon i det som er nevnt ovenfor, er at teknologi kan få energi til å "flyte mot strømmen". Videre nevnte vi at menneskelig tanke eller intelligens kan forbedre teknologi. Dette innbyr til å dele virkeligheten inn i tre nivå: energinivået, teknologinivået og tankenivået. Prinsippet for de to laveste nivåene er da at "alt går mot uorden". Det er imidlertid mulig for et overordnet nivå og gripe inn og "snu strømmen". Et naturlig spørsmål er da hva slags lovmessigheter som gjelder på tankenivået. Her er vi i ferd med å fjerne oss fra fysikken, men det skader vel ikke å vurdere om lovmessigheter fra fysikken også gjelder på andre områder. Om vi definerer tankenivået litt bredere og tar med hele samfunnets kulturarv, både kunnskap og moral, er det vel noen som vil hevde at ting var bedre før. Noen vil kanskje hevde at det er bedre nå. Historien har imidlertid vist at alle store kulturer har opplevd et forfall og har gått i oppløsning. La oss her et øyeblikk anta at det også på tankenivået finnes en lov som sier at "alt går mot uorden". Da er det naturlig å spørre om det finnes et annet høyereliggende nivå som eventuelt
kan snu en negativ utvikling i tankenivået. Her er det mange som vil svare ja. Dette nivået kan vi kalle det åndelige nivået. I fedrelandsalmen synger vi:
Vil Gud ikkje vera bygningsmann, Me fåfengt på huset byggja.
Vil Gud ikke verja by og land, Kan vaktmann oss ikkje trygja.
Så vakta oss, Gud så me kan bu I heimen med fred og hyggja.
Kanskje ligger det en sannhet her, som vår vestlige kultur først vil erfare om kristendommen ikke lenger får bli en sentral del av kulturarven. Her er det mulig å være uenig. Men
generelt er det vel lurt å være åpen for at vi kan lære noe i naturen som kan være nyttig på andre områder. Figuren til venstre viser det aktuelle "verdensbilde" med fire nivå. Uavhengig av om vi liker dette verdensbildet eller ikke, så kan den vel være med å gi oss en litt dypere forståelse visse sider ved vårt forhold til naturen.
Termofysikkens tredje hovedsetning
Som de fleste andre fysiske størrelsene vi omgir oss med har også temperatur
verdier som kan varierer mellom 0 og uendelig. Lengder, tidsrom
og krefter er eksempler på fysiske størrelser som kan ha en verdi fra
0 og oppover. I disse sammenhengene er det meningsløst å snakke om negative verdier.
Når vi likevel opererer med negative størrelser av og til, så har det sammenheng
med at vi har definert ei positiv retning. En lengde på f.eks. -1m (minus
en meter) vil
kunne bety at man går 1 meter tilbake eller noe tilsvarende, men selve lengden
er fortsatt 1m. Det er altså ikke noe forskjell på lengden
til 1m og -1m. Når det derimot gjelder 1°C og -1°C,
så er det to ulike verdier. Dette har da sammenheng med at vi har valgt å bruke
Celsius-skalaen som har som utgangspunkt at den temperaturen hvor vann fryser
skal ha verdien 0° og den verdien hvor vann koker ved normalt trykk skal ha
verdien 100°. Siden det finnes temperaturer langt under 0°C får vi da negative
temperaturer og det har endel uheldige sider i vitenskapelig sammenheng.
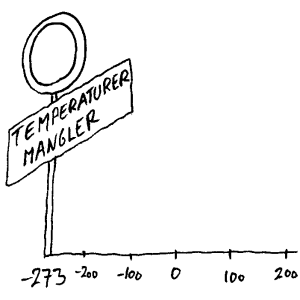
Det
er gjort ulike målinger for å finne ut hvor lave temperaturer det er mulig å
oppnå og man har da kommet fram til at den laveste temperaturen som er mulig
å oppnå er ca -273°C. Dette er en viktig verdi og en mulig kandidat til en tredje
hovedsetning i termofysikken er da:
Den laveste temperaturen man kan oppnå er
ca. -273°C. Denne temperaturen kalles det absolutte nullpunkt.
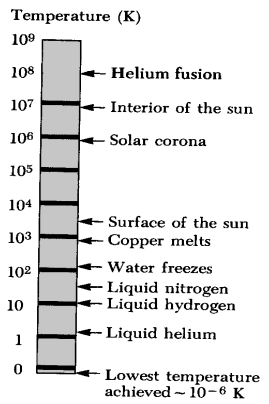
En
oversikt som viser ved hvilke temperaturer ulike fysiske prosesser
finner sted. Merk at skalaen er logaritmisk
Siden Celsius-skalaen er problematiske å arbeide med i vitenskapelige sammenhenger,
har man derfor valgt å innføre en ny skala til bruk i vitenskapelig sammenhenger.
Denne kalles Kelvin-skalaen og den har da definert 0-punktet ved det absolutte
nullpunkt, samtidig som den bruker Celsiusskalaen som utgangspunkt for å definere
hvor lang en grad er. Tilnærmet har vi da: 0°C=273K , 37°C=310K osv.
Om
vi går over fra Celsius-skalaen til Kelvin-skalaen så innebærer altså dette
at man plusser på ca. 273. Om vi derimot har en temperaturforskjell så vil denne
være den samme i både °C og K.
Årsaken til at det finnes en absolutt minimumstemperatur har da sammenheng
med at temperatur egentlig er et mål for indre bevegelser i ulike stoff. Når
så denne grensen er nådd betyr det at det som normalt beveger seg, da vil ligge
helt i ro. Det
er da generell enighet om at temperatur har å gjøre med indre bevegelser
i stoff, men det er da ikke enighet om det er molekyler, atomer eller elektroner
og protoner som beveger seg. Det skal vi komme tilbake til i forbindelse med
kinetisk gassteori.
Kinetisk gassteori (partikkelmodellen)
De fleste vet at vi bør lukke vinduene og skru på varmeovner om vinteren for å få
det varmt i husene våre. Hva er egentlig varme og hvordan sprer den seg? Hvis vakuum isolerer mer enn luft, hva er det da som gjør at vi mister så mye varme ut i universet som jo hovedsakelig består av vakuum? Hvorfor er det så kalt ute i universet når det er sol hele tiden? Slike og liknende spørsmål kan vi få i grunnskolen. Her er det nyttig å forstå hva vi mener med varme på et litt dypere plan. Det er ikke sikkert at vi skal lære elevene i grunnskolen alt dette, men det kan hjelpe oss som underviser å unngå feil svar eller "vet-ikke-svar".
Kinetisk gassteori - teoretisk beskrivelse av gassers fysiske egenskaper der de observerbare mikroskopiske egenskapene forklares som et resultat av de enkelte molekylers bevegelse. Kinetisk gassteori bygger på den klassiske fysikks bevegelseslikninger for enkelte molekyler, og summen av molekylenes virkninger finnes ved statistiske betraktninger.(Store Norske leksikon)
Gassteori - forkortet betegnelse på kinetisk gassteori som går ut på at molekylene i en gass beveger seg fritt om hverandre uten nevneverdig tiltrekningskrefter mellom seg. Molekylene har stor hastighet og deres gjennomsnittshastighet er et uttrykk for gassens temperatur. Deres støt mot karveggene betinger gassens trykk og deres støt mot hverandre betinger gassens utvidelse hvis den har anledning til å utvide seg... Den [teorien] viser god overensstemmelse med erfaringer og er av grunnleggende betydning for teorien om stråling og atomteoriens oppfatning av materien. (Store Norske leksikon)
En fysiker er vanligvis ikke fornøyd med å påvise ulike
sammenhenger. Han ønsker også å forstå hvorfor naturen
oppfører seg slik den gjør. Derfor prøvde man å finne
fram til en modell eller teori som kunne forklare de ulike fenomenene som er
beskrevet ovenfor. Resultatet ble kinetisk gassteori eller partikkelmodellen.
Her vil vi understreke at dette er en teori eller modell som ikke er bevist
selv om endel lærebøker synes å behandle den som et faktum.
I motsetning til vanlige lærebøker vil vi her se litt nærmere
på argumenter både for og mot den aktuelle modellen slik at leseren selv
kan vurdere hvor mye den skal vektlegges i egen undervisning.
1 Modellen kunne forklare tilstandsligningen
for idealgass (p·V/T=k)
Historien forteller at f.eks. Boyle antok at de kreftene som inngikk i lufttrykket
skyldes en eller annen form for frastøtende krefter mellom luftmolekylene.
Dette er et naturlige førstevalg når det gjelder å forklare
årsaken til gasstrykk. Om man f.eks. holder for åpningen til en engangsprøyte
og presser på stempelet vil vi kjenne en gradvis økning i mottrykket og det
er da naturlig å tenke at dette skylles frastøtingskrefter mellom molekylene.
Lærebøkene unnlater vanligvis å nevne dette og de starter
da direkte med å forklare lufttrykk
ved hjelp av kinetisk gassteori.

I pedagogikken er det et prinsipp som sier at læringsutbyttet øker om elevene
har forstått spørsmålet/problemstillingen før de får svaret. Det er med andre
ord lite virkningsfullt å presentere svar på spørsmål som elevene ikke har stilt
eller forstått. Her vil vi derfor bruke en mer problemorientert fremgangsmåte
enn det som er vanlig når man presenterer partikkelmodellen for gass. Her vil
vi da tenke på en engangsprøyte som da inneholder et visst antall luftpartikler/luftmolekyl.
På figuren til venstre har vi tegnet to av disse partiklene.
Boyle antok da at det var en form for fraskyvingskrefter mellom partiklene.
Siden vanlige lærerbøker sjeldent nevner denne mest nærliggende antakelsen,
så er det vanskelig å vite hvorfor man har forlatt den. Her følger en mulig
grunn. Forsøk viser at om vi måler trykket
i sylinderen samtidig som vi endrer volumet (før muspekeren over figuren), så vil
vi f.eks. erfare at luftrykket (p) dobles når volumet (V) halveres.
På partikkelnivå betyr det at en halvert avstand mellom to partikler (d) betyr
dobbelt kraft (F) som kan uttrykkes med følgende formel: F=k/d
hvor k er en konstant.
Andre fjernkrefter som f.eks. elektriske krefter følger formelen F=k/d²
og generelt kan vi si at en 1/d sammenheng er matematisk mer problematisk enn
en 1/d²-sammenheng. Her vil vi ikke gå videre inn på dette men bare nevne at
det er mulig å forklare de aktuelle kreftene som elektriske fraskyvingskrefter
mellom like ladninger om vi samtidig antar at det skjer visse endringer i selve
partiklene/molekylene. Rent matematisk er det imidlertid enklest å behandle
luftpartiklene som "stive partikler" som ikke lagrer noe energi internt,
men bare i form av eksterne bevegelser og eventuelt eksterne krefter. Siden
det da finnes en matematisk modell som kan forklare både trykkøkningen og temperaturøkningen
vi observerer i slike tilfeller (kinetisk gassteori) , så valgte man da
å anta at det ikke finnes noen frastøtingskrefter mellom luftpartiklene i slike
tilfeller.
Kinetisk gassteori Kjernen i denne modellen er at trykk og
temperatur er direkte knyttet opp mot bevegelser i de partiklene som utgjør
gassen. Her vil vi da understreke at det er snakk om bevegelser av selv gasspartiklene
som utgjør varmen og ikke bevegelser i eller omkring dem. Sannsynligvis har
man til alle tider tenkt seg at varme er en form for bevegelse siden varme f.eks.
kan bryte opp ulike bindinger på ulike nivå. Også de som argumenterte for Kalori-modellen
(navnet på en modell som ble brukt før kinetisk gassteori ble innført)
tenkte seg at varme var en form for bevegelse men denne foregikk da i hovedsak
mellom partiklene i det mediet man kalte eteren.
En tredje mulighet er at temperatur først og fremst er knyttet til bevegelser
i luftpartiklene. Hensikten med å nevne dette her er da bare å få fram
at det i utgangspunktet finnes ulike måter å forklare varme, og kinetiske
gassteori representere derfor en av flere.
Det var den sveitsiske matematikeren Daniel Bernoulli (1700-1782) som utviklet
det matematiske grunnlaget for denne modellen. Han viste f.eks. at trykket vil
dobles om volumet halveres (Boyles lov) om vi antar at trykket er forårsaket
av luftpartiklenes stadige støt mot omgivelsene. Videre viste han at om vi antar
at varme-energien i luft egentlig er den kinetiske energien til luftpartiklene
(Ek=½mv²), så vil man også få den kjente sammenhengen mellom temperatur
og trykk (Gay-Lussac's lov). Jo fortere luftpartiklene beveger seg, jo flere
og kraftigere støt blir det mot veggene og tilsynelatende hadde man kommet fram
til en enkel varmemodell som kunne forklare begge de viktigste lovmessighetene
som gjelder for luft og andre gasser. (Boyles lov og Gay-Lussac's lov))

En
måte å anskueliggjøre hvordan Bernoulli påviste at tilstandslikningen følger
av kinetisk gassteori, er å tenke seg en engangsprøyte med luftpartikler inni.
Gassen i denne sprøyta vil da bestå av mange partikler. I prinsippet er da trykk
og temperatur forårsaket av mange luftpartikler som hver bidrar like mye, og
derfor er det mulig å forenkle totalbildet og tenke seg en partikkel som spretter
fram og tilbake mellom stempelet og bunnen av sprøyta. Om vi så presser stempelet
inn slik at volumet blir halvert, så vil avstanden som partikkelen beveger seg
mellom støtene bli halvert og antall støt pr tidsenhet på veggene vil da bli
fordoblet. Dette illustrerer da hvordan sammenhengen mellom trykk og volum kan
forklares ved hjelp av kinetisk gassteori. Om vi i stedet varmer opp gassen
til dobbel temperatur (ifølge Kelvin-skalaen) forteller tilstandslikningen at
trykket vil bli doblet. Modellen forteller da at hastigheten til gasspartiklene
økes med √2 (roten av 2), som da medfører at antall støt
mot veggene også øker med √2. Trykkøkningen som da
er et resultat av at både farten til partiklene øker og antall partikkelstøt
pr tidsenhet øker, vil da øke med √2·√2=2
som da betyr en dobbling av trykket når temperaturen dobles.
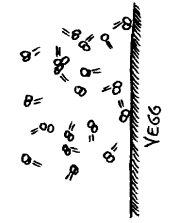
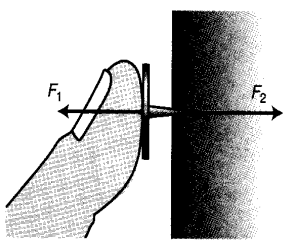
Lufttrykk
mot en vegg er ifølge kinetisk partikkelteori summen av støt
fra luftmolekyl
Utfra denne modellen kan vi forklare lufttrykk som et resultat av at mange luftmolekyl treffer ei flate og spretter tilbake. Hvert støt vil gi flata et lite puff (kraft), og til sammen vil de da representere en betydelig kraft på flata. Kraften på en negl (1cm²) som skyldes lufttrykket er da 10N som tilsvarer vekten av et lodd på 1kg. Trykket på 1dm² (et lite hode) vil da tilsvare 100kg. Denne
modellen forklarer da også temperatur i luft. Om vi definerer v som midlere hastighet (gjennomsnittshastighet) til molekylene i en gass og m som massen av et gassmolekyl, får vi følgende sammenheng:
T er da temperaturen oppgitt i Kelvin (absolutt temperatur). Konstanten har følgende tallverdi: a = 2,07 10-23. Hvis man vil beregne gjennomsnittsfarten til luftmolekylenen så kan
man bruke formelen som er nevnt ovenfor. Her bruker vi massen til et oksygenmolekyl og romtemperatur
(20°C)?
Gj.farten: v = (
2aT/m)½ = (
2*2,07-23J/K*293K / 5,4-26kg)½ = 480m/s
= 1700km/h
Lydhastigheten er til sammenlikning 340m/s.
Robert Brown 1827
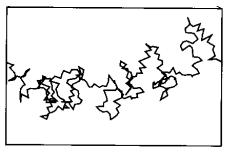
Man ser i mikroskopet
at partikler spretter tilfeldig i ulike retninger og over tid kan
man tenke seg at en bestemt partikkel får en slik bevegelse
som er tegnet her
2 Man trodde at modellen kunne forklare brownske bevegelser
En oppdagelse som styrket denne teorien ble
gjort av engelskmannen Robert
Brown i 1827. Bakgrunnen for kinetisk gassteori var at man prøvde å forklare
gasslovene som man hadde oppdaget. På 1800 tallet var de fleste gasslovene
oppdaget og disse trengte da en forklaring. Man hadde utviklet kinetisk gassteori og
i denne sammenhengen var det vel de såkalte Brownske bevegelsene som fremstod som det viktigste argumentet for at denne teorien
måtte være rett. Brown's
oppdagelse i 1827 bestod i at han så at blomsterstøv/pollen oppløst i vann hadde uregelmessige bevegelser. Partiklene lå altså ikke i ro, men var i stadig bevegelse nede i vannet. Hans
første forslag var at han observerte levende organismer, men senere ble
det klart at det var livløse partikler han observerte. Disse bevegelsene krevde da
en forklaring. Konklusjonen ble at bevegelsene var et resultat av at væskemolekylene, som er for små til å bli sett i et mikroskop, beveget seg kontinuerlig. Det var så disse molekylene som man
antok støtte mot pollenpartiklene og gav disse de aktuelle bevegelsene. Noe tilsvarende kan vi også
se i støvpartikler eller røykpartikler i luft. Forklaringen
ble da at de små luftmolekylene (vannmolekylene) var utsatt for store
kinetiske bevegelser og det var da støt fra disse som gjorde at de mye
større støvpartiklene fikk sine karakteristiske sikksakkbevegelser. Temperaturbegrepet hadde lenge vært et mysterium og da det viste seg
at man kunne forklare gasstemperatur som den kinetiske energien til
gasspartiklene, så fikk kinetisk gassteori mange tilhengere. Man antok
da at det var følgende sammenheng mellom det vi kan kalle gjennomsnittshastigheten
til gasspartiklene og temperaturen:
Denne forteller f.eks. at om vi dobler gjennomsnittshastigheten til gassmolekyler
så vil temperaturen firedobbles. Konklusjonen ble derfor at molekyl og atom i
en gass er i stadige bevegelser. Intensiteten på disse bevegelsene bestemmer så temperaturen til gassen. Temperatur er altså en form for kinetisk energi i atom og molekyl. Temperaturen overføres mellom molekylene omtrent som klinkekuler overfører kinetisk
energi til hverandre ved sammenstøt.
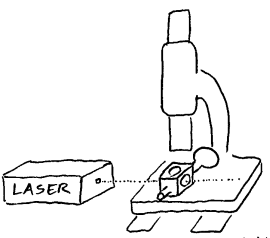
Utstyr
for observasjon av brownske bevegelser
Demonstrasjon
av Brownske bevegelser
Ved hjelp av et enkelt eksperiment er det mulig
å demonstrere brownske bevegelse i luft. For å være sikker på at vi skal se bevegelsene er det en fordel med en laser og et spesiallaget røykkammer med bunn og vegger av metall. Om ikke skolen har dette utstyret, kan en lyskaster og ei spalte samt ei glass-skål med glassplate til lokk gjøre nytte. Røyken kan lages av myggspiral, sigarett eller liknende. I røykkammeret suges da røyken inn. Om vi bruker glasskål, kan vi plassere røykkilden i selve skåla. I alle tilfeller må vi ha et godt
mikroskop som forstørrer omkring 50-100 ganger. Om vi bruker glasskål kan vi legge ei metallplate i bunnen av denne for å stabilisere luftstrømmer som kan oppstå. La så
lysstrålen komme horisontalt inn fra siden. Om luftstrømmene er for sterke, slik at støvpartiklene ser ut som "snøstorm", kan det hjelpe å flytte skåla slik at vi observerer nær kanten av skåla. Merk at vi ser de relativt store røykpartiklene. Man
antar da at bevegelsene til disse partiklene skyldes svært raske bevegelser
til de langt mindre luftmolekylene.

På
internett kan man finne diverse Java-applets som illustrerer Brownske bevegelser.
Et eksempel: http://www.phy.ntnu.edu.tw/java/gas2D/gas2D.html
Gif-animasjonen til venstre som er lånt fra nettsida http://physics.nad.ru/Physics/English/thermo.htm,
viser da det samme prinsippet. Den blå kula epresenterer en røkpartikkel, mens
de røde kulene representerr gassmolekylene. Av en eller annen grunn er det mye stoff om kinetisk gassteori på
internett og i lærebøker. Samtidig er det vanskelig å finne informasjon om de
problemene som er knyttet opp mot den aktuelle modellen.
Så lenge det i L97 relativt tydelig sier at man skal bruke denne modellen
i grunnskolen (lenke) og
siden det er et faktum at partikkelmodellen er en av flere modeller som
kan forklare f.eks. temperatur, så er det viktig å presentere denne
modellen her. Men det er samtidig et vitenskapelig ideal at man ikke underslår vitenskapelige
argumenter som taler mot de modellene som presenteres i ulike sammenhenger.
Derfor vil vi her kort nevne et argument som setter et stort spørsmålstegn med
om Brownske bevegelser i et hele tatt er et argument for kinetisk gassteori:
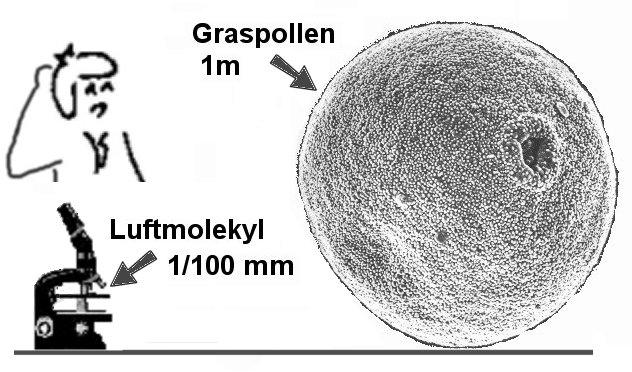
Figuren
til høyre illustrerer det virkelige størrelsforholdet mellom gassmolekyl/vannmolekyl
og røkpartikler/pollenkorn som vanligvis brukes for å vise Brownske bevegelser.
I litteratur kan vi finne at pollenkorn som er i størrelsorden 10-100 mm
(10-5-10-4m) og gassmolekylene på den andre siden vil
ha en størrelsorden omkring 10-10m og har en innbyrdes avstand omkring 10-9
m, mens vannmolekylene har en innbyrdes avstand omkring 10-10m. Om vi tenker oss en skalamodell hvor et gresspollen har en diameter på 1
m. så betyr det at gasspartiklene vil få en størrelse på 1/100 mm (10-5
m) og vi må derfor bruke mikroskop for å se dem. Ifølge vanlige lærebøker tenker
man seg så at slike små partikler som kolliderer med det store gresspollen
(eller røkpartikler) vil forårsake "spretting" fram og tilbake
slik vi observerer i virkeligheten! Sannsynligvis vil ikke cm-store klinkekuler
kunne forårsake at denne store pollenmodellen vil sprette fram og tilbake og
da er det enda mer mindre sannsynlig at partikler som er 1000 ganger mindre
vil gjøre det. Merk at dette virkelige størrelsesforholdet er et helt
annet størrelseforhold enn de vi ser i f.eks. gif-animasjonen ovenfor, og hadde
folk vært klar over hva slags størrelseforhold det egentlig er snakk om, så
er det mye som tyder på at man ville slutte å bruke Brownske bevegelser som
argument for kinetisk gassteori.
Problem med temperaturforståelsen som følger av kinetisk
gassteori
Temperatur er noe som finnes i både fast stoff, væske og gass og derfor skulle
man forvente at det var mulig å forklare temperatur på en ensartet måte i alle
disse tre sammenhengene. Om vi f.eks. skal forklare hva elektrisk strøm er,
så er det uproblematisk å si at det er forflytning av elektroner i en retning.
Dette er da en forklaring som fungerer for både fast stoff, væske og gass siden
alle inneholder atomer som igjen inneholder elektroner.
Så enkelt er det imidlertid ikke om vi skal forklare temperatur og tar
utgangspunkt i temperaturforklaringen som følger av kinetisk gassteori. Den
aktuelle temperaturforklaringen forutsetter da at gass består av partikler (molekyl/atomer)
som kan bevege seg fritt i forhold til hverandre og følgelig kan de ha en fart
(v) og en kinetisk energi (½mv²). Temperatur er da knyttet opp mot denne
energien. Tidsmessig vil da kontakten mellom partiklene i de såkalte elastiske kollisjonene
være liten i forhold til den tiden partiklene beveger seg fritt og det er da
de frie bevegelsene som definerer temperaturen. Temperaturen er ifølge kinetisk
gassteori proporsjonal med v² hvor v er gjennomsnittsfarten for
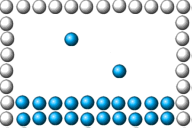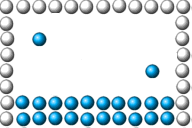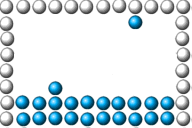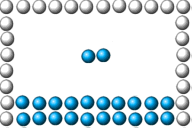
de ulike partiklene. Animasjonen til høyre viser to gassmolekyl (vanndamp)
som befinner seg i luftrommet under et glass som er satt på hode ned i vann.
Gassmolekylene vil da ifølge kinetisk gassteori har en fart i størrelsorden
500m/s og kollidere både med andre gassmolekyl i tillegg til at de kolliderer
med vannflata (væske) og glassveggene (fast stoff). Temperaturen i den aktuelle
gassen er da bestemt av farten til molekylene i gassen. Så langt er det mulig
å danne seg et fysisk bilde av hva denne modellen sier. Problemet oppstår når
man også vil danne seg et fysisk bilde av temperatur i væsker og faste stoff.
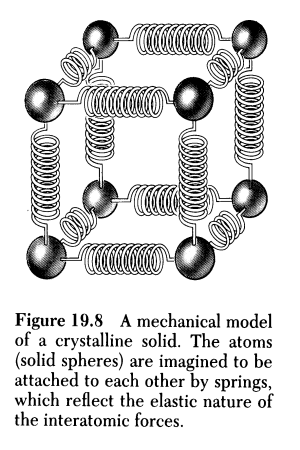
I motsetning til i gasser, så er vel
alle enige om at det i væsker og fast stoff finnes indre krefter som holder
disse sammen. Det betyr at eventuelle
bevegelser i de partiklene som utgjør væsker og faste stoff ikke vil være frie
slik som i gassmodellen ovenfor. Nå er det vanskelig å finne lærebøker som behandler
temperatur i gass og væsker på en tilfredstillende måte. Noe ganger nevner man
kort at det er snakk om partikkelvibrasjoner uten at man nevner noen tallverdier
for f.eks. fart som da er nøkkelen i temperaturforklaringen som gjelder
i gasser. Figuren til høyre er hentet fra Serway: Physics for Scientists and Engineers
(1990) p 513. og denne viser da at kreftene mellom partiklene i faste stoff
kan sammenliknes med fjærer. Disse fjærene vil da holde partiklene på plass
samtidig som partiklene kan vibrere litt fram og tilbake.
Her er det ikke noe poeng i å forklare de problemene som kinetisk partikkelmodell
har i sammenheng med temperatur i væsker og fast stoff, men vi vil bare kort
nevne at problemene er tosidig. På den ene siden har man hatt problemer med
å lage en kvantitativ korrekt mekanistisk modell som kan lager så
mye varmeenergi som det egentlig er snakk om. På den andre siden har man problemer
med å forklare fysisk hva som egentlig skjer når varme lagres i temperaturendringer
og faseoverganger mellom fast stoff, væske og gass.
Poenget her er da heller å trøste dem som har prøvd å forstå kinetisk partikkelmodell,
men har erfart at de har mislykkes. Det kan nemlig være at det ikke er egne
evner som er problemet, men selve den kinetiske partikkelmodellen.
Ifølge en elektromagnetisk forklaringsmodell er temperatur et mål for frekvenssammensetningen
i varmestrålingen som omgir oss. Det er da ladningene (primært elektronene)
i molekylene som vibrerer og lager strålingen mens molekylene og atomene
har bare mindre bevegelser.
En alternativ temperaturmodell
Det
er et faktum at alle gjenstander som har temperatur over det absolutte nullpunkt (-273°
C) vil sende ut elektromagnetisk stråling . og det kan da forklares ved å si at ladninger/elektroner vibrerer og forårsaker denne. Når temperaturen er -273°
C (= 0 Kelvin) ligger da elektronene helt i ro. Ved normale temperaturer sier vi at stoffene sender ut varmestråling. Om temperaturen blir i
størrelseorden tusen °C vil gjenstandene også sende ut lys (de gløder). Hvis vi da rett og slett sier at temperatur er et uttrykk for hvor voldsomme elektronene vibrerer så får vi en modell som kan forklare alt det vi observerer omkring oss til daglig. Det er f.eks. elektroner som er hovedelementet i kjemiske bindinger og om elektronbevegelsene øker vil kjemiske bindinger svekkes (ved koking av mat ol.). Tilsvarende kan vi forklare varmeutvidelse og faseoverganger om vi antar at elektronene i hovedsak befinner seg ytterst i atomene/molekylene. Jo mer disse elektronene vibrerer, jo mer plass trenger de og vi får da utvidelse. Om vibrasjonene blir for store vil de ulike bindingskreftene mellom atomene/molekylene i fast stoff/væske svekkes og vi kan da få overgang til væske/gass. Nå ulike gasser og luktstoff sprer seg relativt fort i luft, så er det klart at molekylene i luft beveger seg som helhet. Men her vil vi da understreke at det er mulig å tenke seg at hoveddelen av energien i de såkalte termiske bevegelsene er knyttet til interne elektronvibrasjoner i luftmolekylene, og at det bare er en liten del av den totale energien som da er knyttet til bevegelsen av selve molekylene.
Nå vil vi ikke bruke tid på denne alternative modeller som mange mener
kan forklare temperatur på en mer forståelig måte, men vi vil bare kort nevne
hva som hovedsakelig skiller partikkelmodell fra em-modellens forklaring av temperatur.
Mens partikkelmodellen hevder at varmeenergien ligger i bevegelser til hele
partiklene (atomer/molekyl) så sier em-modellen at varmeenergien er knyttet
opp mot bevegelser av elektroner som er en mindre del av de aktuelle
partiklene som bed et fellesnavn kalles ladninger. Det vil f.eks. si at grunnen til at ting utvider seg når de blir
oppvarmet er at selve atomene/molekylene blir større fordi interne deler (elektroner)
beveger seg (vibrerer) mer (lenke). Ifølge tradisjonell partikkelmodell så forklares denne utvidelsen
som en følge av at hele atomene/molekylene beveger seg mer når temperaturen
øker.
Et temperaturforklaringseksempel: Feber betyr at temperaturen i kroppen
øker og høy feber kan da være farlig fordi høye temperaturer vil
kunne ødelegge proteinstrukturen i cellene våre. Det er f.eks. en slik endring
av proteinstruktur som skjer når vi koker egg og poteter. Resultatet blir da
at proteinene får en annen form som kanskje er lettere å fordøye, men de vil
da ikke lenger fungerer i forhold til sin opprinnelige hensikt. Hvordan skal
vi så forestille oss hva som skjer når temperaturen øker i organisk vev? Skal
vi tenke oss at atomene i kroppen vår normalt vil vibrere og bevege seg med
hastigheter på nivå med lydhastigheten men likevel bevare strukturen slik som
den vanlige modellen sier? Når vi så får feber vil de vibrere enda litt
mer og noen viktige atom i proteinene våre vil da kunne rive seg løs slik at
proteiner blir ødelagt. Alternativet er da å tenke at det er elektronene i
de ulike kjemiske bindingene som vil vibrere mer. Når så temperaturen
når en viss verdi vil disse bindingene kunne brytes fordi elektroner hopper
fra ett sted til et annet og forårsaker nye og kanskje uønskede bindinger.

Eksempler
fra en lærebok: I undervisningssammenheng ønsker vi vanligvis å
presentere definisjoner og lovmessigheter som er mest mulig generelle. De
som lager lærebøker har derfor av og til prøvd seg
på å anvende partikkelmodellens temperaturbegrep i f.eks. væske
og fast stoff. Se eksempel fra Univ.91 Nat7-9 Infobok s31. Problemet er imidlertid at slike forklaringer ofte
vil
forvirre de som tenker og de som virkelig har forstått partikkelmodellen
vil da vanligvis unngå å bruke partikkelmodellen i slike sammenhenger.
I
figuren til høyre har vi et eksempel på at man i en lærebok har oppgitt en verdi
for hvor fort vannmolekyler beveger seg (600m/s). Ting tyder på at verdien er
for høy, men selv om den skulle være rett ifølge teorien, er det vel ikke så mange som opplever
at denne henvisningen til partikkelmodellen er oppklarende i forhold til å forstå
de ulike fysiske egenskaper ved vann.
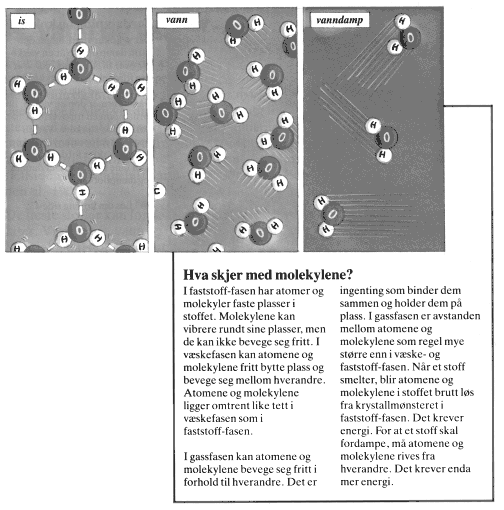
I figuren over har man prøvd
å illustrere/tegne partikkelbevegelsene ved hjelp av "fartsstreker". (Univ. 91
Nat7-9 Inforbok s42) Selv om hastigheten i partikkelbevegelsene i fast stoff og væske må
være endel mindre enn hastigheten i gass fordi det avgies endel energi
ved faseovergangene fra gass til væske og fra væske til fast stoff,
så vil mange oppleve det vanskelig for tanken å kombinere slike relativt kraftige
bevegelsene med de relativt stabile strukturene som tross alt finnes i væsker
og fast stoff.
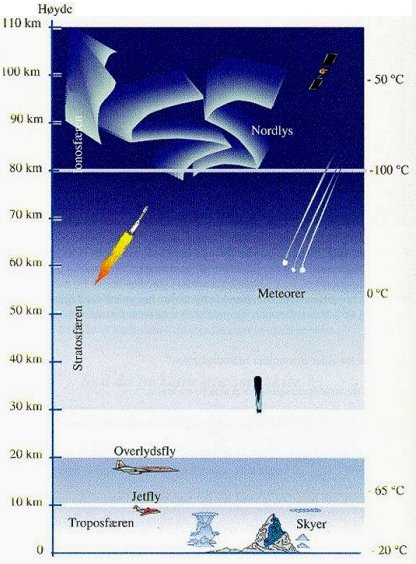
Figur fra NKS97 Forsøk og fakta 8 s192
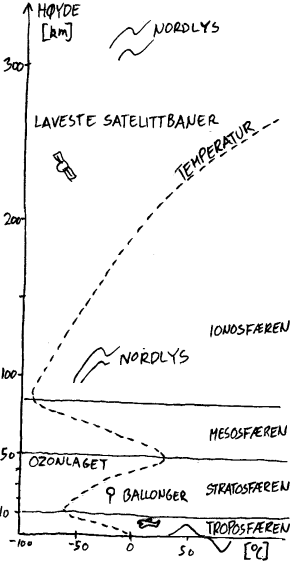
Temperaturkurven
viser antatt molekylfart ifølge partikkelmodellen, og ikke
den temperaturen vi ville målt med et vanlig termometer
Tvetydige temperaturverdier på grunn av kinetisk gassteori
Etter at L97 kom ble det laget nye lærebøker i Norge og jeg husker at jeg
fikk henvendelser fra lærere i grunnskolen i forbindelse med en figur
i en av de nye lærebøkene. En slik figur er vist til høyre(NKS97 Forsøk og fakta 8 s192.):
En lærer fortalt da at en elev mente at det måtte være noe feil med figuren
og læreren selv klarte da ikke å "forsvare" figuren. Det var da temperaturverdiene
som er markert til høyre på figuren som eleven satte spørsmålstegn ved.
Hva er så problemet? All erfaring viser at når vi beveger oss oppover
i atmosfæren vil temperaturen synke. Om vi med et termometer og
måler temperaturen ved havnivå og på en høy fjelltopp vil vi normalt måle lavere temperatur i høyden. Så
langt er det ikke noe uenighet, selv om det kanskje ikke er like enkelt å forklare
hvorfor det er slik. Skulle det ikke bli varmere jo nærmere vi kommer
sola? Her vil vi ikke forfølge denne tanken, men bare nevne at problemet man
har med å forklare hvorfor det er kaldere oppover i atmosfæren sannsynligvis
har
sammenheng med at man tror at kinetisk gassteori er rett.
Hovedproblemet for eleven og læreren i dette tilfelle var da temperaturforholdene
videre oppover i atmosfæren. På figuren ser vi at det er en temperaturstigning
mellom ca 13km og 50km og over ca 80km. Vil virkelig temperaturen stig når man
beveger seg utover i atmosfæren? Og hvordan er det i tilfelle mulig å forklare
denne temperaturstigningen? Dataene til skissen under til høyre er hentet fra
andre kilder og denne viser da at temperaturen utover i universet er høyere
enn nede ved jordoverflaten! Hva skal man da tro? Er det ikke sant at det er kaldt i universet slik man kan lese i andre sammenhenger?
Noe kan da ikke være varmt og kalt samtidig?
Her vil vi først slå
fast at det er kaldt i universet. Om vi tar med oss et vanlig termometer
i et romskip og holder det ut av vinduet på ulike steder så er det
et faktum at vi vil registrere en jevn synkende temperatur opp gjennom
atmosfæren. Når romfarerne er ute i universet
så har de svært tykke romdrakter på seg og en hovedårsak til dette er da nettopp
at de ikke skal fryse. Men hvorfor forteller så lærebøker i grunnskolen at temperaturen
øker utover i atmosfæren?
To typer temperaturmålinger
Her vil vi understreke at det finnes to prinsipielt
ulike metoder å måle temperatur på. En av disse er da å
bruke vanlig termometer med kvikksølv, rødsprit, elektroniske termometer eller
hånda. Disse metodene vil da alle fortelle at det er svært kalt ute
i universet. Men den aktuelle kurven til venstre er ikke basert på slike termometer.
Innenfor atmosfæreforskning er det vanlig å beregne temperaturen utfra
målinger av det elektromagnetiske spekteret fra ulike deler av
atmosfæren. Man bruker så
diverse antakelser som er basert på kinetisk gassteori og kvantemekanikken
for å omdanne spektraldata til de aktuelle temperaturene. Ifølge vanlig logikk,
så er det vanlig å tenke at det må være noe feil når
ulike målinger
gir ulike temperatur i samme område. Men slik tenker man tilsynelatende
ikke blant dem som studerer temperatur i atmosfæren. Når
man får ulike temperaturer med ulike målemetoder sier man da bare at det
er snakk om ulike typer temperaturer.
Merk ellers at nyere legetermometer som måler temperaturen i øret
også er basert på måling av strålingsspekter, men i
dette tilfellet har man kalibrert termometerne ved hjelp av den gamle typen
termometer som man egentlig stoler mest på. Det betyr videre at man
får samme temperatur med begge typene termometer. Grunnen til at man i
praksis har gått over til å bruke spektraltermometer er da
at de gir raskere resultat på en enklere måte. De måler
da den varmestrålingen som kommer fra det indre av øret og de gir da rett temperaturverdier
fordi det er en sammenheng
mellom frekvenser i utstrålingen fra øret og temperaturen i kroppen.
Nå forteller vanlige lærebøker svært lite om hvordan man konkret har gått
fram for å finne den aktuelle temperaturkurva som er vist i figurene her, men
det faktum at man med bruk av "spektraltermometer" får helt andre
verdier enn man ville fått om man brukte vanlige termometer. Hadde f.eks. moderne legetermometrene gitt
så forskjellige verdier fra de man får med vanlige termometre, hadde man helt
sikkert ikke tatt dem i bruk. Men når det gjelder moderne målinger av temperaturen
i ulike lag i atmosfæren, så bruker man altså en type instrument som gir
andre verdier enn de verdiene man ville fått med standardinstrument. Noen mener
at dette er en klar antydning om feil i kinetisk gassteori og kvanteteorien og at vi bør utvikle
andre modeller for omregning fra spektraldata til temperaturer i atmosfæren.
Om man spør de som driver med forskning innenfor dette område om hva de mener
om det som er nevnt her, så vil de sannsynligvis innrømme at den aktuelle temperaturkurven
som er vist på figuren handler om noe annet enn det vi til vanlig kaller temperatur.
Men de vil da sannsynligvis også mene at de temperaturverdiene som de
bruker er mer interesanne enn den klassiske temperaturverdien
som er basert på bruk av vanlige termometer. Problemet her er da om man i skoleverket
og i samfunnet generelt er tjent med å operere med 2 ulike temperaturbegrep.
Alle lærere vil sannsynligvis være enige om at det er pedagogisk uheldig å knytte
to ulike og motstridende definisjoner til ett og samme begrep og her vil vi da bare konkludere
med at en lærer som skal undervise om temperatur bør være klar over hvilke konflikter
som er innebygd i det aktuelle lærestoffet. Hvis læreren underviser om temperatur
på en dogmatisk måte så er det stor sannsynlighet for at noen elever som tenker
litt dypere enn andre, vil bli forvirret og det er vel ikke det skolen ønsker.
Nå er det imidlertid et faktum at man i norske lærebøker finner det
vi kan kalle moderne temperaturer som da ikke stemmer med det
vi kan klassiske temperaturer og som en slags "førstehjelp" er det mulig å si at de aktuelle atmosfærekurvene
handler om antatte gjennomsnittshastigheter til gassmolekyl. Vi kan derfor
tenke på disse verdiene som et uttrykk for hvor raskt man tror partiklene beveger
seg ulike steder i atmosfæren. Klassisk temperatur er på
den andre siden har sammenheng med energitransport mellom ulike steder.
Steder som avgir mer energi til omgivelsene en de mottar fra omgivelsene
har da høyere temperatur enn omgivelsene. Det er videre slik
at lysstråler fra for eksempel sola vil forstyrre temperaturmålinger
og derfor er det en regel at temperaturmålinger skal foregå
i skyggen. Temperatur er altså knyttet opp mot det vi kaller varmestråling
som da har lavere frekvens enn lysstråling.
Begrepet varme
På samme måten som de offisielle temperaturdefinisjonene skaper
problemer, så kan vi vel også si at de offisielle varme-definisjonene
skaper problemer. Her vil vi da bare kort nevne at man i termofysikken, som
er den delen av vitenskapen som i hovedsak handler om varme, har valgt
å si at varmebegrepet skal knyttes opp mot energi som beveger seg fra ett
område til et annet. Dette representerer da en innsnevnring i forhold
til det man i dagligtale kaller varme. I dagligtale vil man f.eks si at
det er varme i en ovn, men i termofysikken kaller man da denne energien
i ovnen for indre energi og varmebegrepet knyttes da bare til den energien som
forlater ovnen. En slik innsnevring av varmebegrepet vil sannsynligvis
skape forvirring i grunnskolen og det er da grunnen til at vi har foreslått
å bruke en videre definisjon her.
Miljøperspektivet har fått økt betydning de senere årene fordi mange av de
problemer vi opplever har sammenheng med det vi kan kalle forurensning. En kort
definisjon av forurensning er: stoff på feil sted. I denne sammenhengen
er det snakk om å finne fram til metoder for å omplassere stoff .
Det er
da snakk om både fysiske, kjemiske og biologiske prinsipp. Her vil vi da gi
en innføring i noen fysiske prinsipp som vi må ta hensyn til i forbindelse med hvordan stoff reagerer i forhold til hverandre
når de kommer sammen. Dette er et stort og ofte uoversiktlig tema som inkluderer
fagstoff fra de fleste fagområdene og målet her er da å gi en kort og generell
innføring i noen få prinsipp, ikke en utfyllende beskrivelse av
dagens metoder for å løse forurensningsproblemene. Det er viktig at en lærer har kunnskap om dette
om han skal kunne svare på de ulike spørsmålene
som ofte dukker opp i forbindelse med aktivitetsbasert undervisning.
Her
følger først en innføring i noen sentrale begrep:
Diffusjon
Når vi merker lukt, er det "luktmolekylene" som sprer seg utover mellom gassmolekylene i lufta. Slik spredning av molekyler i gasser,
væsker (og fast stoff) kaller vi diffusjon. (Univ.91 Nat7-9 Infobok s30)
Et demonstrasjonseksempel som viser diffusjon får man om man f.eks. skreller
en appelsin i et klasserom og ber elevene gi beskjed etterhvert som de merker
lukten. Diffusjon skjer også i vann og om man slipper litt farge i vann vil
man kunne se hvordan ulike fargestoffene sprer seg i vann. Figuren til høyre
er ellers et eksempel som viser at vannmolekyl også kan diffunderer gjennom/langs
med et lommetørkle. De vil da difundere lettere enn andre større partikler og følgelig har man her
en mekanisme som kan brukes
for å fjerne visse stoff fra vann.
Osmose Osmose oppstår når to væskemengder med forskjellig konsentrasjon av oppløste stoffer befinner seg på hver sin side av ei halvgjennomtrengelig hinne. Eks: økt trykk i øyet når vi bader i ferskvann (Univ.91 Nat7-9 Infobok s32)
I figuren til høyre er det festet en halvgjennomtrengelig membran
til trakten inni begerglasset. Om man f.eks. har litt salt inni trakten vil
vi kunne oppleve at vann trenger gjennom membranen fra ferskvann til saltvann
og forårsaker at trykket øker inni trakten. Et eksempel på en halvgjennomtrengelig
membran er den hinnen man finner på innsiden av et egg. Slike hinner er de lett
og få tak i og de kan da brukes i forsøk med osmose.
Adhesjon
Adhesjon er krefter som gjør at forskjellige stoffer trekkes mot hverandre. Tiltrekningen som skjer mellom glass og vann, blir kalt adhesjon. Den kommer av elektriske krefter mellom molekylene. Eks: tiltrekkes glass, frastøter stearin, hårrørskrefter. (Univ.91 Nat7-9 Infobok s36)
Figuren til høyre viser at det oppstår tiltrekningskrefter
mellom glass og vann og følgelig vil glasset dra vann litt oppover, mest
i de tynne rørene. Hvordan kan vi forklare dette? (sammenheng mellom
areal og volum/vekt) Stearinlyset
på sin siden vil avvise vannet og følgelig heller vannflaten nedover
nær stearinlyset.
Overflatehinne
I bøker beregnet på mindre barn er det vanlig å
ha med litt om den såkalte overflatehinna til vann. Det er mulig med
enkle midler å få til morsomme forsøk og det er nok hovedårsaken
til at dette er med. På den andre siden er det relativt vanskelig å
forklare hva som skjer og når selv ikke lærebokforfattere synes
å forstå dette begrepet er det vel tvilsomt om man bør bruke
mye tid på det i barnetrinnet. Forsøkene vil
nok engasjere barna, men det gjør ved de fleste aktivitetene i denne
alderen. Problemet er at forsøk som elevene ikke skjønner kan utvikle en slags
frustrasjon som gjør at de senere vil unngå det de følge
litt ubehag ved fordi de ikke skjønte hva de gjorde.
I boka Fysikkaktiviteter i barnehage og småskole finner vi blant
annet: "Den faglige forklaringen er den samme i alle tilfeller: På
grenseflaten mellom luft og vann har vannet andre egenskaper enn vannet dypere
nedi. Som navnet sier er det faktisk en hinne på vannet som er forbausende
sterk. Denne hinna kan vi ødelegge, ikke ved hjelp av noe spisst eller
et hardt slag, men med kjemiske midler. Det beste kjemiske midlet er nettopp
såpe" (s 100). Her vil vi ikke bruke mye tid på dette sitatet,
men bare si at det i det minste er sterkt misvisende. Det er nemlig ikke snakk
om en hinne slik vi vanligvis forstår ordet, som noe som skiller seg fra
det som ligger under. En bedre måte å forklare fysikken bak det
litt misvisende begrepet overflatehinne er å henvise til sterke interne
elektriske krefter mellom vannmolekylene fordi vannmolekylene er relativt sterke dipoler.
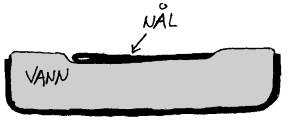
Vannmolekylene
trekker så sterkt på hverandre at nålen ikke klarer
å trenge ned mellom vannmolekylene. Av samme grunn kan skåla
overfylles med vann uten at det renner over.
Hva
er overflatehinne: Mange har sett insekter som kan gå på vannet og at
små metallgjenstander (nåler, barberblad o.l.) kan flyte på vann. Noen forklarer det ved å henvise til en overflatehinne. Her vil kortsi
at dette er et uheldig ord som gir uheldige assosiasjoner. Årsaken til dette fenomenet er egentlig
at vannmolekylene blir sterkere tiltrukket av hverandre enn av f.eks. jern. Når vi så legger ei nål forsiktig ned på ei vannflate kan vi tenke at vannmolekylene fungerer som en menneskemasse som holder hverandre i hendene. Det er da vanskelig for andre å trenge inn i en slik menneskemasse. Men om vi f.eks. har såpe i vannet betyr det at vi tilfører molekyl som er svakere dipoler og disse vil da gå inn mellom vannmolekylene og svekke båndene mellom disse slik at nåla kan trenge inn mellom vannmolekylene
og synke. Forklaringen på overflatehinnen er altså ikke at vannet omgir seg med en spesiell hinne, men at
det i rent vann er sterke bindinger mellom vannmolekylene (dipoler) som foretrekker å omgi seg med andre vannmolekyl i stedet for å slippe til andre stoff.

Elever som tenker vil ofte få problemer i forhold til språkbruken
som på den ene siden sier at tilsetting av såpe svekker overflatehinnen. Samtidig vet
vi at det er tilsetting av såpe som erfaringsmessig må til
for å lage store og "sterke" såpebobler. Mange vil da oppfatte ei stor såpeboble som et
eksempler på en sterkere hinne. Et aktuelt spørsmål i denne sammenhengen er
da om såpeboblene
blir sterkere jo svakere overflatehinnen er? Hvor er logikken?
Hvis man i stedet for å fokusere på hinnen, sier at bindingskreftene
mellom vannmolekylene blir svakere når man tilsetter såpe, så
er det forståelig at kreftene som sørger for sammenklumping
til dråper blir mindre og da blir det samtidig lettere å forme de
tynne hinnene i luftboblene.
Denne siste forklaringen kan da også lett brukes for å forklare
hvorfor "såpebåten" til venstre går framover. Figuren viser en papirbit
formet som en båt som befinner seg på rent vann og den grønne
flekken er da litt såpe. Der hvor såpen får kontakt med vannet
vil bindingskreftene mellom båten og vannet reduseres mens de er like
sterke i den andre enden. Vi bør da si at det er vannmolekylene i fremre
enden av båten som drar båten framover og ikke at det er vannmolekylene
omkring såpen som skyver båten framover. Det er med andre ord en
ubalanse mellom to krefter som medfører at båten går framover.
Vann er et løsemiddel
-Vann kan løse opp ulike stoff
(salt, sukker, skit, leire..)
Merk at å løse opp stoff vanligvis innebærer
at man blander stoffet med vann. Rent logisk innebærer det at vi binder stoffet
til vann. Man løser derimot stoffene fra der hvor det tidligere
bvar bundet som f.eks. gulv eller annet om vi vasker rent ved hjelp
av vann. Siden vann er
en dipol vil det kunne trenge inn mellom gulvet og skiten og løse opp
bindingene. Denne evnen til å trenge inn øker ofte om vi tilsetter
såpe til vannet.
-I
mange sammenhenger er det et ønske å skille fra hverandre de ulike
stoffene som er løst opp i vann. Her følger en liste over metoder
som kan brukes for å skille vann fra
andre stoff eller å skille andre stoff fra vann
Sedimentering
Om man fyller sølevann i et glass og lar det stå noen dager vil
man kunne oppleve at vannet vil se relativt rent ut øverst, mens man på bunnen
får ulike lag hvor både massetetthet og partikkelstørrelse har betydning for
hvor de ulike stoffene har havner. Generelt vil store og tunge partikler havne
nederst mens små partikler med liten tetthet vil havne øverst i sedimentlaget
man får på bunnen.
Krystallisering
Et eksempel på krystallisering er det som skjer når vi fordamper saltvann.
Det blir da dannet såkalte krystallstrukturer som da er restene som er igjen
når vannet har fordampet.
Filtrering
Ved hjelp av et kaffe-filter er det enkelt å demonstrere filtrering av forurenset
vann. Merk at det da bare er de minste partiklene som slipper gjennom filteret.
Destillering
Destillering handler å som å skille væsker fra hverandre fordi de har ulikt
kokepunkt. Eksempler er oljeprodukter, alkohol og vann. Figuren til venstre
er hentet fra en aktivitetsbok og den skal da illustrere destillering. Det er
da vanndamp som kommer ut fra tuten til kaffekjelen, og om man ønsker å tilbakeføre
denne til rent vann trenger man et kaldt reservoar som kan ta imot energi. Så
lenge skjeen er kald kan vi nok observere at det dannes vanndråper på denne,
men når den er blitt varm vil det ikke lenger skje noe særlig kondensering slik som
figuren antyder og figuren er derfor misvisende.