Varmelærens historie

(Ikke ferdig)

Begrepsoppklaring - energi og varme

Energi er i dag et generelt begrep som inkluderer varme og innledningsvis er det nyttig med en generell begrepsoppklaring. Generelt kan vi si at naturen består av to grunnstørrelser, stoff og energi. Stoff er da alt som er oppbygd av elementærpartikler (elektroner og protoner). I historisk sammenheng har man da diskutert om stoffet har vært oppbygd av noen minste udelelige partikler, og så langt viser da erfaringen at protonene og elektronene er udelelige partikler og vi kan derfor betrakte dem som byggesteinene i alt stoff. Energi er da en annen grunnstørrelse i naturen, og her vil vi da understreke at energi er noe annet enn stoff. Rent språklig skiller man ofte ikke klart mellom energi og stoff, og det er nok en hovedårsak til endel forvirring omkring hva som ligger i begrepet energi. Vi kan f.eks. si at ved eller bensin er energi, mens man vel egentlig burde sagt at det er snakk om stoff som inneholder kjemisk energi.  

Første gang vi vet at ordet energi er brukt er i  Merriam-Webster Collegiate Dictionary fra 1599, men betydningen var da mindre presis enn den vi bruker her. Ordet varme er ellers grunnleggende i alle språk. Innholdet i dette begrepet har nok variert litt, men vi kan vel regne med at det alltid har vært knyttet opp mot varmekilder som sol, ild ol. Den første som vi vet prøvde å systematisere en naturforståelse var Aristotle (384-322 f.Kr.) og han foreslo da at naturen bestod av 4 element: jord, vann, luft og ild. De tre første vil vi i dag karakterisere som stoff, mens den siste er da energi. I denne sammenhengen er det verd å legge merke til at begrepet 'ild' også omfattet det vi i dag kaller varme, lys, og 'vis viva' (livskraft).

Etter at Galileo Galilei (1564-1642) begynte å bruke termometeret ble det aktuelt å skille mellom temperatur og varme. Det var ellers i forbindelse med at James Watt og andre (1736-1819) utviklet de første moderne dampmaskinene hvor man brukte varme for å få utført ulike typer arbeid at man fikk behov for å skille mellom begrep som varme, arbeid, kraft og energi. Her vil vi da kort understreke at disse nye begrepene alle hører med i energi-delen av naturen og i det følgende vil i gjennom et historiske tilbakeblikk prøve å skape en forståelse for bakgrunnen til disse begrepene.

Varmens historie

Temperatur
Fra tidenes morgen har mennesker opplevd mer eller mindre varme. Bruk av ild til oppvarming og tilberedning av mat har vært kjent gjennom hele historien. Generelt er da varme noe det kan være mye eller lite av. I den tidligste historien hadde man ikke noen vanlig skala for hvor varmt det var i ulike sammenhenger, men det er vel sannsynlig at man brukte begrep som "kok-varmt" og "is-kaldt" ol. En hendelse som på en måte startet en ny epoke i varmens historie var oppfinnelsen av termometeret. Ingen vet med sikkerhet som laget det første termometeret. Et termometer er da er instrument som måler temperatur (ikke varme), og etterhvert ble det da klart at varme og temperatur var to ulike ting. 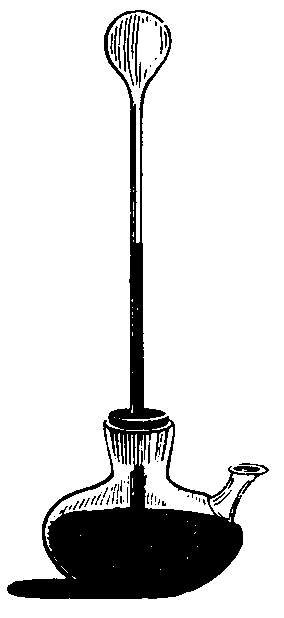Sannsynligvis er det mange som har utviklet ulike enkle termometer, men det er da Galileo Galilei (1564-1642) som har fått æren for å ha oppfunnet termometeret.  Til høyre vises et termometer som Galilei har laget. Ved siden av er det vist et termometer som en av hans elever laget i år 1600. Det var av glass og inneholdt sprit og skalaen var nien glasskjumper som var festet til røret. 

 "Galilei tok et glasskar som var formet som et hønseegg og trekt ut i et glassrør som var så tynt som et strå og to fingerspenn langt. Han varmet glasskula i handa, og så stakk han det tynne røret så vidt ned i et kar med vann. Etter hvert som glasset ble kaldt steg vannet i røret. Galilei brukte instrumentet til å undersøke graden av kulde og varme." Dette skrev en student etter å har hørt en forelesning av Galilei i 1603. Termometeret brukes også i dag i forbindelse med kvantifisering av varme, men her vil vi understreke at termometeret ikke gir noe direkte mål for hvor mye varme (energi) vi har et bestemt sted. Vi kan f.eks. oppholde oss i en badstu med 100°C uten å bli skadet, men vi vil raskt få forbrenning om vi holder hånda ned i vann med 60°C. Generelt kan vi si at vann kan inneholder mer varme enn luft (har større varmekapasitet) og temperatur er derfor ikke et direkte mål for varme.

Lufttrykk
I naturen er det en grunnleggende sammenheng mellom varme og trykk, og for at vi skal forstå begrepet varme er det nødvendig å ha kjennskap til begrepet trykk. 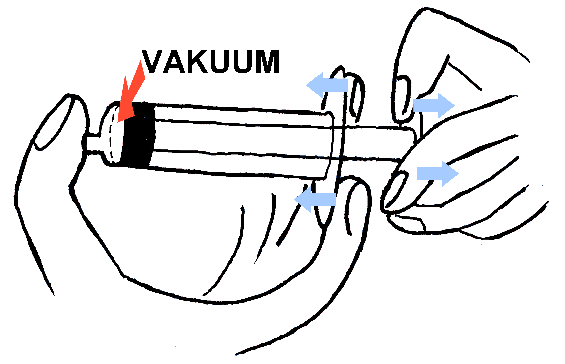Her følger derfor noen historiske høydepunkt i forbindelse med hvordan man oppdaget lufttrykket. Helt fra Arestoteles' tid har man observert krefter som motvirker at det vi kaller vakuum (= totalt tomrom), og man tenkte seg da at naturen har en slags iboende motvilje mot tomrom. Nå kan man tenke seg mange ulike forsøk som viser dette. Det mest overbevisende forsøket man kan gjøre i skolen er vel å bruke en engangsprøyte. Om vi presser den sammen, og så prøver å dra den ut samtidig som vi tetter hullet med fingeren, vil vi føle krefter som motvirker forsøket vårt på å lage et tomrom inni sprøyta som da ikke inneholder luft. Når vi skal prøve å forstå årsaken til dette kan man enten konsentrere oppmerksomheten om tomrommet og si at naturen unngår vakuum, eller så kan man konsentrere oppmerksomheten om omgivelsene og innføre et nytt begrep som kalles lufttrykk.

Oppdagelsen av det nye begrepet lufttrykk skjedde i flere steg. Et viktig steg var det italieneren Torricelli som stod for da han nærmest med en tilfeldighet oppfant barometeret og oppdaget at nivået til kvikksølvsøylen kunne variere over tid. Han brukte kvikksølv fordi det er en tung væske. Når han fylte denne væsken i glassrør og snudde disse opp-ned oppdaget han at  nivået til kvikksølvet alltid ble i underkant av 80 cm (800mm). Over kvikksølvet var det da vakuum. Ovenfor til venstre vises et kvikksølvbarometer som fortsatt i dag brukes til å måle lufttrykk. Problemet for Torricelli og hans samtidige var å forklare hvorfor barometeret virket som det gjorde.  

 Det er da franskmannen Pascal som har fått æren for å forklare årsaken til lufttrykk. Han reiste rundt og gjorde målinger med gi et kvikksølvbarometer og et kvikksølvtermometer, blant annet i Paris og på toppen av fjellet Puy-de-Döme. Det at lufttrykket bli lavere jo høyere over havet man kommer, var da at et bevis på at det er luften eller atmosfæren rundt jorda som skaper lufttrykket. Lufttrykket har med andre ord sammenheng med hvor mye luft det er over der vi måler lufttrykket. Denne mengden luft vil da kunne variere litt over tid og det er da årsaken til at vi måler høytrykk og lavtrykk ved hjelp av et barometer.

Det er videre slik at luft og andre stoff utvider seg nå de blir varme, og om ikke det er plass for denne utvidelsen vil trykket øke. Om vi f.eks. varmer opp luften i en "tom" beholder med luft i etter at vi har satt på korken, vil vi kunne erfare at det blir et overtrykk i beholderen (høyere trykk enn på utsiden). Dette kan f.eks. bli så stort at korken spretter ut. Dette var da ting man var klar over på denne tiden, men folk flest var da ikke så opptatt av å formulere ulike naturlover utfra slike erfaringer. Men noen var mer nysgjerrige enn andre og her vil vi nevne noen som gjorde ulike forsøk som har med varme å gjøre og vi vil da nevne de lovmessighetene de kom fram til.

Tilstandslikningen

 Her vil vi først nevne sammenhengen mellom trykk og volum som gjelder tilnærmet for luft og andre gasser. Den aktuelle lovmessigheten er kalt Boyles lov og den sier da rett og slett at trykk og volum er omvendt proposjonale størrelser (p·V=konstant). Alle vet f.eks. at trykket øker når vi klemmer sammen luft, men han viste da at det var en enkel matematisk sammenheng mellom disse størrelsene som gjør praktiske beregninger relativt enkle samtidig som den på en måte også "ber" om en forklaring. Denne forklaringen er da hovedproblemet som vi ønsker å  belyse her. Det finnes med andre ord ulike forklaringer på denne sammenhengen, og Boyle var vel den første som beskrev ulike gassmodeller som kunne forklare denne sammenhengen.

Det er videre en sammenheng mellom temperatur og trykk/volum til en gass (p=kT eller V=kT) og denne er da kalt Gay-Lussac-lov etter en fransk kjemiker som gjorde endel målinger med ulike typer gasser. At gasser utvider seg når de blir oppvarmet var ikke noe nytt, men det nye var at man fikk gode data som på en klar måte viste sammenhengen mellom temperatur og volum/trykk som var det viktige. Boyles og Gay-Lussac's lov kan videre kombineres til den såkalte  tilstandslikningen for idialgass som f.eks. kan skrives på formen:

PV=konstant·T

Merk at T her står for absolutte temperaturen (Kelvin) og den forteller da f.eks. at trykk(P) eller volum(V) vil dobles om temperaturen dobles. Om temperaturen derimot holdes konstant vil trykket halveres om volumet dobles. Merk ellers at denne formelen bare gjelder for en idialgass. Dette betyr at den bare gjelder tilnærmet for virkelige gasser, men den er da nyttig for å anslå hva som skjer i praktiske situasjoner.

To ulike gass-modeller

I vitenskapelig sammenheng er man vanligvis ikke fornøyd med bare å beskrive ulike forhold. Man ønsker også å forstå hvorfor naturen oppfører seg som den gjør. I dette tilfellet er det da snakk om å finne fram til modeller som kan forklare de egenskapene som vi finner i naturen. I den aktuelle vitenskapelige perioden diskuterte man to ulike forklaringsmodeller som er basert på hvert sitt prinsipp. Boyle satte da to modellene opp mot hverandre. På den ene siden kunne man betrakte trykk som forårsaket av fraskyvingskrefter, og denne modellen var blant annet foreslått av Isaac Newton(1642-1727). På den andre siden kunne man tenke seg at trykk var forårsaket av gjentatte elastiske støt fra partikler som var i stadig bevegelse. (http://www.math.umd.edu/~lvrmr/History/EarlyTheories.html)  

1 Kalori-modellen Denne modellen, som var mest populær fram til 1800-tallet, gikk da ut på at man betrakte luft som partikler som hadde en innbyrdes fraskyvning overfor hverandre. Isaac Newton utviklet f.eks. en matematiske modell som kunne forklare årsaken til lufttrykk. Varme ble i denne modellen betraktet som en slags "fluid" eller energi i en "eter" som befant seg mellom partiklene. Denne energien ble også kalt "Caloric". Når man så definerte temperatur som tetthet av varme (varme/volum), kunne man også forklare Gay-Lussac's lov. Modellen kunne videre forklare lyd, diffusjon (f.eks. lukt som sprer seg i luft), energi i faseoverganger, varmekapasitet (ved å postulere at energi også kunne lagres inni luftpartiklene) og andre daglige fenomen på en grei måte. Den fikk imidlertid problemer med å forklare noen forsøk av Gay-Lussac som viste at når gass ekspanderer fritt (i vakuum i stedet for å presse på et stempel), så observerte man ingen (egentlig svært liten) endring i temperatur. Dette er en hovedårsak til at den sjeldent nevnes i dagens lærebøker.

2 Kinetisk gassteori  Kjernen i denne modellen er at trykk og temperatur er direkte knyttet opp mot bevegelser i de partiklene som utgjør gassen. Her vil vi da understreke at det er snakk om bevegelser av selv gasspartiklene som utgjorde varmen og ikke bevegelser i eller omkring dem. Sannsynligvis har man til alle tider tenkt seg at varme er en form for bevegelse siden varme f.eks. kan bryte opp ulike bindinger på ulike nivå. Også de som argumenterte for Kalori-modellen tenkte seg at varme var en form for bevegelse men denne foregikk da i hovedsak mellom partiklene og delvis også i dem i det mediet man kalte eteren.
Det var den sveitsiske matematikeren Daniel Bernoulli (1700-1782) som utviklet det matematiske grunnlaget for denne modellen. Han viste f.eks. at trykket vil dobles om volumet halveres (Boyles lov) om vi antar at trykket er forårsaket av luftpartiklenes stadige støt mot omgivelsene. Videre viste han at om vi antar at varme-energien i luft egentlig er den kinetiske energien til luftpartiklene (E_k=½mv²), så vil man også få den kjente sammenhengen mellom temperatur og trykk (Gay-Lussac's lov). Jo fortere luftpartiklene beveger seg, jo flere og kraftigere støt blir det mot veggene og tilsynelatende hadde man kommet fram til en enkel varmemodell som kunne forklare begge de viktigste lovmessighetene som gjelder for luft og andre gasser. ()
En måte å anskueliggjøre hvordan Bernoulli påviste at tilstandslikningen følger av kinetisk gassteori, er å tenke seg en engangsprøyte med luftpartikler inni. Gassen i denne sprøyta vil da bestå av mange partikler. I prinsippet er da trykk og temperatur forårsaket av mange luftpartikler som hver bidrar like mye, og derfor er det mulig å forenkle totalbildet og tenke seg en partikkel som spretter fram og tilbake mellom stempelet og bunnen av sprøyta. Om vi så presser stempelet inn slik at volumet blir halvert, så vil avstanden som partikkelen beveger seg mellom støtene bli halvert og antall støt pr tidsenhet på veggene vil da bli fordoblet. Dette illustrerer da hvordan sammenhengen mellom trykk og volum kan forklares ved hjelp av kinetisk gassteori. Om vi i stedet varmer opp gassen til dobbel temperatur (ifølge Kelvin-skalaen) forteller tilstandslikningen at trykket vil bli doblet. Modellen forteller da at hastigheten til gasspartiklene økes med Ö2, som da medfører at antall støt mot veggene også øker med Ö2. Trykkøkningen som da er et resultat av at både farten til partiklene øker og antall partikkelstøt pr tidsenhet øker, vil da øke med Ö2·Ö2=2 som da betyr en dobbling av trykket når temperaturen dobles.

Problem som sjeldent nevner i moderne lærebøker

I dag er det en vanlig oppfatning at kinetisk gassteori ble allment akseptert på 1800-tallet og at man i dag kan regne den som et slags vitenskapelig faktum som ikke lenger diskuteres. Her vil vi da bare påstå at dette ikke er tilfelle og vi vil da her kort nevne noen av de argumentene som er blitt fremsatt mot modellen.

1 Gjelder bare for gasser (ikke væske og fast stoff)
En hovedgrunn til at mange var skeptisk til denne modellen var da at den var lite oppklarende i forhold til hvordan man skulle forklare varme i væsker og faste stoffer som da også kan ha en temperatur i likhet med gasser. Ifølge kinetisk gassteori er det en grunnleggende antakelse at det ikke er vedvarende krefter mellom partiklene i gassen (krefter kun i kollisjonsøyeblikket). På den andre siden er det åpenbart for alle at det må være kontinuerlige krefter mellom de partiklene som inngår i væsker og faste stoff. I litteraturen er det lite snakk om dette problemet siden man vanligvis behandler gass, væske og faste stoff i ulike kapitler. Men det representerer likevel et problem for dem som ønsker seg en forståelig modell av hva varme er som gjelder i alle typer stoff.

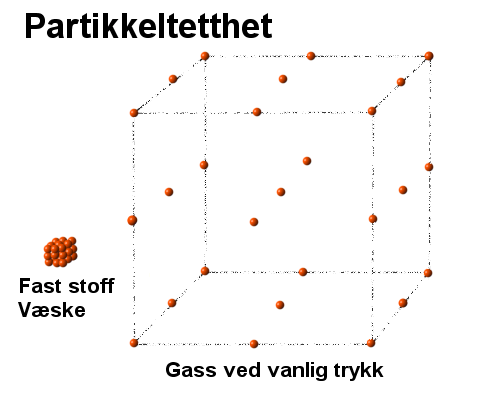2Vanskelig å anslå størrelsen på gasspartiklene
Siden tettheten til vanlige gasser er ca. 1/1000 del av tettheten til vanlige stoff og væsker, så betyr det at avstanden mellom partiklene blir i gjennomsnitt 10 ganger større når væske eller fast stoff går over i gassform. Et visuelt bilde av dette er vist til høyre hvor det er vist like mange partikler som fast stoff/væske og som gass. Ifølge en nettartikkel (http://www.math.umd.edu/~lvrmr/History/Revival.html) så var det Tyskeren Rudolf Clausius (1822-1888) som var en av hovedpersonene bak kinetisk gassteori. Han foreslo da at  varmen i gasser var ensbetydende med at gasspartiklene som er vist til høyre hadde en gjennomsnittshastighet i størrelsorden 500m/s (=1800km/h) ved vanlige temperaturer. Han tenkte seg videre at partiklene var så små at antall kollisjoner mellom partikler var neglisjerbare i forhold til antall kollisjoner med veggene i beholderen. Disse antakelsene gav da tilstandslikningen som er vist foran. Han fikk relativt liten gjennomslag for denne "dramatiske gassmodellen" da den ble presentert. Kollisjoner med så høye hastigheter som 1800km/h er ganske dramatisk om man prøver å forestille seg hva det innebærer rent fysisk. Hovedårsaken til at man var skeptisk til modellen var nok at den virket vel fjern fra den praktiske virkeligheten.  Den nederlanske metorologen C.H.D. Buys-Ballot påviste f.eks. at den harmonerte dårlig med hva vi erfarer når det f.eks.gjelder diffusjon eller spredning av luktstoffer i luft. Om vi f.eks. slipper ut en sterkt lukt i den ene enden av et rom går det en viss tid før de aktuelle luktpartiklene kan luktes i den andre enden av rommet. Om luftpartiklene i rommet virkelig oppførte seg slik Clausius foreslo, så burde spredningen av lukt gå mye raskere.
Claudius svar på denne innvendingen var da at han gikk bort fra antakelsen om at luftpartiklene var små. I denne sammenhengen kan man da definerer størrelsen på en partikkel til å være lik minimumsavstanden mellom sentrum til to partikler som "kolliderer". Når det f.eks. gjelder to kuler som er opphengt i en snor, så vil størrelsen da være lik diameteren til kulene. Men om vi lader begge kuler med samme ladning, kan vi oppleve at fraskyvingskreftene mellom dem gjør at de ikke vil berøre hverandre ved et lett "sammenstøt" og i dette tilfellet vil da de elektriske fraskyvingskreftene gjøre at størrelsen på kulene vil bli større enn den synlige diameteren. I stedet for å snakke om størrelsen på partiklene snakker man oftest om gjennomsnittlig fri bevegelse (mean free path), men det er da bare "minusverdien" til størrelsen (størrelse+gjennomsnittlig fri bevegelse=konstant) og de handler da om det samme. Poenget her er da at det var og er et grunnleggende kjennetegn på kinetisk gassteori at tiden som partiklene påvirker hverandre innbyrdes er relativt liten (neglisjerbar). Om man f.eks. tenker seg at det er en fraskyvingskraft mellom luftpartiklene som gjør partiklene større, så er det ikke lenge før man er tilbake til calori-modellen som kinetisk gassteori egentlig skulle erstatte. Her vil vi da bare kort si at det er mulig å få samsvar mellom diffusjon i luft (spredning av lukt ol.)  og kinetisk gassteori, ved å øke størrelsen på luftpartiklene, men man bør da samtidig innrømme at det finnes fraskyvingskrefter mellom gasspartiklene som har en viss rekkevidde og man bør vel også si noe om hva slags krefter det her er snakk om. Hittil synes det som om man har ignorert dette problemet fordi kinetisk gassteori egentlig ikke fungerer i praksis (bare i teorien).

3 Tiltrekningskrefter mellom gasspartiklene?
Når partikler støter elastisk sammen må det nødvendigvis være noen fraskyvingskrefter som forårsaker at partiklene spretter tilbake når de kolliderer. Det er imidlertid sjelden at de som bruker kinetisk gassteori nevner noe om disse kreftene. Årsaken til dette er sannsynligvis at det ifølge kinetisk gassteori er tiltrekningskrefter og ikke fraskyvingskrefter mellom gasspartiklen! Hvordan har man så kommet fram til den konklusjonen? Som nevnt tidligere gjorde Gay-Lussac forsøk hvor konklusjonen var at gass som ekspanderte adiabatisk ikke fikk endret temperaturen slik som kalori-modellen forutsa. Denne observasjonen var da slik man skulle forvente om kinetisk gassteori var rett. Adiabatisk ekspansjon er da fri ekspansjon uten mottrykk. Vet en slik ekspansjon utfører ikke gassen et arbeid på f.eks. et stempel. Problemet var at denne konklusjonen fikk en relativt kort "levetid". Joule og Thomson (som senere ble kalt Lord Kelvin) gjorde omkring 1850 noen mer nøyaktige forsøk med adiabatisk ekspansjon av gass og fant da at man i slike tilfeller vanligvis fikk en avkjøling. Ikke så mye som kalori-modellen forutsa, men nok til å skape problemer for kinetisk gassteori. Den aktuelle effekten kalles i dag Joule-Thomson-effekten og her følger et par sitat fra noen oppslagsverrk:

Ifølge kinetisk gassteori er temperaturen et uttrykk for hastigheten til gasspartikler og om man slipper slike gradvis gjennom et lite hull fra et område med mange luftpartikler (stort trykk) til et område med få luftpartikler (lite trykk) så skulle farten være bevart og dermed skulle også temperaturen forbli uforandret. Det var da ikke dette man observerte!. Men i stedet for å sette spørsmålstegn med kinetisk gassteori, så er det i dag vanlig å si at det ikke finnes det vi kan kalle en idealgass. Man vet f.eks. at tilstandslikningen for en idealgass bare gjelder tilnærmet for virkelige gasser, og derfor tenkte man vel bare at denne observasjonen var et nytt eksempel på at kinetisk gassteori gav et tilnærmet rett bilde av virkeligheten. Problemet i dette tilfellet var imidlertid at det var snakk om målbare temperaturendringer som innebar endring av energiforhold og denne energi- forskjellen måtte forklares på en eller annen måte. Forskjellen mellom de to områdene var da tettheten av molekyler og om man antok at det var en liten tiltrekningskraft mellom gassmolekylene som ble "motvirket" når gassmolekylene spredte seg fra hverandre, å kunne det forklare hvor energitapet (det som viste seg som lavere temperatur) ble hen (svarer til å løfte en stein i et gravitasjonsfelt). Derfor kan man i noen sammenhenger lese at Joule-Thomson forsøket viser at det er tiltrekningskrefter mellom gassmolekylene. Det er altså ikke snakk om krefter man har observert i praksis, men det er snakk om krefter man trenger for å bevare kinetisk gassteori. De fleste som tenker litt vil vel reagere på at de bare hører om tiltrekningskrefter og ikke frastøtingskrefter i gasser. All erfaring viser nemlig at gassmolekylene vil bevege seg fra hverandre om de får anledning, og det er da nærliggende å tenke at gasspartiklene opplever gjensidige frastøtingskrefter og ikke tiltrekningskrefter som det står om i mer avanserte fysikkbøker.

4 Varmekapasitet
Ulike stoff kan lagre mer eller mindre energi/varme både i forbindelse med oppvarming/avkjøling og i forbindelse med faseoverganger fast stoff/væske/gass og i denne sammenhengen hadde kinetisk partikkelmodell lite å bidra med, når det gjaldt å forstå dette. "The caloric theory could also explain phenomena such as the latent heat of phase transitions (solid to liquid or liquid to gas) and the heat absorbed or released in chemical reactions, by postulating that some caloric is "bound" to the individual atoms or compounds. The ordinary pressure-volume relations of gases are determined by the unbound or "free" caloric that fills the space between particles. The kinetic theory seemed to offer no plausible account of these phenomena, ..." ( http://www.math.umd.edu/~lvrmr/History/EarlyTheories.html)

5 Lyd
Lyd er ellers et fenomen som sprer seg gjennom gasser, væsker og faste stoff og i den sammenhengen utviklet man matematiske modeller som kunne forklare ulike lydfenomen. Disse modellene var da basert på at man tenkte seg at det fantes krefter mellom molekylene/atomene som formidlet lyden, og mykheten i kreftene (compressibility/elasticity) og treghet i mediet (inertia) bestemmer f.eks. farten til en lydbølge. Kinetisk partikkelmodell på side skapte bare forvirring i forhold til det å forstå lyd, og derfor var det få som jobbet med praktisk fysikk som aksepterte kinetisk partikkelmodell da den ble presentert. "Finally, the caloric theory gained credibility in the early 19th century from Laplace's use of it to calculate the speed of sound in gases, resolving a long-standing discrepancy between theory and observation; and it was indirectly supported by the acceptance of the particle theory of light, since light and heat were widely viewed as qualitatively identical phenomena." ( http://www.math.umd.edu/~lvrmr/History/EarlyTheories.html)

Brownske bevegelser

I noen sammenhenger kan man få det inntrykket at oppdagelsen til Robert Brown i 1827 beviser kinetisk partikkelmodell: "I 1827 gjorde den skotske botanikaren Robert Brown (1773-1858) ei oppdaging som kunne ha stadfesta molekylhypotesen. Brown hadde pollen i vatn, la ein drope mellom to glassplater og såg på dråpen i eit mikroskop. Til si store undring såg han at pollenkorna ikkje låg i ro, men rugga på seg. Først 80 år seinarer skjøna ein at det var fordi pollenkorna vart bombarderte av vassmolekyl.." (Ergo 2FY s 165 Aschehaug 1997) 
"It was at the end of the 19^th century that the French physicist, Jean Perrin came forward with the exact description; his experiments on Brownian motion brought the scientific proof of the kinetic heat theory..."  (http://www.ujf-grenoble.fr/ismrm/Diffusion/diffusion_historical_outline.htm)

Før vi vurderer disse påstandene, så vil vi kort se litt nærmere på hva Robert Brown (1773-1885) egentlig gjorde.  Han var født i Skottland, var utdannet lege, men brukte hovddelen av sitt liv på å studere biologi. Han var f.eks. med på en ekspedisjon til Australia og hadde med seg ca 4000 planter hjem til England. Han brukte senere mye tid på å studere planter i mikroskop og til venstre er det vist et bilde av mikroskopet hans. (lånt fra http://www.sciences.demon.co.uk/wbbrowna.htm) Brown gjorde blant annet endel grunnleggende observasjoner av ulike typer planteceller. Han er imidlertid mest kjent for å ha oppdaget de såkalte brownske bevegelser og det skjedde da i forbindelse med et studium av pollen. Han observerte da at pollen som var oppløst i vann, enten det gjalt nytt pollen eller pollen som var oppbevart 11 måneder i en alkoholløsning, utførte små kontinuerlige bevegelser. Selv mennesker som observerer disse bevegelsene i vår tid, har trodd at de ser er en slags grunnleggende form for liv. Brown, som da ikke var den første som observerte disse bevegelsene, har da fått navnet sitt knyttet til dem fordi han på en overbevisende måte konkluderte at det var snakk om bevegelser som måtte ha en fysisk forklaring og ikke en biologisk forklaring. Disse brownske bevegelsene kan man også observere når man studerer røykpartikler i gass og de ble da senere brukt som et viktig argument for kinetisk partikkelteori da denne ble lansert. Men er det egentlig et bevis for at gassmolekylene har så høye hastigheter som denne teorien forteller? De som bruker disse bevegelsene som bevis for kinetisk gassteori, nevner sjeldent noe om at det også finnes slike bevegelser i væsker. Det er med andre ord vanskelig å tenke seg at det er samme mekanisme som forårsaker disse bevegelsene i de to mediene. Her vil vi imidlertid understreke at det ikke er snakk om bevis i vitenskapelig forstand, siden det også er mulig å tenke seg andre mekanismer som ligger bak de aktuelle bevegelsene.

EM-modellens forklaring av Brownske bevegelser En mulig mekanisme bak disse bevegelsene er at de er forårsaket av elektroner som spretter ut fra atom/molekyl med en høy hastighet. Radioaktiv b-stråling er f.eks. elektroner med svært høy hastighet som man regner med kommer fra atomkjerner, og det er da naturlig å tenke seg at elektroner som blir løsrevet lenger ute vil ha mindre fart, men slike løsrivelser vil da kunne forekomme desto oftere.

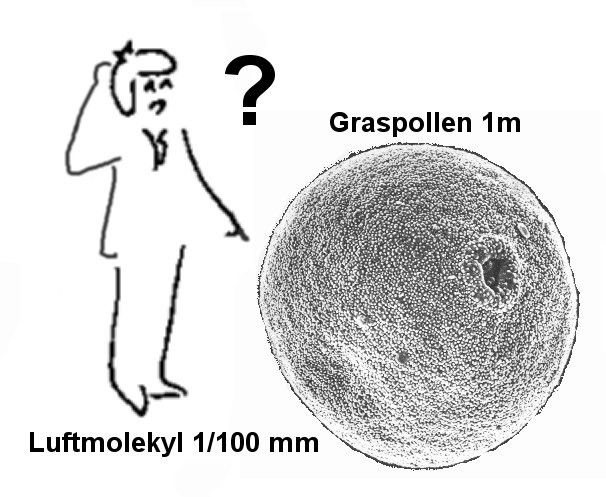Her kan det ellers være interessant å prøve å danne seg et bilde av størrelsesforholdet mellom pollenkorn som er i størrelsorden 10-100 mm (10^-5-10^-4m) og gassmolekylene på den andre siden som er i størrelsorden 10^-10m og har en innbyrdes avstand omkring 10^-9 m. Om vi tenker oss en skalamodell hvor et gresspollen har en diameter på 1 m. så betyr det at gasspartiklene vil få en størrelse på 1/100 mm (10^-5 m) (som virkelig pollen) og når disse gasspartiklene kolliderer med det "store" graspollenet, så vil tettheten være i størrelseorden 1/10 mm (10^-4m). De som har sett brownske bevegelser i praksis, vil i denne sammenhengen få store problemer med å forestille seg at så små gassmolekyler i så store mengder vil forårsake de store bevegelsene som pollenpartiklene virkelig har. Her vil vi da konkluderer med at det sannsynligvis er de som ikke har satt seg inn i hva det handler om som mener at brownske bevegelser er et bevis for kinetisk gassteori.

Hva med forsøk som tydelig viser gasspartikkelhastigheter?

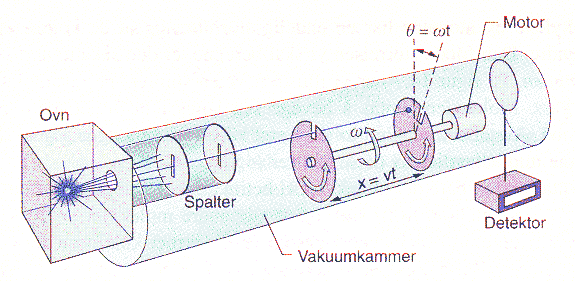I tillegg til Brownske bevegelser er det vel forsøkene som viser hastighetsfordelingen til gasser av metaller, som har overbevist flest mennesker om at kinetisk partikkelmodell er bevist. I slike forsøk observerer man jo at atomene har en viss hastighet på en direkte måte, og da er det vel heller ikke noen grunn til å tvile på at gassmolelylene i vanlige gasser har tilsvarende hastigheter. Til venstre er vist en prinsippskisse fra et slikt forsøk (Lillestøl, Hunderi, Lien: Generell fysikk s.55 Univ. 2001) Under vises så det opprinnelige forsåket som da ble brukt for å bekrefte kinetisk gassteori.

"The original molecular beam experiment to directly measure molecular speed was done by Stern in 1920.  His apparatus used a rotating cylinder, rather than two rotating disks.  The metal vapor was produced by heating a silver wire." (http://www.carlton.paschools.pa.sk.ca/chemical/KineticEnergy/TempAndKE.htm

Siden har man så gjort flere slike forsøk og i tilhørende tekstbeskrivelser kan man da ofte lese at dette forsøket bekrefter Maxvells hastighetsfordeling for gasser. Det man fant var altså en slags normalfordeling av hastigheten til metallmolekylene som ble sendt ut fra ovnen. Her er det imidlertid verd å merke seg at selv om man snakker om en gasstilstand for de aktuelle atomene, så er det ikke snakk om vanlig gass i det aktuelle området. For at metallatomene (f.eks. Cadmium) skal fortsette å bevege seg etter at de er kastet ut fra den varme ovnen må det være lufttomt i beholderen. Dessuten er det snakk om langt lavere hastigheter enn de man antar finnes i vanlige gasser. Det er altså snakk om helt andre forhold enn man har i vanlige gasser, og følgelig kan man ikke bruke dette eksperimentet som argument for kinetisk gassteori. Eksperimentet viser da bare at hastigheten til atomer som løsrives fra en varm overflate vil få hastigheter med en bestemt variasjon og det er da den samme variasjonen man antar at gassmolekylene i luft har. Problemet i denne sammenhengen er imidlertid at de som presenterer disse forsøkene ofte unngår å  nevne det som skiller forsøkene fra de forholdene man antar finnes i vanlige gasser, og det etterlater da et inntrykk av at man har sett at gassmolekyler virkelig beveger seg med høye hastigheter slik kinetisk gassteori sier.

Praktiske varmemålinger

Når man studerer et fenomen, kan man bruke en av to tilnærmingsmåter. En måte er å konsentrere seg om å utvikle modeller av det vi prøver og forstå og så teste om disse modellene forutsier hva som skjer i praktiske forsøk. Denne tilnærmingsmetoden er en slags fellesnevner for det som er nevnt så langt. På den andre siden er det nok vel så mange som har valgt å utvikle en varmeforståelse som er mest mulig nyttig i forbindelse med å takle praktiske forhold på en fornuftig måte. I denne sammenhengen er det da f.eks. snakk om å kunne gjenta handlinger som har gitt nyttige resultat og i slike sammenhenger er måling viktig. Det er f.eks. snakk om å måle hvor mye stoff (masse/volum), varme eller temperatur som gir optimale forhold i ulike sammenhenger. Eksempler på sammenhenger hvor det er nyttig å kunne noe om varme er oppvarming av hus, matlaging og produksjon av ulike stoff som er nyttige i ulike sammenhenger osv. Den vanligste måten å fremskaffe varme i gamle dager å forbrenne ting (omdanne kjemisk energi til varme), men det var også mulig å samle opp varme ting og overføre varmen mellom ulike stoff. I slike tilfeller er det naturlig å tenke på varme som noe som kan finnes inni ulike stoff eller solstråler. Denne varmen ble så overført mellom ulike stoff ved berøring. Den aktuelle varmen som fantes inni ulike stoff ble kalt kalori (caloric) og den aktuelle forestillingen fungerte bra i de fleste praktiske situasjonene. I en slik modell var da kalori noe som kom fra sola, gikk inn i planter, kom ut igjen og varmet opp stua når vi fyrte med ved før den til slutt forsvant gjennom dør og vegger når ilden sluknet. I en slik sammenheng kunne man da bruke "favner med ved", "sekker med kull", "timer i sola" eller liknende som mål for hvor mye kalori man trengte i ulike sammenhenger.

 Ifølge historiebøkene var det Benjamin Thomson som var den første som satte spørsmålstegn med om den tradisjonelle calori-modellen var rett, og bakgrunnen var da at han observerte boring av kanonløp. Det var da hester som drev boret slik figuren nedenfor antyder og i den sammenhengen ble det utviklet ganske mye varme. Arbeiderne måtte derfor ha vann på kanon og bor for å holde temperaturen nede. Problemet i dette tilfellet var å tenke seg hvor varmen kom fra. Ifølge kalorimodellen skulle man tro at varmen opprinnelig lå i kanonløpet og at den ble frigjort når boret skar av fliser. Dette fant Thomson ut måtte være feil og han argumenterte da for at varmen egentlig kom fra hestene gjennom den bevegelsen de overførte til kanonen. Et argument for dette var at varme bare ble utviklet når hestene arbeidet, og jo mer slitt boret ble, jo mer varme ble det utviklet. Tomson prøvde ellers å veie gjenstander når de var oppvarmet og avkjølet og siden han fant samme vekt, konkluderte han med at varme ikke hadde masse. Tomsons viktigste bidrag var imidlertid at han var en av de første som klart viste til det vi kaller "varmens mekaniske ekvivalens" (mecanical equialent of heat). Eksempelet med hester som borer kanonløp viser da tydelig at mekanisk arbeid kan omformes til varme og denne sammenhengen mellom mekanisk energi og varmeenergi er grunnleggende i mange praktiske sammenhenger. Om mekanisk energi kan omdannes til varme, så er det nærliggende å tenke at varme kan omdannes til mekaniske energi, og den teknologiske revolusjonen som fant sted omtrent på denne tiden, blant annet gjennom utviklingen av dampmaskinen (varme som omdannes til bevegelse), har sannsynligvis sammenheng med at man oppdaget forbindelsen mellom varme og mekanisk energi. ( http://www.hcc.hawaii.edu/hccinfo/instruct/div5/sci/sci122/newton/heat/cannonbore.html)

I forbindelse med bruk av dampmaskiner og annen teknologi hadde man behov for å finne ulike varmeverdier og i den sammenhengen har James Jule gitt et viktig bidrag som da har ført til at enheten for energi i ettertid har fått hans navn (Joule).  

 Joule brukte mye tid på å gjøre ulike forsøk hvor han overførte energi mellom ulike energiformer, for å finne noen konkrete tall som kunne gjøre at vi kunne sammenlikne energimengder fra ulike energiformer. Den viktigste tallet han fant var da det som gir sammenhengen mellom temperaturforskjeller og mekanisk arbeid. I praksis fant han varmekapasiteten til vann som med dagens benevninger er 4,18 J/kgK. Dette tallet forteller da hvor mye mekanisk energi man må tilføre 1 kg vann for å varme det opp 1 grad (K) og figuren under viser da det instrumentet han brukte for å finne dette tallet. Dette viser da en visp som står ned i en beholder med vann. Når loddene som henger på hver side beveger seg nedover vil de drive vispen rundt i vannet samtidig som de taper potensiell energi. Ved å anta at tapet av mekanisk energi i loddene er lik energiøkningen som følge av at vannet ble oppvarmet, så fant han da fram til det aktuelle tallet som er vist ovenfor. Når man på den måten har et tall som gir oss sammenheng mellom varmeenergi og mekanisk energi, kan man f.eks. gjøre ulike målinger av ulike typer motorer (dampmaskin ol.)og finne ut hvor gode de er til å utnytte tilført energi (virkningsgrad) og andre nyttige data.

Med bakgrunn i de tallene man fant for hvor mye energi som er involvert i ulike sammenhenger, så kunne man videre formulere ulike lovmessigheter som gjelder for varme. De mest kjente er temofysikkens første og andre hovedsetning. Den første forteller at totalenergien vil være bevart i alle energiomdanningsprosesser og den andre sier da noe om at energiomdanningene vanligvis ikke er reversible. Det vil med andre ord si at endel omdanninger bare kan gå en veg og det er da ikke mulig å komme tilbake til utgangspunktet.

Irreversible prosesser?

 Generelt kan vi si at Newton hadde lyktes med å forklarer mye av det som skjer på himmelen og på jorden med sin mekanikk-modell, og når noen foreslo å bruke den samme  modellen til å forklare alt som har med varme å gjøre, så dukket det opp et filosofisk problem som skapte endel debatt. Kinetisk partikkelmodell er i prinsippet et forsøk på å forklare temperatur og varme ved hjelp av mekanikk. I motsetning til vanlig mekanikk som da handler om relativt få gjenstander, så handler kinetisk gassteori om svært mange gjenstander/partikler og derfor bruker man her en statistisk tilnærmingsmetode. Kinetisk gassteori handler da om summen av mange enkeltstående hendelser som hver for seg kan beskrives med de begrepene Newton innførte og som hver for seg følger Newtons lover. De fleste er enige om at det er et mål å kunne forklare flest mulig fenomen med færrest mulige modeller og ideen om også å kunne forklare varmelæra ved hjelp av Newtons mekanikk er da positiv i seg selv. Tidligere har vi nevnt endel praktiske problem som dukket opp da man prøvde å forklare varme som et mekanisk fenomen. Her vil vi da kort nevne et mer grunnleggende teoretisk  problem som man ikke har funnet noen tilfredstillende forklaring på. Problemet er da kort fortalt at Newtons mekanikk er reversibel, men all erfaring forteller at varmeprosessene ikke er reversible. Når en prosess er reversibel, så betyr det bare at det i teorien er mulig å snu hendelsesforløpet når som helst i prosessen uten at det videre hendelsesforløpet blir "unaturlig". I prinsippet er det f.eks. mulig å snu jordas gang rundt sola og den ville da følge samme bane i motsatt retning. Det er med andre ord like naturlig for jorda å gå den ene som den andre veien. Når det gjelder varme har erfaringen vist at varmeenergien alltid vil gå fra et område med høyere temperatur til et område med lavere temperatur. Om den aktuelle varmen egentlig var elastiske partikler slik kinetisk gassteori sier, så skulle man forventet at om man et bestemt tidspunkt snudde hastighetene til alle partiklene, så ville alle partiklene følge samme spor tilbake. Om det da samtidig er snakk om et tilfelle hvor det skjedde en overføring av varme fra et varmt til et kaldt område, så ville den aktuelle omsnuingen føre til at varmen gikk fra det kalde til det varme området. Dette skjer da aldri i praksis og derfor var mange skeptiske til om kinetisk partikkelmodell kunne forklare fenomenet varme.

"Maxwell's demon"
Tyskeren Rudolph Clausius var på slutten av 1800 tallet en av hovedforkjemperne for kinetisk partikkelmodell. Engelskmannen James Maxwell er mest kjent for å utvikle en matematikk som beskriver elektromagnetiske fenomen (Maxwells likninger), men har var da også en viktig bidragsyter i forbindelse med å utvikle den matematiske modellen for kinetisk gassteori.

 Det fortelles så at Clausius skrev til Maxwell i 1867 og bad om hjelp i forbindelse med en lærebok i termofysikk han arbeidet med. ( http://www.math.umd.edu/~lvrmr/History/Irreversibility.html)

 Det var da i svaret på dette brevet man finner omtalen av den såkalte "Maxwell's demon". Ifølge litteraturen mente Maxwell at termofysikkens andre hovedsetning ikke var absolutt. Han mente da at det kunne tenkes tilfeller hvor man fikk energioverføring fra et kaldt til et varmt område. Han beskrev da to gassbeholdere med varm og kald luft og et hull mellom som kunne stenges og åpnes veldig raskt. Han beskrev videre en dørvokter (senere kalt maxwell's demon) som åpnet hullet og slapp gjennom raske partikler fra den kaldeste gassen og slapp gjennom langsomme partikler fra den varmeste gassen. Ellers ble partikler med normal hastighet i forhold til aktuelle temperatur hindret gjennomgang. Dette ville da føre til at man fikk overført energi fra den kalde til den varme beholderen. Dette eksemplet var vel ment å være et eksempel på at det er mulig å tenke seg unntak fra termofysikkens andre hovedsetning, men det viser da samtidig at man brukte relativt virkelighetsfjerne eksempler når man arbeidet med å utvikle kinetisk gassteori.   

Nå er det sikkert mulig å treffe mennesker som vil hevde at man kan finne begrunnelse for termofysikkens andre hovedsetning i de relativt avanserte statistiske matematiske modellene man bruker når man beskriver slike forhold. Her vil vi da bare kort nevne at enhver matematikk bygger på visse aksiomer og resultatet av de matematiske beregningeene blir ikke mer sikre enn de aksiomene man har lagt til grunn. I denne sammenhengen vil vi da kort gjenta at det er et problem når grunnlaget (Newtons mekanikk) er reversible prosesser, mens konklusjonene ikke er reversible.

EM-modellens begrunnelse for irreversibilitet Her vil vi ellers kort nevne at de aktuelle irreverible prosessene vi observerer i varmelære lett kan forklares om man legger en elektromagnetisk modell til grunn. Varmen er ifølge en slik modell elektromagnetiske bølger som da kan absorberes av og imiteres fra elektroner. Et elektron som absorberer energi fra en bølge vil da få energien fra en bestemt retning siden den aktuelle bølgen som avleverer den aktuelle energien har en retning. På den andre siden vet vi at en ladning som vibrerer og sender ut elektromagnetiske bølger vil sende ut disse bølgene i mange retninger (360° helt rundt). Om varmen i ulike stoff da består av slike  slik energiutveksling mellom ulike elektroner vil man alltid ha en spredning av varme, og det er da ikke mulig å reversere de aktuelle energioverføringene.

Absolutt temperatur, et bevis på at partikkelbevegelser?

 Vi kan vel ikke avslutte en historisk gjennomgang av varmens historie uten å nevne Lord Kelvin sitt bidrag som da har gjort at han har fått en temperaturskala oppkalt etter seg. Mange opplever det dessuten slik at det faktum at det finnes en minste temperatur, er et viktig argument for at partikkelmodellen. Her vil vi da si at det er allmenn enighet om at temperatur er bevegelser, men det er da ikke enighet om hva som beveger seg. Ifølge kinetisk partikkelmodell, så er det hele atomer/molekyler som beveger seg/vibrerer, mens andre mener at det i hovedsak er elektroner som beveger seg/vibrerer når .

Generelt kan man si at debatten om hva varme egentlig er, handler om det er mulig å bruke en ren mekanisk modell for å forstå alt som har med varme å gjøre. Er det med andre ord slik at den varmen vi til vanlig måler ved hjelp av et termometer, egentlig er en form for mekaniske bevegelser av partikler?  Eller er det heller snakk om et slags "kontinum" av energi som finnes mellom partiklene? Her vil vi bare kort nevne at man i de fleste praktiske beregningene behandler varmen som et slags kontinum som kan forflytte seg og som i denne sammenhengen kan utveksle mekanisk energi ved å forflytte stempler ol. Når noen ønsker å tro at all varme egentlig er mekaniske bevegelser i partikler så er det sannsynligvis  utfra et ønske om å forenkle det hele til å være et spørsmål om mekanikk som de da sannsynligvis opplever at de behersker.  

Som nevnt foran finnes det imidlertid endel observasjoner og argumenter som tyder på at mekaniske modeller ikke kan forklare alle sider ved varmen og alternative i denne sammenhngen er da ikke en gammel kalori-modell, men en elektromagnetisk modell. Ifølge en slik modell er det da snakk om ladninger som omgir seg med elektriske og magnetiske felt, og det er da i disse feltene man finner energien. Nå er det klart at ladninger kan vibrere eller oscillere  og dette innebærer i seg selv en form for mekanisk energi, men det er da også mulig å se på denne energien som en lagring av energi i elektriske og magnetiske felt. Fordelen med det siste er da at man også kan tenke seg at disse elektriske og magnetiske feltene kan løsrive seg fra ladningene i form av elektromagnetiske bølger og den totale energien i et stoff vil da bestå av elektriske og magnetiske felt som befinner seg mellom partiklene. Det betyr f.eks.at det ikke er nødvendig å postulere hastigheter på 1800km/h i gassmolekyler i vanlig luft for å kunne forklare hvor varmen i luften befinner seg. Problemet er bare at de som tror på den mekaniske varmemodellen tilsynelatende nekter å vurdere andre modeller, og derfor er det også få som er klar over at det finnes andre måter å forklare varme på enn den som finnes i vanlige lærebøkene.