


Lyd og bølger
15.10.03 Erling Skaar
Innhold:
1
Lys og lyd er bølger
2
Hva er lyd?
3 Frekvens og lydstyrke
4 Sentrale bølgebegrep
5 Hvordan fremstille bølger?
6 Lovmessigheter som gjelder alle
bølger
7 Bølgedemonstrasjoner
8 Lyd og musikk
9 Måleinstrument
Aktiviteter
Lysbølger,
lydbølger, og vannbølger forteller at vannkrana lekker - men hva er
felles for disse tre bølgene - og hva skiller dem?
Lys, lyd og vannbølger har endel fellestrekk. Derfor har vi her valgt å
behandle disse i sammenheng. Kunnskap om et av disse fagfeltene har overføringsverdi
til de andre. Det sentrale i alle disse fagfeltene er begrepet bølge
og forståelse for bølgebegrepet vil her være et hovedmål. Figuren til høyre
antyder at det er tre måter vi kan få informasjon om en kran som lekker, gjennom
øynene, gjennom ørene og ved at fingrene føler bølger i vannet. I alle tilfellene
er det snakk om en energioverføring via bølger.
Lyd er opprinnelig definert som det som øret kan høre.
Senere er lydbegrepet utvidet til å gjelde også svingninger med
høyere frekvens enn de øret kan høre (ultralyd)
og lyd med lavere frekvens (infralyd).
Lyd er energi
Generelt kan vi si at lyd er en form for energi som
forflytter seg gjennom ulike stoff (luft, vann og andre stoff) fra en sender
(stemmebåndet, høytaler ol.) til en mottaker (øre, mikrofon
ol). Se Animasjon .
Lyd er bølger
Lyd er en form for bevegelse (noe dynamisk) som sprer seg som bølger
og derfor sier vi at lyd er bølger. I praksis er det bevegelser eller vibrasjoner som sprer seg utover
fra lydkilden. Det er
altså ikke stoff som forflytter seg lydkilden til øret, men en bevegelse
i dette stoffet eller mediet som forflytter seg. Lydbølger
oppstår når noe vibrerer/svinger/oscillerer/dirrer (ulike
ord for det samme) og det som treffes av lydbølger vil begynne å
vibrere i takt med vibrasjonene i bølgen.
En bølge trenger et medium å bevege seg gjennom. Eksempler på slike medier
er luft, vann eller faste stoff. Lyd kan ikke bevege seg gjennom vakuum.
Siden bølger vanligvis vi spre seg over større og større områder etter hvert
som de beveger seg bort fra bølgekilden, vil lydstyrken avta etterhvert som
lyden fjerner seg fra lydkilden.
Alle bølger forflytter seg utover fra en bølgekilde og derfor vil en bølge
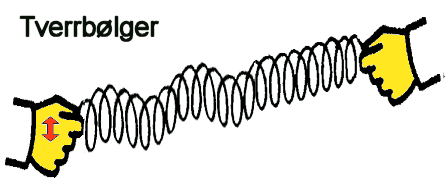
alltid ha en retning. Når det gjelder vannbølger vil disse bevege seg horisontalt
langs vannflaten, mens selve svingningene i mediet er da opp/ned. Svingningene
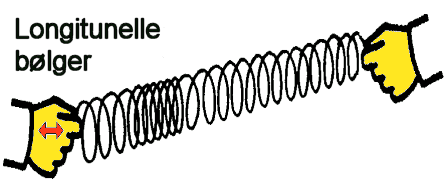
i mediet er altså på tvers av fartsretningen og derfor kalles bølgen for tverrbølger.
Lydbølger kalles derimot longitunelle bølger fordi de lokale svingningene
i mediet har samme retning som fartsretningen til bølgen. I praksis er det snakk
om fortetning (trykkøkning) og fortynning (trykkfall) av luften og alle bevegelsene
i denne sammenhengen vil da skje i den retningen som lyden beveger seg. (illustrert i figurer og i Animasjon )
Tverrbølgedemonstrasjon
En måte å "synliggjøre" bølger er å holde et 'Trappetroll' (= fjær som kan "gå" ned trapper) mellom hendene og så gjøre raske bevegelser med den ene hånden.
Hvis man beveger den ene hånden opp/ned vil man få tverrbølger som beveger seg
over mot den andre hånden.
Demonstrasjon
av longitunelle bølger
Om man i stedet beveger den ene hånden fram og
tilbake vil man få longitunelle bølger. Man vi da se at det blir en forflytning av en fortetning eller fortynning som beveger seg langs fjøra over til den andre hånda. Det er da noe tilsvarende som skjer i luft og andre steder hvor luft brer seg.
Forslag til korte beskrivelser av hva lyd er:
*Lyd i luft er raske fortetninger og fortynninger av luft som brer seg utover
fra lydkilden
*Lyd er molekylbevegelser/atombevegelser som forplanter seg bort fra lydkilden.
*Noen sier at lyd er svingninger. Dette er uheldig. Bedre: Lyd er svingninger
som forplanter seg utover fra lydkilden (Merk at mange barn tenker på en form for dreiing når de hører ordet svingning.
Denne koblingen bør vi kanskje prøve å "luke vekk".)
Bølget hår og bølgeblikk er ikke ekte bølger fordi de ikke er dynamiske. De har bare en form som likner.
Bølger er noe dynamisk
- ikke statisk
Bølge er et viktig begrep både i fysikk og i dagliglivet. De fleste vil vel ikke ha noe problem med dette begrepet i dagliglivet. Det er vel
vanligst bruke det i forbindelse med vann (vannbølger). Grunnbetydningen
av begrepet bølge er noe dynamisk (noe som beveger seg), men bølge kan også brukes om statisk ting som bølgeblikk og bølger i håret. De assosiasjonene som ordet bølge gir er avhengig av situasjonen ordet brukes i. Finn gjerne flere eksempler hvor det er vanlig å bruke ordet bølge.
Årsak til bølger
I fysikksammenheng er vi vanligvis på jakt
etter karakteristiske kjennetegn på ulike fenomen og i mange sammenhenger er
disse karakteregenskapene mer viktig enn selve fenomenet. Det betyr i denne
sammenhengen at det er bestemte egenskaper ved bølgen som er det sentrale og ikke den fysiske utformingen av bølgen. Siden det er vanskelig å tegne bølger er det vanskelig å danne seg et visuelt bilde av en bølgebevegelse. Dette er nok en viktig årsak til at bølgebegrepet i fysikken erfaringsmessig
er vanskelig å forstå. En måte å forenkle presentasonen av bølgebegrepet er
å først konsentrere seg litt om hva som er årsaken til bølger. Her vil vi da
si at det er svingninger eller
vibrasjoner som er årsaken til bølger.
"La det svinge"
Generelt
er det lettere å studere svingninger enn bølger. Ganske mye i omgivelsene våre vil svinge om
vi påvirker det med krefter.
Med svingning mener vi da her en fram- og
tilbakebevegelse som gjentaes noen ganger. En linjal som henger i hullet vil
svinge. Dette er da et eksempel på en svingning som ikke gir lyd fordi svingehastigheten
eller frekvensen er for liten. Hvis vi derimot holder en linjal fast til en bordflate kan
vi få svingninger som er så raske at vi får en hørbar
tone.
På animasjonen til venstre har vi markert luften med en gulfarge og denne
luften vi vekselvis presses sammen og utvides og det er da disse endringene
i lufttrykk som vil spre seg utover som lydbølger.
Tenkeoppgave: Nevn andre eksempler på at ting svinger. Hva er det som
bestemmer hvor fort linjalen eller tilsvarende gjenstander vil svinge?
Litt om lydhastighet
Lyd vil ha ulike hastigheter i ulike medier. Lyd vil vanligvis gå fortere jo stivere mediet er. Videre vil det gå seinere jo tyngre et medium er. Det betyr f. eks. at lyd som
en hovedregel vil gå fortere i faste stoff enn i væsker (faste stoff
er stivere enn væsker) og fortere i aluminium enn i bly (fordi bly er tyngst/har
størst massetetthet). Tabellen under viser lydhastigheten i noen stoff.
Lydfart i noen stoff:
|
|
Luft (20°
C): 0,34 km/s
|
|
Bly: 1,2 km/s
|
|
Hydrogen: 1,3 km/s
|
|
Vann: 1,5 km/s
|
|
Kopper: 3,7 km/s
|
|
Granitt: 4,0 km/s
|
|
Stål: 5,0 km/s
|
|
Aluminium: 5,1 km/s
|
|
Om vi f.eks. har en lang fritthengende ståltråd er det mulig å høre at lyden fra et slag på tråden i den ene enden går fortere til den andre enden gjennom tråden enn gjennom luften. Lyden
trenger ellers ca 3 sekund for å gå 1 km gjennom luft. Denne huskeregelen
kan da være utgangspunkt for å bestemme avstanden til et lyn eller avstanden til en eksplosjon. Man tar da tiden fra man ser at ting skjer (lynblink eller annet) og så måler
man tiden til man hører lyden.
3a
Frekvens
|
Frekvens er definert som antall svingninger pr sekund.
(Med
matematiske symbol: f = #/t)
|
Et annet ord for frekvens i forbindelse med lyd er tone og vi snakker
da om lys tone når frekvensen er høy og mørk tone
når frekvensen er lav
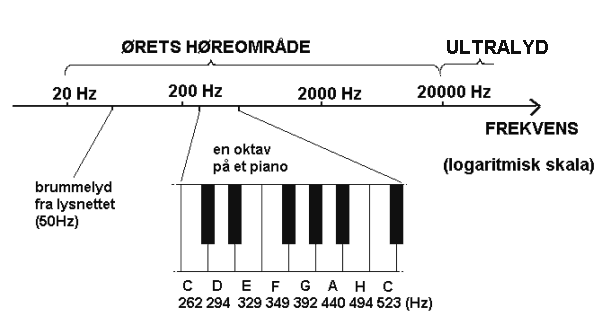
Menneskeøret kan høre frekvenser/toner mellom ca 20Hz og 20kHz. Eldre mennesker vil
vanligvis ikke høre de lyseste tonene. Hunder kan på den andre
siden høre lyder med
frekvens omkring 30kHz ( hundefløyte) og flaggermus bruker lyder opp mot 40kHz når de orienterer seg i mørket. Slike
lyder men frekvens over det menneskeøret kan høre kalles ultralyd.
Ulike frekvenser kan demonstreres ved hjelp av en tonegenerator
Det kan enten være en egen enhet med ulike brytere høytaler (se
figur), eller
så kan det være et program i en datamaskin. De fleste nyere datamaskiner har
innebygget lydkort og tilkoblet høytalere. Fordelen med å bruke datamaskinen
til å demonstrere ulike lyder er at vi da vanligvis kan "se" lyden
på skjermen samtidig som vi hører den.
3b Lydstyrke
En lyd kan
være sterk eller svak.
|
Lydstyrke
kan måles med lydnivåmåler / støymåler
/ desibelmåler og vanlig benevning er desibel (dB)
|
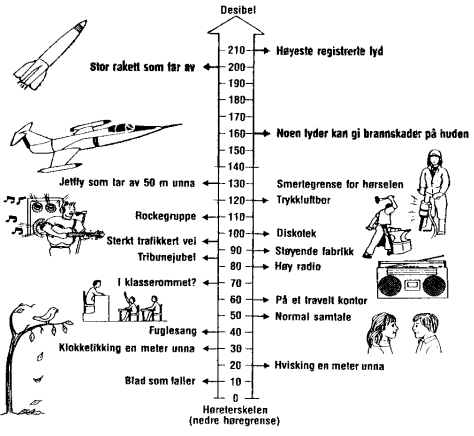
Figuren
til høyre er hentet fra ei lærebok og viser noen typiske lydstyrkeverdier.
Energi i lyd:
Merk at dB-skalaen er logaritmisk og en dobling av energien
i lyden svarer til en
økning på ca 3 dB.
Merk videre at lyd og andre energiformer som sprees fra en kilde normalt
vil avta som 1/d² hvor de er avstanden til lydkilden. Det betyr i praksis at
en dobling av avstanden fra lydkilden vil bety en reduksjon av lydstyken til
en firedel. Det svarer da til to halveringer eller en reduksjon på 6 desibel.
En matematisk definisjon av desibel:
Lydnivå (intensitet) til en lyd
med intensitet I i desibel b er
definert :
b = 10· log(I /
I0)
hvor I0 er en
referanseintensitet som er antatt å være ørets høregrense
(10-12W/m2)
Oppfatning av lyd:
Merk at desibel er ment å fortelle noe om hvordan
øret oppfatter lyd og det er vanskelig å si noe sikkert om dette. Ulike mennesker
vil gjerne ha ulike meninger om hva en dobling av lydstyrke vil innebære. Her
følger noen sitat om lydstyrke og disse viser vel at man kan være uenige om
hva som oppfattes som en dobbling av lydstyrke. I det første sitatet sier man
at en dobling svarer til 10 dB mens det andre sitatet sier at det svarer til
6 dB. Merk at det siste sitatet handler om energien i lyden og om man utfra
disse sitatene ønsker å trekke ut en enkel huskeregel, så kan
man kanskje si at en endring på 10dB svarer til 10 i energiforskjell og
2 i høreforskjell.
Lydstyrke måles i desibel (dB). En økning av lydnivået på 10 desibel
oppfattes som en fordobling. Stille skog har en lydstyrke på litt under 20 dB.
Måleenhet for
lydstyrke. Symbolet for desibel er dB(A). Måleenheten er en logaritmisk skala.
En økning på 6 dB(A) oppfattes som en fordobling av menneskeøret. For å ta
hensyn til hvordan mennesker oppfatter ulike frekvenser i lyden, benyttes
forskjellige filtre, eller veiekurver, ved støymålinger. Den vanligste
veiekurven benevnes med bokstaven A (dBA) (http://miljo.mip.no/ord.htm)
desibel dB - målenhet for lydstyrke, angir hvor mye energi som
blir overført med lyden. En økning på 10 dB, f.eks. fra 70 til 80 dB, tilsvarer
en ti ganger så høy lydstyrke.
Merk at en forskjell på 20dB svarer til 100 i energiforskjell (10*10=100
og ikke 10+10=20). Dette svarer da til 4 i høreforskjell (2*2=4 og ikke 2+2=4
selv om de gir samme tall i dette tilfellet)
I dagligtale bruker vi begrepene høy/lav om både lydstyrke og tone
og det kan gi uheldige misforståelser. Hva menes f.eks. med en høy lyd? Er det
frekvensen som er høy eller er det lydstyrken som er høy? Her vil vi derfor anbefale å
bruke begrepene lys/mørk og sterk/svak for å karakterisere lyd
og ikke høy/lav.
Ørets høreområde
Det er videre
nyttig å studere grafiske kurver som viser sammenhengen mellom frekvens
og lydstyrke. Det er viktig at elever får en klar forståelse for forskjellen mellom lydstyrke og tonehøyde.
En måte å klargjøre denne forskjellen på er å bruke
grafiske fremstillinger som viser frekvens langs x-aksen og
lydstyrke langs y-aksen. I et slikt skjema vil det totale lydbildet
fremkomme som en kurve.
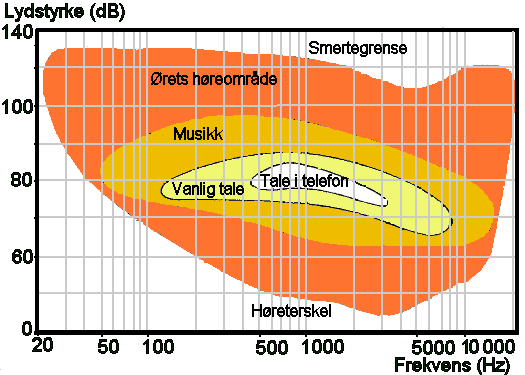
Figuren til høyre viser øvre og nedre grenser for både
frekvens og lydstyrke i ulike vanlige lyder samt høregrense (nederst)
og smertegrense (øverst) for det menneskelige øret. (fra en læreboka Livsstil og helse for 7-9 klasse
)
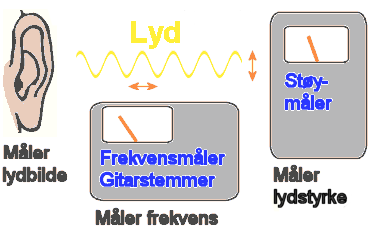
Hørsel og stemmeorgan
Hovedårsaken til at vi er interessert i lyd er at vi mennesker har
ører som kan oppfatte lyd. Ørene er da i prinsippet en lydmåler,
som kan skille mellom lyse og mørke toner og sterke og svake lyder. Ørets
primære oppgave er imidlertid å tolke lydbilder og derfor er det
mindre egnet til å bestemme frekensverdier og desibelverdier. På
den andre siden har vi stemmeorganene som kan lage svært mange ulike lyder,
men kanskje ikke så harmoniske som de vi får fra en tonegenerator.
I denne sammenhengen er det viktig å være klar over at stemmeorganene
våre og hørselorganene våre er svært avanserte fordi
de er skapt for å formidle ulike typer informasjon. De instrumentene vi
bruker for å måle lyd er egentlig mye mer primitive og kan i prinsippet
bare plukke ut to faktorer, nemlig frekvens og lydstyrke. I forbindelse med
hørselskade er lydstyrke den sentrale faktoren siden sterk og vedvarende lyd kan ødelegge hørselen. På
den andre siden er det vel frekvensen som er viktigst å bestemme i forbindelse
med musikk, siden musikalske mennesker kan være svært var for "falske
toner".
Bølge er et sammensatt begrep, fysisk sett. Forståelse for bølgebegrepet forutsetter altså forståelse for endel andre mer grunnleggende begrep. Her følger de viktigste begrepene som brukes i forbindelse med bølger:
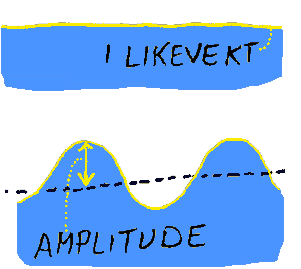
Likevektstilstand I fysikken er bølger alltid svingninger, utslag eller bevegelser omkring en såkalt likevektstilstand. Likevektstilstanden er da den tilstanden hvor det mediet som svinger kan være i ro.
Amplitude/utslag/styrke/intensitet er da størrelse på utsvinget fra likevektstilstanden. Dette er ofte en lengde-enhet (i vannbølger, gitarstreng, pendel ol.). I lydbølger har vi trykkendring og i lysbølger dreier det seg om elektrisk (og
magnetiske) feltstyrke som står normalt på fartsretningen. I dette heftet bruker vi amplitude som et generelt begrep som er uavhengig av hva slags bølge vi har med å gjøre. Benevningen
for amplituden vil være forskjellig avhengig av hva slags bølge
det er snakk om. Merk at dette begrepet forutsetter et visst abstraksjonsnivå hos elevene, og om læreren oppdager at elevene har problemer med å forstå det abstrakte begrepet amplitude, så kan man
bruke begrep som styrke (lydstyrke/lysstyrke) eller intensitet som da uttrykk for det samme.
Om vi bare bruker ordet intensitet, så vil vel kanskje noen elever få problemer med å se sammenhengen mellom dette ordet og de bølgene som er tegnet i boka eller på tavla. Generelt kan det vel være nyttig å bruke flere ord, og på den måten "presse" elevene til å se det som er felles i alle ordene ovenfor.
Svingetid er tida mellom hver gang mediet (pendel, vann, luft, eter..) er i en bestemt svingetilstand. Det vil f. eks. si tiden mellom hver gang mediet passerer likevektstilstanden i en av retningene. Det er også tiden mellom når to etterfølgende
"bølgetopper" eller "bølgebunner" passerer et punkt. Symbolet for svingetiden er T (stor bokstav) og enheten er s (sekund).
Frekvens er antall svingninger pr tidsenhet (definisjon). Vi får standardbenevningen for frekvens når vi bruker 1 sekund i definisjonen. Symbolet for frekvens er f og enheten er Hz. (Hz(hertz)
= #/s (=antall/sekund))
De begrepene som er nevnt her gjelder både for svingninger og bølger. Forskjellen på svingninger og bølger er primært at bølgene forflytter seg i rommet. Svingningene vil derimot "står i
ro". Det vil si at de svinger fram og tilbake om et punkt i rommet. Når en bølge forflytter seg i rommet, er det ikke selve mediet som forflytter seg, men en bestemt bevegelse av mediet. På grunn av denne forflytningen i rommet har vi for bølger to ekstra begrep:
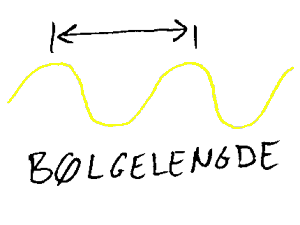
Bølgelengde er avstanden (alltid lengdeenhet) langs med fartsretningen fra f.eks. en bølgetopp til neste. Symbol er l (lamda) og enheten er m (meter). Det er lett å peke på bølgelengden når vi har tegnet en bølge.
Bølgefart/bølgehastighet er hastigheten som f.eks. en bølgetopp beveger seg med langs med fartsretningen. Symbolet er v (c for lyshastigheten i vakuum) og enheten er m/s.
Formler: Når det gjelder bølger er der to formler som er nyttige i ulike sammenhenger. Disse er:
Frekvens er antall svingninger pr sekund
f=1/T (frekvens=1/svingetid) [Hz=1/s]
|
|
Bølgehastighet er hastigheten som bølgen beveger seg
v=l/T (bølgehastighet=bølgelengde/svingetid) [m/s=m/s]
|
Disse er en direkte følge av definisjonene av de enkelte størrelsene og de vil derfor alltid gjelde. Merk at f=1/T er formelen som gir frekvensen til en svingning/bølge, mens Hz=#/s er tilhørende benevninger. Ved å studere en fremstilling av en bølge, kan vi relativt lett overbevise oss selv om at formlene må være rett. Når vi lurer på om vi har husket formlene rett, er det da nyttig å sjekke om benevningene stemmer. Om vi kombinerer formlene ovenfor får vi f.eks. v=lf som vi ofte kan se i ulike bøker. Det er da disse begrepene som vi vanligvis hører om, og derfor er
det også aktuelt å pugge denne formelen, hvis vi da ikke satser på å utlede den fra "definisjonsformlene" ovenfor.
Tidsmessige endringer er vanskelig å fremstille på et ark
Svingninger og bølger er noe som skjer over tid, og derfor er det vanskelig å fremstille dem på et ark. Film som kan gjengi bevegelser over tid, er ofte bruk for å vise bølger. Det er imidlertid ikke så mange skoler som har prioritert slikt utstyr.
Etter at datamaskiner ble vanlig i skoler er det mulig å bruke enkle gif-animasjoner
av den typen som er vist ovenfor. Men om man virkelig skal forstå de ulike sidene
ved bølger, er det viktig at man er aktiv selv, og i denne sammenhengen er det
aktuele å bruke vanlig papir og tavle. I den virkelige verden er det mye som kan distrahere oppmerksomheten bort fra det sentrale. Om vi f.eks. bruker vann kan det være at barna blir mer opptatt av vannsøl eller spesielle optiske effekter enn det karakteristiske ved bølgene. I fysikkundervisningen er det vanlig å bruke skisser og figurer for å beskrive visse fenomen framfor å se
på virkeligheten direkte. På et blankt papir kan vi da bare tegne det vi ønsker
oppmerksomhet om. Vi kan altså "klippe vekk" uvesentlige ting og "fryse" bevegelser.
Her følger noen enkle eksempler på hvordan vi kan tegne svingninger og bølger:
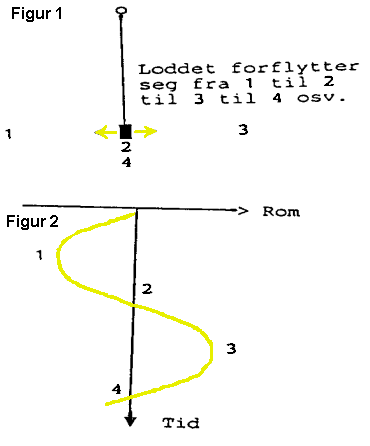
1
Svingninger på et ark Et ark har den begrensningen at det består av to dimensjoner. Om vi ser på svingningene til en
pendel, er utslag fra likevekt og tid de sentrale variablene. Man kan derfor fremstille svingningene i et rom-tid-diagram. Dette er vist til venstre
(figur 2). Noen vil kanskje ha vansker med å se sammenhengen mellom en slik
kurve og den virkelige situasjonen. En forutsetning for å forstå slike kurver
er at vi forstår hva det innebærer at tiden er lagt ned i en av aksene. Den enkleste måten å "tegne" pendelsvingninger er vel å tegne pendelbanen i to dimensjoner (figur 1). Problemet
med denne tegnemåten er at vi da må forklare at pendelen først er ved
1, så ved 2 , så ved 3 osv. Det er med andre ord endel ting som vi ikke får
"overført til arket". Hovedproblemet med denne måten er kanskje at vi ikke "ser" tidens betydning. Pendelsvingninger er en funksjon av tiden, og dette kommer tydeligst fram i rom-tid-diagrammet (figur 2). Her har vi altså valgt ut en romdimensjon og lagt den langs x-aksen. Så har vi tilføyet tidsdimensjonen og lagt den til y-aksen. Dette
viser da at vi får en sinuskurve eller bølgeform som resultat.. Merk at dette
ikke er en virkelig bølge fordi den ikke endres over tid.
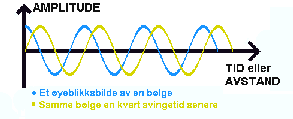
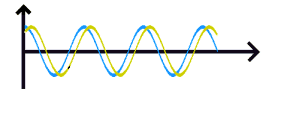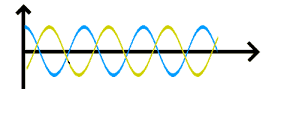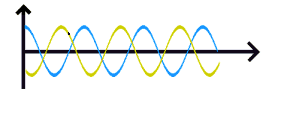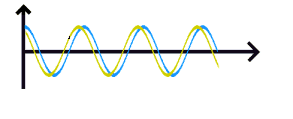
2
Bølger på et ark Bølger er vanskeligere å fremstille grafisk. Foruten tida har vi utslaget og fartsretningen som også bør ha hver sin dimensjon på arket. Det er
da vanskelig å tegne tre dimennsjoner på et todimensjonalt ark. Til vanlig
er det da tida som må vike. Vi fremstiller med andre ord et øyeblikksbilde av bølga med f.eks. utslaget langs y-aksen og fartsretningen langs x-aksen. På samme figuren kan vi da tegne hvordan bølgen vil se ut f.eks. 1/4 svingetid seinere med en annen farge. Noen
vil vel ha problemer med å forstå dynamikken i bølgebevegelsen utfra slike "still-bilder". Fordelen med å fremstille bølger og svingninger på papir, er at vi lett kan "peke på" hva som menes med begrepene bølgelengde,
bølgefart, frekvens svingetid osv. Fremstillingene kan også være til hjelp når vi skal forklare og begrunne de to formlene som følger.
Figuren over til høyre er gjort interaktiv og om man plasserer muspekeren over
den vil man se en animasjon av bølgen. Det innebærer da at figuren automatisk
vil endre seg med tiden. Her har vi da valgt å la den blå kurven som representerer
et øyeblikksbilde av bølgen bestå slik at man kan se forskjellen på et øyeblikksbilde
av en bølge og en bølge som beveger seg. Merk ellers at det aktuelle mediet
som bølgen går gjennom vil bevege seg opp og ned - ikke mot høyre slik figuren
kanskje gir inntrykk av. Dette er understreket ved at det svarte merket
på animasjonen.
Ulike måter å tegne en bølge
I skoleverket er
vi er det snakk om tre typer bølger. Disse er vannbølger, lys og lyd, men det
er ikke alltid opplagt at det er snakk om bølger. Det har da sammenheng med
at man tegner disse bølgefenomene på ulike måter. Her vil vi nevne tre prinsipielt ulike måter å tegne bølger på. Vi kan med andre ord tegne en lysbølge på tre ulike måter. Sammenhengen bestemmer da hvilke måte vi velger. I praksis er det ofte en av disse metodene som utmerker seg framfor andre i konkrete situasjoner. Her vil vi kort kommenterer fordeler og ulemper med de ulike metodene.
Tegnemetode 1: "Fra siden". Nå er uttrykket "fra siden" hentet fra vannbølger. Vi vil ikke "se" det karakteristiske bølgemønsteret når vi ser lysbølger og lydbølger fra siden.
Vi tegner likevel de karakteristiske bølgestrekene også når vi snakker om lys og lyd. Bølgemønsteret i disse tilfellene henspeiler da på henholdsvis en endring i feltstyrke eller tetthet av luft. Her vil vi ikke gå nærmere inn på dette, men bare konkludere med at
vi her kaller de sinusformede tegningene av bølger for "fra siden"-tegning. Vi bruker denne tegnemetoden når vi ønsker å få fram prinsippene for alle typer bølger.
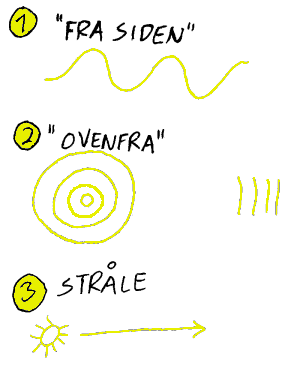
Tegnemetode 2: "Ovenfra". Når vi ser vannbølger ovenfra vil vi ofte se ringer (bølgefronter) som beveger seg utover fra det som skaper bølgene. Generelt kan vi si at vi ser ringer om vi befinner oss nær bølgekilden og har et stort overblikk. Om vi derimot befinner oss langt fra bølgekilden og dessuten har et begrenset overblikk, vil bølgene se ut som parallelle rette bølgetopper som beveger seg i en retning. Denne tegnemetoden er spesielt nyttig når vi vil få fram årsaken til interferens (periodevis utslukking og forsterkning av intensitet) i lys eller lyd. Interferens oppstår når to "samstemte" kilder (spalter eller to høytalere med monosignal) sender ut bølger som møter hverandre. Denne tegnemetoden er nyttig for alle typer bølger om vi vil skaffe oss et generelt overblikk over hvordan bølger beveger seg og hvordan de vekslevirker.
Tegnemetode 3: "Stråle". Om bølgelengden er liten i forhold til vårt synsfelt (stort overblikk), vil vi oppleve at bølger går rett fram. Vi vil da få "skygger" som har en tilnærmet rett kant når bølgene møter noe de ikke kan trenge gjennom. Når det gjelder vannbølger og lydbølger er det sjeldent at vi tegner disse som stråler. Grunnen er at de har relativ stor bølgelengde og derfor vil de bli avbøyet rundt hindringer i stedet for å lage klare
"skygger". Når det derimot gjelder optikk ol, er det vanlig å tegne lys som stråler. En stråle er da en strek som går fra lyskilden til der lyset ender. Merk at når vi tegner lys som stråler, så har vi "mistet" bølge-egenskapen som er den egenskapen som egentlig kan forklare brytning og refleksjon. Når vi tegner lys som stråler ønsker vi imidlertid å få fram hvor lyset beveger seg og ikke hvorfor det beveger seg slik vi har tegnet.
Det som er nevnt hittil gjelder generelt for alle typer bølger. Noen
forklaringer er relativt avanserte og det er ikke sikkert at disse bør inn i pensum i grunnskolen.
Det er imidlertid viktig at lærerene vet mer enn elevene om det han skal undervise om.

Derfor er disse
forklaringene med. Vi skal nå gå over til å se på noen egenskaper for bølger som gjelder mer eller mindre for alle bølgetyper. Disse egenskapene er da beskrevet på en slik måte at det kan være aktuelt å presentere disse i grunnskolen. I lærebøker er det vanlig å ta utgangspunkt i konkrete eksempler og så formulere lovmessigheter ut fra det som vi kan observere. Her vil vi formulere lovmessighetene først og så senere se på eksempler og
aktiviteter. Lærerens oppgave er ofte
å lære elevene en eller annen lovmessighet. Hvis læreboka bare har ett eksempel kan det være i minste laget for enkelte elever. En lærer med en "dypere" forståelse for de ulike bølgefenomenen vil da lett kunne nevne opp flere eksempler hvor denne lovmessigheten gjelder og slik hjelpe elevene til å oppdage det som er felles for alle eksemplene. Jo flere eksempler jo lettere er det vanligvis for elevene å oppdage lovmessigheten. Læreren skal med andre ord prøve å finne eksempler utfra lovmessigheter. Elevene skal bygge opp en forståelse av lovmessigheter utfra eksempler. Her vil vi da først nevne lovmessighetene og gi eksempler fra vannbølger, og så vil vi komme tilbake til lyd og lys senere.

1 En bølge kan ha ulike hastigheter i ulike medier. Frekvensen eller svingetiden vil alltid være den samme
(frekvensen vil ikke endres over tid når vi ser på ei bølge). Om ikke dette gjaldt, kunne vi få opphopning av bølger der hvor ei bølge skifter hastighet. Det er "unaturlig". Det betyr ifølge formelen v=lf at bølgelengden må bli kortere når hastigheten blir mindre. Dette kan observeres når vannbølger går fra et dypt område til et grunt område. Hastigheten til bølgen er mindre på det grunne området og bølgelengden blir da også mindre.
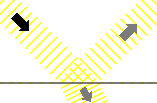
2 En bølge reflekteres vanligvis når den treffer et annet medium. Refleksjonsvinkelen vil da være lik innfallsvinkelen. Se figur. Dette kan vi observere når vannbølger slår mot en bergvegg eller en mur. På ei strand blir bølgene så mye dempet eller absorbert at det er vanskelig å observere noe refleksjon.
Lyd reflekteres vanligvis når den treffer et annet medium.
Når det gjelder lyd er ekko et kjent fenomen. Vi
kan f.eks. høre at lyden fra bilhjulene blir reflektert fra autovern og murvegger slik at vi kan høre når vi kjører forbi slike. Enkelt kan vi få demonstrert dette ved å holde håndflata litt fra kinnet og si noe. Lyden vil da bli reflektert fra håndflata til øret. Glatte overflater reflekterer mer lyd enn en ru overflate med mange hull. Dette er grunnen til at tak i klasserom og andre offentlige rom vanligvis har en ujevn overflate. Slike
overflater demper lyden i stedet for å reflektere lyden.
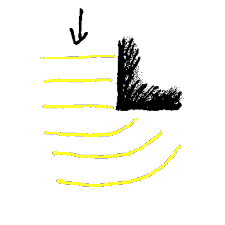
3 Ei bølge kan "gå rundt hjørner". I vann kan vi observere at bølgene har en tendens til å bøye av bak en holme eller liknende. Bak et smalt sunn sprer den seg ut til hver side.
Lyd kan "gå rundt hjørner". Alle har vel erfart at vi kan høre
ting bak hjørner ol. før vi ser det. Lyden går da rundt hjørner, selvom
den også i noen tilfeller kan reflekteres fra husvegger ol. Det at lyd bøyes er en typisk bølgeegenskap. Merk at det er de dype lydene (de som har lavest frekvens) som blir mest avbøyet. Disse er da lettest å høre rundt hjørner. Det er dette som gjør at vi ofte hører stortromma i et korps før skarptrommer og musikken. I hus er det vanskeligst å isolere for basstonene fra et stereoanlegg. Dette har sammenheng med at veggene lettest "svinger med" de dype tonene og følgelig går disse lettere gjennom veggen.


4 Ei bølge vil avbøyes når den går på skrå mellom to medier som har ulik bølgehastighet (brytning/refraksjon). En slik avbøyning kan vi observere når vannbølger går mellom områder med ulik dybde. Om vi tegner bølgetoppene som parallelle streker, vet vi at bølgene beveger seg normalt i forhold til strekene. Hvis vi så skal få streker med to ulike avstander (bølger med to ulike bølgelengder) til å henge sammen, viser figuren til venstre at bevegelsesretningen til bølgen må endres. Andre alternativ medfører "opphoping av" eller "mangel på" bølgetopper
som da er umulig.

5 Bølgelengden er en begrensende faktor for oppløsning.
Med oppløsning mener vi her evnen til å skjelne detaljer fra hverandre utfra den informasjonen vi får fra bølger. Dette begrepet gjelder særlig for lys og lyd som vi har sanseapparat for å oppfange
retning til ulike bølgekilder. Det er derfor lite aktuelt å snakke om oppløsning i vannbølger. Figuren
til høgre illustrerer da at gjenstander som har en størrelse omtrent lik
bølgelengden ikke vil lage skygge. Det har da sammenheng med at bølgene vil
bøyes litt innover nær alle gjenstander de passerer.
Bølgelengden er en begrensende faktor når det gjelder å bestemme retning
til en lydkilde. Regelen er da at det er lettere å bestemme retningen til lydkilder med høye toner (høy frekvens) enn lave toner (lav frekvens). Et forsøk som illustrerer dette får vi om en elev får bind for øynene og så skal peke på ulike lydkilder. Det
vil da være vanskeligere å bestemme retningen til en basstone i forhold til
en diskanttone. Småfugler bruker høye frekvenser og det er da vanligvis lett
å høre hvor de er. Flaggermusene sender ut ultralyd (lyd med frekvens som er høyere enn det vi kan høre). Når disse lydene blir reflektert kan flaggermusen "se" det som reflekterte lyden med forholdsvis stor oppløsning.
Merk ellers at vi trenger to ører for å bestemme retning. Prinsippet
er da at lyden når de to ørene på litt forskjellige tidspunkt
og denne tidsforskjellen vil hjernen vår tolke som at lyden kommer fra
en bestemt retning.
6 Egenfrekvensen bestemmer hvilke bølger som påvirker stoffet. Alt vi har rundt oss og i oss kan svinge/vibrere. Hver gjenstand/ting har da en eller flere svingefrekvenser som de foretrekker. En slik frekvens kalles egenfrekvens. Blir så et medium utsatt for bølger med frekvens som er lik egenfrekvensen kan mediet få sterke svingninger. Dette kalles resonans. Dette utnyttes særlig i musikkinstrument. Også bølgekraftverk og laser utnytter tilsvarende effekter. Da Tacoma Bridge i USA raste sammen i si tid, var det fordi vinden satte den i svingninger. Disse ble til slutt for store. Et annet eksempel på resonans er en gitarstreng som begynner å svinge sammen med lyden i rommet. Når et glass sprekker fordi noen synger bestemte toner så skyldes det at sangeren har truffet på en av egenfrekvensene til glasset.
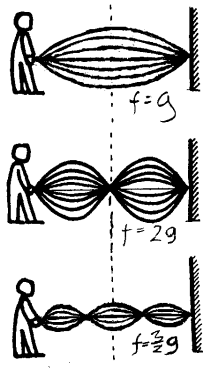
Stående
bølger
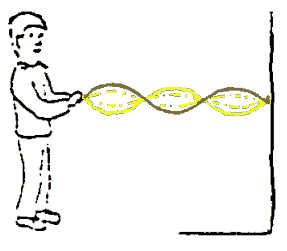
En bølgedemonstrasjon
Et enkelt demonstrasjonsforsøk er å bruke en lang horisontal stålfjær som er festet i begge endene. Slike kan kjøpes fra læremiddelfirma. På en slik fjær vil vi kunne "peke på" likevektstilstanden
(fjær uten bevegelser i), amplituden (avstanden fra likevektposisjon til
maksimalt utslag), svingetiden (tid for en fram og tilbakesvingning), frekvensen, bølgelengden
(avstanden mellom to bølgetopper) og bølgefarten (farten til en
bølgetopp). Slike demonstrasjoner er viktige for å forstå innholdet i de aktuelle
begrepene. Merk også at det er mulig å vise både bølger og svingninger (ofte kalt stående bølger) ved hjelp av en slik fjær. Stående bølger er da resultatet av at utsendte bølger møter reflekterte bølger og resultatet blir da at noen punkter på fjæra svinger mye mens andre punkter vil bevege seg svært lite.
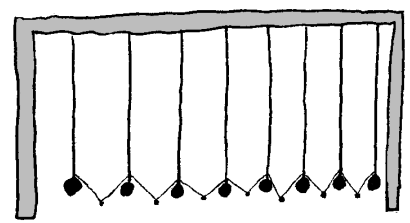
Koblede
pendler
Koblede
pendler
En annen måte å synliggjøre denne typen longitunelle bølger er ved hjelp av såkalte koblede pendler. Hvis vi mellom mange like pendler henger en hyssingbit med et lite lodd vil vi kunne observere at pendelsvingninger i en pendel vil forplante seg videre fra pendel til pendel. Dette utstyret kan da illustrere både longitunelle bølger og tverrbølger avhengig av hvilke veg vi svinger den første pendelen.
Gode og dårlige modeller
I litteraturen finner man ulike modeller som har til hensikt å hjelpe oss til å forstå begrep som lufttrykk og lyd. Den såkalte partikkelmodellen (kinetisk partikkelmodell for gass) går da ut på at luft består av mange partikler (luftmolekyl) som beveger seg fritt i forhold til hverandre bortsett fra i de tilfelle de kolliderer med hverandre. Temperaturen forteller da noe om gjennomsnittshastigheten til luftmolekylene og ifølge denne modellen er gjennomsnittshastigheten til luftmolekylene ved 20°
C ca. 500 m/s (svært stor hastighet). Denne modellen kan da til en viss grad forklare lufttrykk mot vegger og annet som summen av mange kollisjoner. Men det er mye vanskeligere å danne seg et forståelig bilde av hvordan en lydbølge beveger seg gjennom luft om vi antar at luften består av svært små partikler som ikke påvirker hverandre bortsett fra når de av og til kolliderer. Når vi her nevner denne modellen så er hensikten bare å gjøre lærere oppmerksom på at mange mener at partikkelmodellen kan virke forvirrende om man skal prøve å forstå hvordan lyd beveger seg gjennom luft.
Alternativet til denne modellen er da en modell hvor man antar at luftmolekylene hele tiden "kjenner" frastøtende krefter fra nabomolekyl. Om så et nabomolekyl forflytter seg litt som følge av noe som vibrerer, så vil det da bli en ubalanse i kreftene slik at også det neste luftmolekylet vil flytte litt på seg. I faste stoff og væsker er det vanlig å anta at lyden sprer seg mellom atomene via krefter som virker mellom atomene. Man kan da bruke de koblede pendlene som er nevnt ovenfor for å danne seg et bilde av hvordan lyd sprer seg i f.eks. en tråd. Men er det da ikke også nærliggende å tro at dette også er tilfelle i luft? Forskjellen på væske og luft er primært
at kreftene mellom luftmolekylene er mye svakere fordi de befinner seg lenger fra hverandre. Her vil vi ikke gå nærmere inn i denne debatten, men bare konkludere med at partikkelmodellen er en modell som ikke er bevist. Når den fikk så bred plass i L97 som den fikk, så har det sannsynligvis sammenheng med at noen trodde at partikkelmodellen var mer grunnleggende og nyttig enn den virkelig er.
Se artikkel om partikkelmodellen
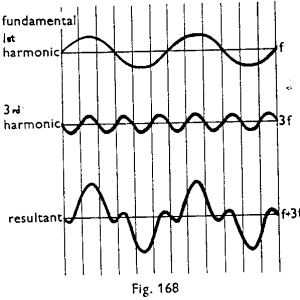
Musikkinstrument kjennetegnes av at de gir fra seg lyd med ulik toner eller frekvens, og nedenfor følger en vanlig toneskala hvor bokstavene er tonenavn og tallene viser tilhørende frekvenser.
262 294 329 349 392 440 494 523 (Hz)
C D E F G A H C (tonenavn)
Grunntone
og overtoner på en streng
Merk spesielt at samme tonenavn går igjen hver gang en frekvens dobbles. Det har sammenheng med at toner med dobbel og halv frekvens klinger godt sammen og i musikksammenheng høres de da ut som samme tone.
På en streng betyr det at forholdet mellom antall utbulinger er 1:2. I
eksemplet til høyre vil da den andre strengen gi en frekvens som er
dobbelt så stor som den første. Avstanden mellom en tone og en tone med dobbel frekvens kalles oktav. I en gitar har den tykkeste strengen navnet E og den har da en frekvens på 165 Hz som er halvdelen av tallet som er oppgitt ovenfor. Den tynneste strengen på en gitar er da også en E som har frekvens 658Hz. Det betyr at det er to oktaver mellom disse strengene. Nå
finnes det også andre frekvenser som klinger godt sammen og et eksempel
er frekvenser hvor forholdet er 2:3. Det svarer da til andre og tredje streng
på figuren til høyre. Om den andre strengen f.eks. gir tonen C,
vil da den tredje strengen gi tonen G som da hører med i C-dur akkorden.
En akkord i musikken er en samling toner som klinger godt sammen. Når
vi f.eks. spiller gitar, så slår vi vanligvis på flere toner
samtidig når vi f.eks. har en C-dur akkord er det tonene C, E og G som
klinger sammen.
Årsaken til at noen toner klinger bedre sammen enn andre har sammenheng
med at ulike musikkinstrument ikke gir bare en tonen, men en samling av flere
toner. Den tonen som har lavest frekvens kalles ofte grunntonen. Navnet henspeiler
på at det er den laveste tonen, og dessuten er det også oftest den
sterkeste tonen. Når vi slår på en gitarstreng får man i
tillegg såkalte overtoner som da f.eks. har dobbel frekvens eller andre frekvenser som klinger ok sammen med grunntonen. Når ulike musikkinstrument har forskjellig lyd selv om de gir samme toner så har dette sammenheng med at de ulike instrumentene gir ulike overtoner.
I strenginstrumenter er det 1) tykkelsen til strengen, 2) strammingen til strengen og 3)
lengden til strengen som bestemmer tonehøyden. Generelt vil da tonehøyden øke når tykkelsen blir mindre, når strengen blir strammere og når strengen blir kortere.

2 Lydbilde og frekvens med mikrofon og oscilloskop
Utstyr Oscilloskop er et måleinstrument som viser spenningsvariasjoner i et tidsperspektiv (En DM med lydkort kan gjøre det samme og derfor er øvelsen aktuell i skoleverket). En mikrofon omdanner
lydbølger til spenningsvariasjoner og sammen med et oscilloskop kan vi få et tidsbilde av ulike lyder (tid langs x-aksen og amplitude/trykk langs y-aksen).
Innstilling av oscilloskopet: Hvis bølgene på skjermen er for høye eller lave kan man vri på Volt/div til inngang A. Om man vil finne frekvens til en tone kan man vri på Time/div slik at en bølgelengde strekker seg over flere ruter. Pilen peker da på en tid (eks: 0,5ms)
som da er den tiden som markøren/lyspunktet bruker for å passere en rute. Hvis vi så ser at en bølgelengde svarer til f.eks. 4,5 ruter så vil svingetiden for den aktuelle bølgen være:

Skisser
av noen lydbilder fra ulike lydkilder slik de fremkommer på oscilloskopskjermen
i oppsettet ovenfor.
Litt mer om utstyr.
På illustrasjonsfotoet ovenfor har vi
brukt en mikrofon/høytaler fra en eldre telefon og to krokodilleledninger.
Denne mikrofonen har vel lav ohm-verdi og under selve forsøket brukte
jeg en liten høytaler større
ohm-verdi (150W) og koblet krokodilleklemmer direkte
på pluggene fra oscilloskopkabelen. Høyere ohm-verdi på en
spole i en høytaler betyr flere vindinger og det betyr igjen større
spenning som da er det som et oscilloskop måler. Bølgene
på skjermen ble med andre ord større og finere når jeg byttet
til høytaleren. Ellers vil et slikt oscilloskop også motta forstyrrelser
fra lysnettet og andre elektromagnetiske bølger og slike forstyrrelser
minskes om man ikke har for lange uskjermede ledninger. På bildet representerer
krokodilleledningene to slike uskjermede ledninger. Derfor erstattet vi krokodilleledningene med krokodilleplugger og skissen
til venstre viser da noen eksempler på hva vi fikk se på oscilloskopet.
En stemmegaffel brukes fordi den gir harmoniske (tilnærmet sinusformede)
og stabile (en bestemt frekvens og varer en stund) bølger uten overtoner
som er forsøkt vist på skissen til venstre. Da de første
forsøkene ble gjort stod tidsbryteren på 1ms pr rute og skissen
viser da at en bølgelengde er litt lenger enn 1ms. (Ca 10 bølgelengder
pr 9 ms = 0,9 svingninger pr ms som svarer til 900Hz). På stemmegaffelkassen
stod det 870Hz.
En fløyte som liknet på en orgelpipe av tre gav på
sin side en tone med en typiske overtone slik som vist på skissen.
Det var da tre smale topper for hver bred topp og det forteller oss da at overtonen
har tre ganger så høg frekvens.
En fiolinstreng ga da på sin siden en tone som tilsynelatende
hadde en "undertone" siden hovedbølgen gikk litt opp og ned.
Merk ellers at det på et oscilloskop ofte blir flere kurver fordi det
stadig kommer nye signal inn og om disse ikke er like vil de bli sideforskjøvet
i skjermen (triggeproblem). Brukes en datamaskin vil man derimot kunne lagre en bølge (sample)
og slipper da forstyrrelser av etterfølgende lyd.
Plystring gav også flere bølger og årsaken er at
man ikke klarere å lage en tone med helt stabil frekvens.
Om man stiller ned tidsbryteren slik at det lysende punktet bruker f.eks.
10 ms pr rute kan man vise hvordan lydstyrken varierer med tida. Et klapp
vil f. eks starte med et kraftig utslag (direktebølgen) mens de svakere
signalene som følger etterpå skyldes sannsynligvis refleksjoner fra
vegger og tak. Hosting har et mer jevnt tidsforløp, men begge
kan karakteriseres som hvit støy fordi de inneholder svært
mange ulike frekvenser
Ulike grafiske fremstillinger av lyd.
De skissene som er vist ovenfor
viser intensitet (langs y-aksen) som funksjon av tida (langs x-aksen). Dette
kan vi da kalle et tidsbilde av den aktuelle lyden. Om man bruker
datamaskin i stedet for oscilloskop og viser "lydbilder" er det vanlig
at man i tillegg til dette tidsbildet også kan få vist et annet lydbilde. Dette
andre kan vi kalle kalles frekvensspekter. I dette tilfellet vil datamaskinen
fordele ulike frekvenser eller tonehøyder langs x-aksen. I begge tilfellene
vil y-aksen fortsatt angi intensitet eller lydstyrke. Slike
frekvensspekter finnes da ofte på dyrere musikkutstyr og lydprogram i datamaskiner. Basstoner
fremkommer da som bevegelige søyler i ene enden mens diskanttoner fremkommer
som bevegelige søyler i den andre enden av x-aksen.
Måling av bølgefenomen
Tabellen nedenfor viser hva vi
kaller frekvensverdiene og styrkeverdiene i forbindelse med tre typer bølger.
Til høyre har vi så skissert ulike måleinstrument som det er mulig
å kjøpe for en rimelig pris.
|
|
Vannbølger
|
Lyd
|
Lys
|
Amplitude
|
Bølgehøyde[m]
|
Lydstyrke[dB]
|
Lysstyrke[lux]
|
Frekvens
|
|
Tonehøyde[C,D..]
|
Farge[Rød,Orange.]
|
Grovt sett kan vi si at et luxmeter (lysmåler) koster fra kr 100,- og oppover. En gitar-stemmer som kan måle visse tonehøyder koster fra 500,- og oppover. En desibelmåler (støymåler) koster fra 1000,- og oppover.
Støymåler
En
støymåler måler lydstyrken eller energien i lyden. Øret
vårt oppfatter ulike frekvenser ulikt sterkt og derfor er en støymåler
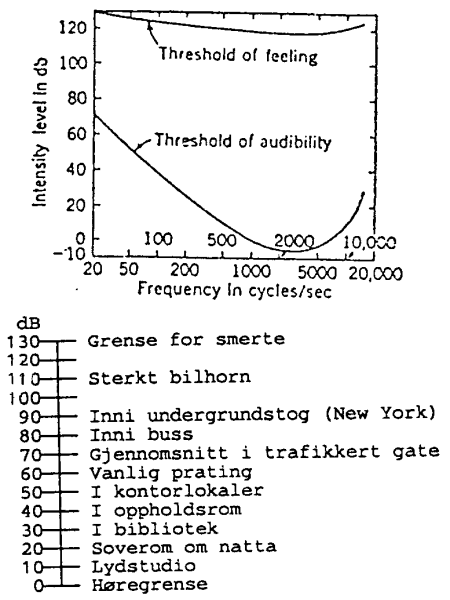
vanligvis kalibrert etter ørets følsomhetskurve som er vist til
høyre. Den
nedre kurven viser da nedre grensen for hva vi hører under normale forhold. Den viser da
at vi har størst følsomhet for lyd med frekvens omkring 3000 Hz. Merk at dB (desibel) er en logaritmisk størrelse og energien i lyden dobles da for hver 3 dB man beveger seg oppover langs skalaen. Tabellen under
gir en oversikt over typiske lydstyrker i ulike sammenhenger.
Lyd kan forsterkes og få lenger rekkevidde:
-ved styring v.h.a. skjerm (øretrakt,
parabolspeil ol.)
-gjennom rør (stetoskop, koridorer)
-ved hjelp
av resonanskasse
Lyd
kan dempes ved å unngå reflekterende flater. Der det er vegger og tak kan man så kle disse med porøse stoff
og belegg med mange hull som da reflekterer minst mulig lyd.
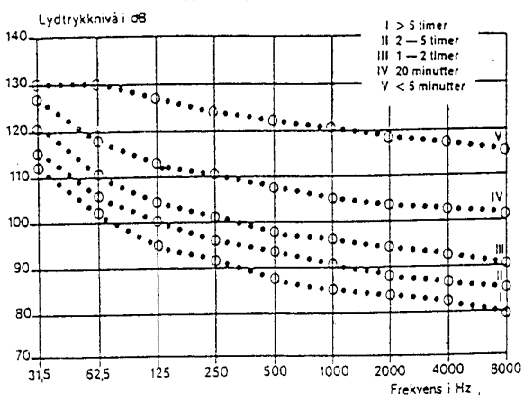
Figuren til venstre viser noen grenseverdier som gjelder for støy i yrkessammenheng. Merk
at vi tåler mindre av lyder med høy frekvens enn lyder med lav
frekvens. Det er heller ikke så farlig med sterke lyder om varigheten er kort.
Langvarig sterk lyd er derimot skadelig slik skjemaet viser.
Frekvensmåler
Frekvensmåling i forbindelse med
lyd er mindre aktuell, siden man sjeldent har behov for å vite nøyaktig
frekvens til en tone. I musikk er det imidlertid viktig at ulike instrumenter
er stemt rett i forhold til hverandre. I slike tilfeller kan man bruke en gitarstemmer. Funksjonen til denne er da at den varsler om en tone
er litt over eller under en bestemt standardverdi.
Hvordan bruke en datamaskin til å studere lyd:
Tonegenerator
|
På Internett
kan man finne et enkle tonegenereringsprogram. Eks:
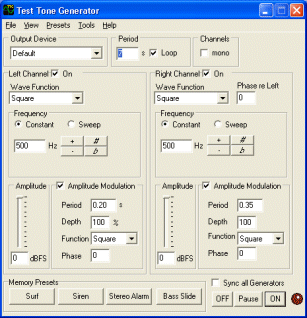 Test
Tone Generator V3.8
Test
Tone Generator V3.8
The Test Tone Generator (TTG)
turns the PC into a function generator for testing or demonstration, sound
tuning, education, for sound effects and other purposes. It can produce constant
or 'swept' test signals in real time. You can also save the signal as a .WAV file, e.g. to burn a test
tone CD.
|
Med en slik tonegenerator kan man
demonstrere ulike frekvenser og lydstyrker til ulike typer bølger fra harmoniske
sinusbølger til hvit støy. Det er også mulig å blande to toner og
demonstrere fading og hva slags toner som klinger godt sammen (harmonier).
Oscilloskop-program
|
Et gratis
oscilloskop-program fra Moscow
State University som kan lastes ned fra Internett (90618
bytes) og det er fritt for hvem som helst å bruke det på eget ansvar.
Digital Oscilloscope Uses PC Sound Card for Input 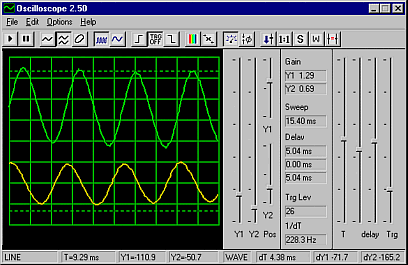
Overview
Oscilloscope for Windows is a Windows application that converts
your PC into a powerful dual-trace oscilloscope. Oscilloscope uses your PC's
sound card as an Analog-to-Digital Converter (ADC) to digitize any input
waveform (speech, music, electric signal, etc.) and then presents it on the
monitor in real time, allowing the user to control the display in the same way
as on a conventional "standalone" scope, for example change gain, timebase or
plot Lissajous patterns.
|
Med et slikt program kan vi få en grafisk framstilling av ulike lydbølger
i amplitude-tid-diagram og amplitude-frekvens-diagram (lydspekter)
og bestemme frekvens og lydstyrke-forhold.







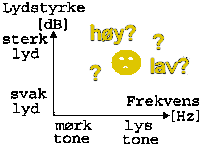






















 Test
Tone Generator V3.8
Test
Tone Generator V3.8