Mekanikk
4.11.03 Erling Skaar
Bygger på Emne 1 (krefter)
Hva er mekanikk?
Historien
bak SI-systemet
Krefter
Begrepene
kraft og akselerasjon
Newtons lover
Flo
og fjære
Corioliskraften
Massefart
og dreiemoment
Hva er mekanikk?
Ordet mekanikk betyr læren om bevegelse og likevekt. Av og til blir mekanikken oppdelt i statikk og dynamikk. Statikken handler da om likevekt og ting som er i ro. I konstruksjon av ulike byggverk er da statikken en sentral vitenskap. Statikken er da i hovedsak behandlet i fysikkement F1 Krefter. Dynamikken handler om sammenhenger mellom krefter og bevegelser. Denne delen er f.eks. sentral når man skal lage ting som beveger seg. Mekanikken handler om det vi ser omkring oss og slik sett kan mekanikkforståelse være nyttig i dagliglivet. I praksis kan vi si at mekanikken består av noen sentrale begrep og lovmessigheter som hjelper oss med å forstå naturen, og utnytte den til vårt eget beste. Newtons lover kan oppfattes som grunnlovene i mekanikken, og disse vil vi komme tilbake til seinere. Her vil vi imidlertid understreke at begrepsforståelse er viktig for å forstå mekanikken. Om vi ikke forstår begrepene som brukes, vil vi sannsynligvis heller ikke forstå Newtons lover. Derfor vil vi starte med noen sentrale begrep innenfor mekanikken.
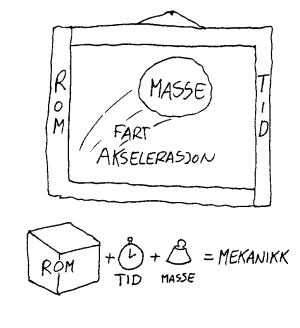
Et oversiktsbilde over mekanikken
For mange er det vanskelig å skille det sentrale i mekanikken fra "alt det andre". Vi vil her prøve å bygge opp en forståelse
for mekanikkens grunnprinsipp. Hva handler så mekanikken egentlig om? Grunnstørrelsen i mekanikken er masse. Mekanikk er på
en måte et resultat av at noen har plassert masse i rom og tid. Denne massen kan så bevege seg i rommet. I mekanikken er vi nettopp interessert i å forklare eller forutsi slike bevegelser. To begrep er grunnleggende når det gjelder å beskrive bevegelse. Disse er hastighet/fart og akselerasjon. Rammen omkring mekanikken er da rom og tid. I denne rammen har vi så ha en eller flere masser som beveger seg i forhold til hverandre. Klarer vi å ha denne rammen klart for oss mens vi arbeider med mekanikk, og ikke la oss distrahere av de mange forstyrrende faktorer som vi finner i alle virkelig situasjoner, så vil kanskje ikke mekanikken oppleves så vanskelig eller "mystisk".
Naturforståelse er nyttig i mange sammenhenger
Anta at en mann forteller at han så noe
som liknet en stein som "falt" oppover isteden for nedover. I en slik
situasjon vil mange søke etter grunner for å stemple mannen som upålitelig. Vi
vet jo at steiner ikke kan sveve, og derfor kan vi stemple hendingen som umulig. Men
er egentlig dette den beste måten å møte andre mennesker.
Om vi derimot tenker på det som mannen så som en masse som beveget seg "mot" tyngdekraften så er ikke det noen umulighet. Forutsetningen er imidlertid at det som beveget seg var "letter" enn luft. Det kan med andre ord være at mannen så en ballong fylt med helium som var malt slik
at den så ut som en stein. En dypere mekanikkforståelse kan kanskje bidra til å gjøre livet enklere i stedet for å skape mistenksomhet og forvirring.
Bakgrunnen for å trekke fram dette eksemplet er en erfaring om at det
er at det er få steder man møter så mye dogmatisme som nettopp
innenfor mekanikken. Når mange mennesker opplever at mekanikken er vanskelig
så har det sammenheng med at mekanikken har innebygget i seg noen tankemessige
problem som noen prøver å bagatellisere. Det er særlig de
som går for å være eksperter på fysikk som har problemer
med å forstå disse problemene og det er kanskje nettopp derfor at
de blir dogmatiske og avvisende når noen påpeker ulike svakheter
i tradisjonell mekanikkforståelse.
Mekanikk-tenkemåten
Begrepsbruk i dagliglivet
Når vi skal forklare eller beskrive noe, bruker vi vanligvis ord eller begrep som tilhørerne forstår. Hvis tilhørerne ikke forstår de ordene som brukes, vil de heller ikke forstå det vi prøver å formidle. Et utsagn som: "Jeg drakk et glass melk til frokost" vil umiddelbart bli forstått av en som forstår norsk. Tilhøreren oppfatter umiddelbart budskapet i setningen fordi situasjonen som beskrives er velkjent og begrepene er brukt på en vanlig måte.
I fysikken bruker vi også vanlige ord og begrep, men mange vil ha problemer med å forstå beskrivelser og forklaringer hvor fysikk er tema. En grunn kan være at vi ikke har noen direkte erfaringer med det som beskrives. I slike tilfeller vil ofte praktiske erfaringer med fysikkutstyret være en god hjelp. Men det at fysikk oppleves vanskelig av mange, kan også skyldes at det kreves en relativt grundig forståelse av begrepene som brukes. Vi må med andre ord beherske begrepene på en slik måte at vi blir uavhengig av konkrete forestillinger og egne erfaringer. Begrepsforståelsen må på en måte "renses" fra distraherende "krykker" og "bandasje". En baby som første gang får høre at en lang gul ting heter blyant vil kanskje tro at alle lange gule ting er blyanter. Etterhvert vil barnet kanskje erfare at det finnes røde blyanter, og at et viktig kjennetegn på en blyant er at vi kan skrive og tegne med den. Farge og form blir da mindre vesentlig. Kanskje fungerte barnets første blyant-begrep tilfredsstillende innenfor lekerommets fire vegger en lang stund, men før eller siden vil barnet lære voksnes forestilling om hva en blyant er.
I fysikken finnes det noen grunnleggende begrep. En rett forståelse av disse er viktig for å forstå fysikken. Ofte er det et langt og møysommelig arbeid å lære grunnleggende begrep da det ofte innebærer en "avlæring" av misforståelser og unødvendige hjelpeforestillinger som man har adoptert underveis. Dessuten kan nok avstanden mellom læringen av grunnbegrepene og konkrete erfaringer synes vel lang av og til. En for rask progresjon kan medføre at vi får "hull i kunnskapen" som vil hindrer videre læring og forståelse. Hvilke begrep er så grunnleggende i naturfag? Her vil vi gi en kort analyse av utsagnet setningen ovenfor som illustrerer hvordan man tenke i naturfaglig sammenheng. Utsagnet handler om et stoff som heter melk. Dessuten sier utsagnet noe om hvor mye melk som ble drukket. "Et glass" angir et bestemt volum, nemlig det volumet som er i et glass. Et annet ord for volum er rom. Selv om det ikke er sagt direkte vil vel de fleste regne med at den aktuelle handlingen foregikk hjemme. Dette er videre et sted i rommet som kan angis nærmere ved hjelp av en adresse. Utsagnet forteller også noe om når begivenheten skjedde. Selv om "til frokost" er en litt upresis tidfesting så gir den likevel en tid for hendelsen. Utsagnet "Jeg drakk" er handlingsdelen av uttrykket. Alle handlinger forutsetter at det er energi eller kraft til stede. I dette tilfellet finner vi årsaken til kraften hos jeg-personen, og det er et glass med melk det går ut over. Denne lille analysen har frembragt fire grunnleggende begrep (både volum og sted er knyttet til rom og grunnstørrelsen meter). Det er de samme begrepene vi finner igjen i all fysikk, og et viktig mål for den som studerer fysikk bør da være og raskest mulig å kunne skille ut det som er kjernen i et utsagn og å bruke minst mulig til på perifere ting.

Strukturer i mekanikkemnet
Er det så mulig å si noe generelt om tankestrukturene innenfor emnet mekanikk? Hva tenker en som behersker dette fagområdet? Basis for alle katalogiseringer er uavhengige kategorier. Hensikten med katalogisering er struktur og rask gjenfinning og enklere bruk. Et eksempel:
Skal vi kjøpe planter til en hage kan det være nyttig å kunne søke etter følgende kategorier: Størrelse, farge og blomstringstid. Vi har ofte et ønske om ulike farger, ulik størrelse og ulik blomstringstid. Det kan f.eks. være aktuelt å søke etter en liten blå blomst som blomstrer seint som skal passe sammen med noen andre planter vi har der fra før. I mekanikk kan vi lage noe tilsvarende. Nedenfor nevner vi tre uavhengige kategorier som er nyttige i mekanikken.
1) For det første kan vi tenke oss en inndeling som går på graden av forenkling. Naturen består av ulike gjenstander med utstrekning og form. Ofte vil fysikere forenkle gjenstander til punktpartikler. I praksis vil det si at vi ser bort fra utseende og størrelse. Dette medfører at faktorer som dreiing og luftmotstand blir neglisjert. I de tilfellene at dreiing eller areal/volum er sentrale for forståelsen av det som skjer snakker man ofte om stive legemer som er forenklet til kuler, sirkler eller andre geometriske figurer som er enkle å beskrive matematisk. Det er da mer komplisert å beskrive krefter og bevegelser i forbindelse med slike partikler. I andre tilfeller finnes det mange partikler som vi må ta hensyn til. Et slik system kalles ofte mangepartikkelsystem. Gasser er et eksempel på noe som kan beskrives som en samling av mange små partikler. I stedet for å konsentrere seg om hver enkelt partikkel kan vi betrakte mange partikler som en enhet. Vi kan f.eks. oppfatte begrepet trykk, som er et resultat av støt fra mange partikler, som et resultat fra en gass. Vi formulerer altså lover og regler som gjelder en mengde enkeltpartikler under ett.
2) En annen måte å dele inn mekanikken, er å skille mellom det som er i ro (statikk) og det som beveger seg (dynamikk). Statikken er da enklest, siden det her ikke skjer noen endringer over tid. Vi har altså "god tid" til å konsentrere oss om krefter, strekk, press og liknende. Fart og akselerasjon er sentrale begrep i dynamikken.
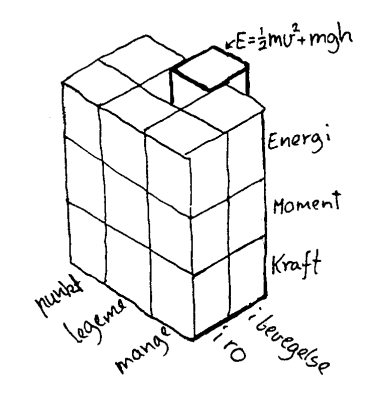
3) Et stikkord for den siste kategorien er "synsvinkel". Vi kan altså se på et fenomen fra ulike synsvinkler eller vektlegge ulike sider. Disse tre synsvinklene er karakterisert med tre begrep: kraft, moment og energi. Disse begrepene er ikke uavhengige av hverandre. De oppfører seg imidlertid litt ulikt i ulike situasjoner. Når vi skal analysere en situasjon, kan vi da velge det begrepet som er enklest å bruke i den aktuelle situasjonen. Dette er en hovedårsak til at vi operer med tre ulike begrep selv om et av begrepene hadde vært nok for å beskrive alle situasjonene. Energi er f.eks. et mer kompleks begrep enn kraft. På grunn av at energien er bevart i mange prosesser vil imidlertid energien oppføre seg på en mer oversiktlig måte enn kreftene i disse prosessene. Det er da ofte enklere å bruke energilikninger enn f.eks. Newtons lover.
Skjemaet under gir en oversikt over mekanikken dette heftet i forhold til kategori 2 og 3:
|
|
1KRAFT |
2MOMENT |
3ENERGI |
I RO |
Krefter (F) |
Vektstenger |
(Fjær) |
BEVEGELSE |
Krefter (F) |
Massefart |
Arbeid(W) |


Litt om begrepene stoff og legeme
Nå vi snakker om et legeme eller en partikkel mener vi oftest noe bestemt. Men det er ikke sikkert at alle mener det samme. For å sikre at vi bruker begrepene likt kan en begrepsoppklaring være nyttig i mange tilfeller. En begrepsoppklaring inneholder vanligvis:
1) Et forsøk på å skille noe fra andre tilstøtende begrep.
2) Presisere hvilke egenskaper som er sentrale for det aktuelle begrepet.
Her vil vi kort se på noen generelle sider ved begrepet stoff som kan være nyttig når vi skal definere hva vi mener med et legeme. Alt vi omgir oss med kan vi kalle stoff. Stoff kan som kjent forekomme i gassform, væskeform og fast form. Begrepet legeme vil vi her definere som en avgrenset mengde med fast stoff. For å illustrere at grensen mellom fast stoff og væske kan være litt "flytende", vil vi kort nevne to begrep som brukes i denne grenseoppgangen. Et legeme kan være mer eller mindre elastisk. Ei stålfjær eller et strikk er eksempler på stoff som er elastisk. Med elastisk mener vi at legemet til en viss grad kan omformes av krefter. Men når kreftene slutter å virke så vil legemet få den opprinnelige formen tilbake. Et annet begrep er plastisitet. Et legeme som over tid kan deformeres er plastisk. Jo fortere deformeringen kan foregå, jo mer plastisk er stoffet. Eksempler på slike stoff er honning og sirup. De er altså stive i forhold til brå påvirkning, men på lang sikt kan det "flyte som ei væske".

Om å "se" fysikk
Noen oppfatter fysikk som noe
vanskelig som forvirrer mer enn det oppklare. Årsaken kan være at
dårlige lærere som ikke har klart å videreformidle kjernen
i fysikken. Hensikten med fysikken er ihvertfall å forenkle forståelsen
av omgivelsene våre, og de som har forstått fysikk vil nok bekrefte
at det er dette som skjer når vi lærer fysikk. Her vil vi se litt nærmere på hva det er som skiller en fysiker fra en som synes fysikken er "fjern" og vanskelig.
Galilei, en av Newtons forløperer, la grunnlaget for den vitenskapelige revolusjonen som kom senere. Han vokste opp med samme virkelighet som alle andre, og sannsynligvis tenkte han omtrent som de andre i sin samtid. Hva var det da med Galilei som gjorde at han "oppdaget" mekanikkens grunnlag? Ytre sett gjorde han visse ting som få andre gjorde. Han brukte f.eks. mye tid til å slippe ulike ting i tyngdefeltet. De som observerte dette syntes kanskje det var bortkastet. De visste allerede at ting som slippes vil falle eller trille langs et skråplan. Videre visste de at ei fuglefjær ville falle seinere mot jorda enn en stein. Hva er det da som skilte Galilei fra en hvilken som helst annen original som gjør uvanlige ting. Det er vanskelig å si noe sikkert om dette, men kanskje er følgende punkter viktige:
1) Galilei var ikke fornøyd med å bare konstatere hva som skjedde i ulike situasjoner. Han søkte etter generelle sammenhenger som kunne forklare mer en enkeltstående tilfeller. Dette skjedde da gjennom praktiske forsøk og eksperiment.
2) Galilei konsentrerte seg om enkle sentrale begrep. Han forenklet det han så til å dreie seg om legemer (ikke stein trekuler osv.) som beveget seg. Massen var videre den sentrale egenskapen ved de ulike legemene. Å konsentrere seg om massen til ulike legemer, er en form for abstraksjon som kan være vanskelig i starten. I lengden kan imidlertid slike metoder vise seg fruktbare. En av årsakene til vitenskapens suksess er at den har innført endel mer eller mindre abstrakte begrep.
3) Videre klarte han å skille ut og isolere de ulike faktorene som påvirket bevegelsene. I praksis kunne ikke Galilei fjerne luftmotstanden eller tyngdekraften. Men ved å gjøre forsøkene på bestemte måter og bruke en matematisk tilnærmingsmetode, klarte han imidlertid å skille de enkelte faktorenes bidrag fra hverandre. Ved hjelp av tall og figurere på et papir er det mulig å lage en slags abstrakt idealisert virkelighet. I en slik virkelighet ble bevegelsene "enklere" enn de bevegelsene vi observerer til daglig. Det var derfor lettere å "se" de sammenhengene som finnes mellom ulike begrep ved hjelp av tall på et papir.


Om å lære fysikk i grunnskolen
Noen tror at elevene lærer fysikk bare ved å gjøre eksperiment. Hjernen vår vil alltid huske inntrykk den får en viss tid. Om noen mener at vi lærer fysikk når vi husker eksperiment eller spesielle hendelsesforløp, så vil de kanskje oppleve det
som er skrevet her som unødvendig for en som har tenkt å bli lærer i grunnskolen. En sentral idé i dette heftet er imidlertid at fysikklæring er noe mer enn å huske eksperimenter og formler. Å lære fysikk er en form for konstruksjon
av tankebygninger. Det betyr at praktiske forsøk i seg selv ikke er noen garanti for nyttig læring. Konstruktivismen er navnet på en pedagogisk teori som prøver å beskrive hva som skjer ved læring. Her vil vi bare nevne at et kjernepunkt i denne teorien er at læring er en aktiv prosess fra elevens side hvor han selv konstruerer de aktuelle tankestrukturene. Læring er altså ikke en automatisk konsekvens av mye informasjon i form av tekst, figurer og forsøk.
Undersøkelser om fysikk-kunnskapene i ulike folkegrupper, viser at det ikke er noen selvfølge at vi lærer fysikk av å leve i en virkelighet som er styrt av fysiske lovmessigheter. Dette er grunnen til at vi her vil konsentrere oss litt ekstra om hva det vil si å "tenke fysikk". Fysikere lærer fysikk av naturen som omkring oss, men det er en misforståelse å tro at vi lærer fysikk kun ved å oppholde oss i naturen. Vi blir ikke en hest om vi sover i en stall. Vi lærer eller husker mye konkret når vi opplever naturkreftene på nært hold, men dette er ikke nødvendigvis fysikk i vår betydningen. Her vil vi definere fysikkunnskap som strukturert tankevirksomhet knyttet til naturen som omgir oss.
Er det fysikken eller begrepene som er vanskelig?
Når fysikk har vist seg å være vanskelig å fatte for elever i grunnskolen, kan det ha flere årsaker. På den ene siden kan selve naturlovene være så kompliserte at det er vanskelig å forstå dem
eller å skjønne de praktiske konsekvensene av dem. Som vi vil se seinere, er naturlovene
svært enkle når vi uttrykker dem i en matematisk språkform. Begrepene som brukes er konsekvent og logisk og vi slipper å plages med mange unntak eller forklarende tillegg
som man ofte trenger i Norges lover. Det betyr at det kanskje ikke er selve naturlovene som skaper problemer i skolen. En annen mulig årsak til problemene i skolen kan
være selve begrepene som brukes. Å forstå fysikk vil bl.a. si å ha en dypere forståelse for de grunnbegrepene som brukes. En overfladisk delvis misforstått forståelse av begrepene kan skape forvirring isteden for forståelse i møtet med naturfagundervisningen. Dette er hovedgrunnen til at vi her
bruker relativt mye tid på begreper kraft.

Bør grunnskolelærere lære mekanikk
I dette heftet vil vi legge vekt på å skape en forståelse for ulike begrep ved hjelp av ord og praktiske eksempler. Et hovedmål har vært å få fram at disse begrepene er relevante for
oss og ikke fjerne fra virkeligheten vår som mange synes å tro. Nå er det ikke alle elever i grunnskolen som vil få behov for å fordype seg i disse begrepene etter grunnskolen, men de som skal studere videre trenger ofte endel
fysikkunnskap. Nå er det videre en fare for at elever i grunnskolen får innarbeidet feil forestillinger, som kan skape endel problemer i senere skolegang. I denne sammenhengen kan det også tenkes at lærere med manglende forståelse for disse begrepene kan være medvirkende årsaker til at elevene lærer feil som skaper barrierer og kanskje negative følelser når elevene møter dette stoffet igjen seinere.
Her vil vi ikke argumentere for en grundig behandling av mekanikkbegrep som krefter ol. i grunnskolen. Det er imidlertid ikke mulig å unngå situasjoner hvor slike begrep er aktuelle. Et mål burde da være at lærerne i grunnskolen og førskolen har så mye fysikkbakgrunn at de ikke gir elevene feil forestillinger om med de aktuelle fysikkbegrepene. Når elevene kommer i videregående skole forventer vi at de kan grunnleggende ting innenfor f.eks. matematikk og norsk. Dette er da en forutsetning for å kunne fordype seg i ulike fagfelt. Dessuten viser erfaringer at vi lærer grunnleggende ting lettest før vi blir tenåringer. I fysikk gjelder sannsynligvis noe tilsvarende. I praksis har det ofte vært slik at lærere unngår fysikktemaer i småskoletrinnet og i førskolen, fordi lærerne tror det er for vanskelig. Erfaringer har imidlertid vist at det er vanskelig å starte fysikkundervisningen på ungdomstrinnet eller videregående trinn, om det ikke er lagt et grunnlag tidligere. Kanskje har det sammenheng med at hverdagsforestillinger da har "grodd fast".
Om vi ønsker en fysikkundervisning i norsk skole er vel følgende punkter sentrale:
* Fysikkemnene må få tildelt sin rettmessige plass i naturfaget. I dag er det ting som tyder på at enkelte elever får svært lite fysikkundervisning fordi lærere prioriterer andre emner (eks biologi).
* I tillegg til tradisjonell "lesing i lærebok og svar på spørsmål" bør det også være plass til praktiske forsøk, slik at elevene forstår at lærestoffet handler om virkeligheten.
* Elevene trenger hjelp til å "tenke fysikk".
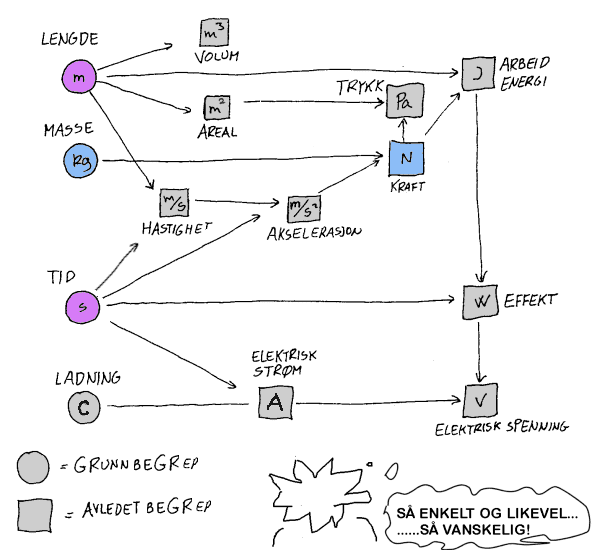
Historien bak SI-systemet
Noen mennesker har problemer med å strukturere livet. Andre har problemer med å se strukturen i de ulike skolefagene. Erfaringer viser vel at de som har funnet strukturer er de som behersker livet og skolehverdagen best. Hensikten med figuren over er å vise den forholdsvis enkle begrepsstrukturen som finnes i fysikken. Det er da snakk om internasjonalt standardiserte størrelser (SI-størrelser) som man har blitt enige om å bruke og som man har klare og entydige definisjoner av. Å lære fysikk handler om å skaffe seg en oversikt over endel begrep som så i neste omgang gjør at man kan finne svar på ulike spørsmål knyttet til omgivelsene våre. I figuren viser pilene hvordan ulike begrep er definert (fra grunnbegrep mot utledede begrep) og vanligvis kan vi også følge disse pilene når vi skal finne konkrete verdier på de ulike kvantitative størrelsene. Hvis vi f.eks. skal finne hvor fort vi går, kan vi måle en lengde og tilhørende tid og finne farten ved å dividere meter på sekund. De to begrepene som er markert med blått (masse og kraft) er da de som er knyttet til kraftbegrepet og som vi i dagliglivet ikke skiller så klart mellom. Grunnlaget for målinger av disse størrelsene er begrepene lengde og tid.(markert med fiolett). Her følger et historisk tilbakeblikk som forhåpentligvis viser behovet for en slik standardisert struktur for de målbare størrelsene som vi finner i omgivelsene våre.
Det er ikke snakk om å pugge SI-systemet som er vist ovenfor, men sannsynligvis vil en slik oversikt være til hjelp når man prøver å se strukturer i det man lærer. I undervisningssammenheng er det videre viktig at elevene får øving med å bruke disse størrelsene tidligst mulig i grunnskolen. De er på en måte grunnleggende for forståelsen av naturen selv om ikke alle er grunnbegrep i vanlig forstand. (Kraft er ikke et grunnbegrep i SI-systemet, men det er sannsynligvis et grunnleggende begrep i en opplæringssituasjon hvor det er snakk om å forstå naturen).
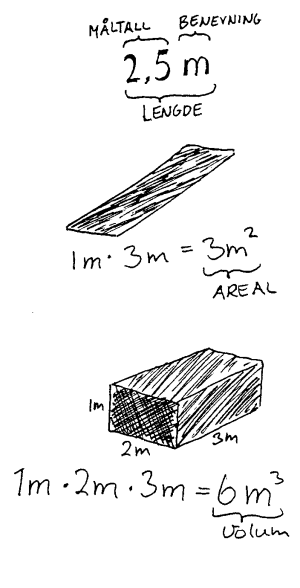
Rombegrepene
lengde, areal og volum
Vi har tre rom-begrep. Disse er lengde, areal og volum. Av disse kan vi si at lengdebegrepet er det mest grunnleggende. Standardenheten for lengde er meter (m). De to andre enhetene er da utledet utfra lengdebegrepet. Vi får areal om vi multipliserer meter med meter (m²) og vi får volum om vi multipliserer meter med seg selv tre ganger (m3). I fysikken er det viktig at vi forstår at lengde, areal og volum i prinsippet handler om "romdelen"
av tilværelsen vår. Disse begrepene sier da noen om posisjon eller størrelse i rommet.
I mekanikken er det videre vanlig å tenke seg at rommet kan eksistere uavhengig av om det finnes noe i det eller ikke. Det
finnes med andre ord et absolutt rom som er uavhengig av det som er i rommet. Dette
kan diskuteres, men var da Newton som foreslo dette og i undervisningsammenheng
er det vanlig å tenke på rommet som noe som er uavhengig av det
som befinner seg i rommet.
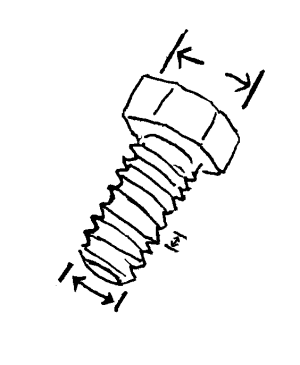
Bestemte mål på ulike gjenstander
Mye av det vi omgir oss med til daglig forekommer i bestemte mengder eller dimensjoner. Skruer og muttere finnes i mange forskjellige dimensjoner. Skal vi gjøre bruk av disse på en effektiv måter er det ikke nok å vite forskjellen på skruer og muttere. Vi må i tillegg vite litt om dimensjonene til disse. Om vi f.eks. skal bestille en skrue uten å ha en gammel skrue og vise til, må vi oppgi noen mål. For skruens vedkommende må både diameter og sporbredde være rett for at de skal passe i en mutter. Dessuten er vi også interessert i diameteren på hodet for å sikre oss at vi har fastnøkler som passer til aktuelle skruer. For å sikre at ting fungerer slik det skal er det nødvendig at både produsent og bruker har en felles måleenhet som de holder seg til. Dessuten er det viktig at de foretar målingene tilstrekkelig nøyaktig. I noen situasjoner er det spesielt viktig at målingene er nøyaktig. I andre situasjoner er det ikke så viktig. Uansett hvordan vil måler, vil vi aldri oppleve at vi klarer å måle med 100% nøyaktighet. Derfor opererer vi med begrepet usikkerhet når vi oppgir et mål. Denne usikkerheten kan f.eks. skyldes dårlig utstyr eller ulike forstyrrelser. Dette kaller vi med et fellesnavn for feilkilder.


Konvensjoner/avtaler er nødvendige
For å oppnå en felles målenhet
(standard), trenger vi en avtale som alle holder seg til. I tidligere tider da kommunikasjonen mellom folk var dårligere enn i dag, hadde hvert folk sine måleenheter. Dette skapte endel
problemer når det gjaldt samhandel og samarbeid mellom folkeslag,
men internt fungerte det som regel ok. Ofte ble målenhetene sett på som en del av kulturarven eller noe som skulle være med på å øke samfølelsen innenfor de ulike folkeslagene. Derfor var det motstand mot å samordne målenhetene. I Frankrike var det f.eks. i flere århundrer et ønske om "En konge, en lov, en vekt og et mål". Noen
foreslo da å knytte standardmålene til kongens fysiske legeme. Dette
ville imidlertid skape problemer siden en utskifting av konge sannsynligvis
også ville medførte endringer i standardmål.
Etter den franske revolusjonen foreslo biskop Talleyrand i 1790 at Frankrike skulle gå sammen med England om en felles lengdeenhet. Om alle parter er enige i slike forslag, er det ikke alltid like lett å komme fram til et konkret resultat. I England hadde Chr. Hygens like før foreslått at lengdeenheten skulle baseres på lengden til en sekundpendel. En begrunnelse for å la 1 m være lik lengden til en sekundpendel var å knytte lengde og tidsenheten sammen. Ulempen er at denne lengden er avhengig av gravitasjonskonstanten (tyngdens akselerasjon) som varierer litt omkring på jorda. Talleyrand kontaktet Academie des Sciences og de nedsatte en komite som kom med et alternativ. I 1971 anbefalte de at lengdeenheten skulle være fast knyttet til naturen, og en timilliontedel av en kvadrat av jordmedianen. Utgangspunktet for å bestemme jordmedianen skulle være nøyaktig målinger av avstanden fra Barselona i Nord-Spania til Dunkerque i Nord-Frankrike. Det ble ikke noe internasjonal enighet her da England og Amerika syntes den franske metoden var upraktisk. Behovet for en felles enhet vokste med den industrielle revolusjonen. Etter et fransk initiativ ble den berømte Convention du Metre signert i 1875. Da ble det enighet om å knytte meterdeinisjonen til en mal som ble oppbevart i Frankrike.
Lengdemålingens historie
Sumerne som hersket i Babylonia mellom 4000 og 2500 hadde et tallsystem som var basert på 60. Dette er opphavet til sirkelens gradeinndeling (360) og døgnets timeinndeling (24). En kopperstav som stammer fra ca 2000 f.kr. var 110,35 cm lang og var videre oppdelt i 4 fot, 16 håndsbredder eller 64 tommer. Senere har mange folkeslag brukt prinsippet om å knytte lengder til kroppsdeler. I Frankrike, England og Amerika overtok man også mål som var basert på kroppsdeler uten at man klarte å samordne disse før metekonvensjonen i 1875. Etter den tid har England og USA fortsatt
å bruke egne målenheter i tillegg til meteren. Fortsatt skaper dette problemer i ulike sammenhenger. I dag er ikke meteren definert
utfra et bestemt metermål som oppbevares i Frankrike, men utfra et bestemt antall bølgelengder av et bestemt lys.
Masse
På samme måten som ladning er et grunnbegrep i elektrisitetslæra, så
er masse et grunnbegrep i mekanikken,
men det er da ikke så uforanderlig som ladningen og det er da sannsynligvis
heller ikke så grunnleggende i naturen som ladningsbegrepet er. Standardsymbolet er m og standardenheten er kilogram (kg). Det
vi omgir oss med har ulik form og egenskaper. I
mekanikken forenkler man ofte virkeligheten og konsentrerer seg om masser som vekselvirker
med hverandre. Vi
bryr oss altså ikke om farge, ladning eller andre egenskaper ved det som omgir oss. Vi er primært opptatt av massen
til gjenstandene omkring oss. Hva er så masse? Nå er det vanskelig å gi en enkel definisjon av masse siden det er snakk
om et grunnleggende begrep. Det finnes altså ikke mer grunnleggende begrep
som vi kan bruke for å definere masse, og innlæringen av begrepet
vil da skje via bruk av begrepet i ulike sammenhenger. I praktiske sammenhenger er det viktig
å være klar over at masser ikke er vektorer (har retning) men de
har bare en tallverdi. Masse er med andre ord en skalar størrelse som kan være stor eller liten. Massen til de ulike stoffene er da avgjørende for hvordan de oppfører seg. Både i fysikken og i dagliglivet har masse en sentral rolle. Internasjonalt er man blitt enige om enheten kilogram (kg) for masse. Opprinnelig ble en kg definert som massen av 1 kubikkdesimeter vann ved 4 grader celsius. Det viste seg senere at denne ble for unøyaktig. I dag er 1 kg definert som massen av den internasjonale kilogramprototypen som oppbevares i Sèvres i Frankrike.
"Klokkene" som gir måneder og år
Massemålingens historie
Masse eller vekt har alltid vært viktig i samkvemmet mellom mennesker. Endel av de eldst pengesystemene var knyttet til massen av pengestykkene. Pengestykkene måtte derfor veies for å finne verdien av dem. Bibelen inneholder f.eks. advarsler mot å bruke feil vekter og det henspeiler da på at vi ikke skal fuske når vi handler. Etter revolusjonen i Frankrike var det et ønske om å utlede massenheter fra lengdeenheten. Først ble g
(gram) brukt som enhet, men det ble fort klart at denne enheten var vel liten i de fleste praktiske sammenhenger. Derfor gikk man over til kg (kilogram) som enhet. Denne ble definert som massen til en kubikkdesimeter vann. Så ble det laget et lodd av platina som ble oppbevart i Frankrike. Fortsatt er det et slikt lodd som definerer hvor tung en kg skal være. Det har ikke vært praktisk mulig å erstatte den med andre definisjoner som er uavhengig av prototypen som er plassert i Frankrike.
Tidsmålingens historie
I motsetning til de to foregående målenhetene er tidsenheten direkte forankret i naturen. Ifølge Bibelen ble sola og månen satt på himmelen for å vise tid (1Mos.1,14). Siden har døgn og år vært utgangspunktet for all tidsmåling. Sumerne regnet at året hadde 360 døgn og omløpstiden for månen var ca 30 dager. Det gir 12 måneder i året og disse tallene har nok også påvirket de som bestemte hvordan et døgn videre skulle oppdeles i timer og mindre enheter. Når det gjelder kalenderen, så er det et problem at jordas dreiing ikke er nøyaktig synkronisert som 1/30 del av månens rundetid og 1/360 av jordas rundetid. I år 400 f.kr. gikk romerne bort fra å knytte kalenderen til månen. I 1582 innførte pave Gregorius den XIII den kalenderen som vi har nå. Han innførte da
ordningen med skuddår for å unngå forskyvning i forhold til
årstidene. Dette innebærer at sommersolverv vil komme noenlunde fast på kalenderen fra år til år. Det er imidlertid innebygget en liten feil i vår kalenderen som tilsvarer 2 timer på 10000 år.

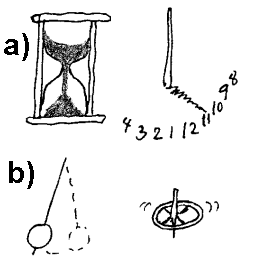
Klokker som viser a) timer og minutt b)minutt og sekund
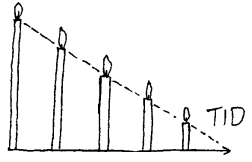
Et stearinlys brenner med fast hastighet (lineært)
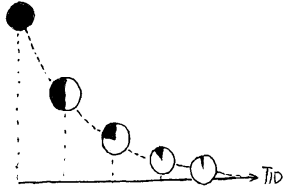
Radioaktive stoff har en fast halveringstid. Derfor "brenner" de ikke lineært.
Tidligere ble solur og timeglass brukt for å måle kortere tidsrom enn et døgn. Mekaniske ur ble sannsynligvis laget først i 1300 årene i Europa. Et eksempel på slike ur er pendeluret. Dette baserer seg på prinsippet om at pendelens svingetid er svært stabil. Skipstrafikken hadde tidlig behov for nøyaktige ur til hjelp i posisjonsbestemmelsen av lengdegrad. Pendeluret var dårlig i skip. Hvorfor? Pendelen ble derfor erstattet av koblede pendler eller hjul for at bevegelsen til klokka skulle påvirke dem minst mulig. I dag har vi stort sett forlatt de mekaniske urene og bruker elektroniske ur. Disse baserer seg på at elektriske svingninger er svært stabile i enkelte stoff (kvarts ol.). Et sekund ble først definert som 1/86400 av et middelsoldøgn. Nøyaktige målinger har imidlertid vist at jorda saktere litt av i dreiingen. I dag er et sekund definert som et visst antall svingninger av stråling fra et bestemt stoff. Fortsatt er vi imidlertid interessert i å la sola bestemme hva som er rett tid, og derfor må vi fra tid til annet stille klokkene for å synkronisere dem med sola når forskjellen er blitt for stor. Vi klarer ikke å "stille sola"!
Dateringsmetoder
Når vitenskapen skal bestemme alderen på ulike objekt, brukes en form for tidsbestemmelse som prinsipielt skiller seg endel fra vanlig tidtaking. Når ingen var til stede i starten og satte i gang en klokke eller avleste en verdi på en pålitelig klokke, må vi via omveier prøve å beregne startpunktet. Grunnlaget for alle slike beregninger er at det i naturen finnes prosesser som har en hastighet
som kan bestemmes. Et stearinlys vil f.eks. brenne nedover med en noenlunde jevn hastighet. Om vi så vet hvor langt det var når det ble tent,
kan vi beregne hvor lenge det har brent selv om vi ikke husker når det ble tent. Innenfor geologi og arkeologi er vi ofte interessert i å bestemme alder til objekt som er så gamle at mennesker ikke kan fortelle alderen. De såkalte radioaktive metodene er da vanlig. Disse metodene forutsetter at vi må anta noe om hvordan startbetingelsene var. Videre må vi anta at de aktuelle radioaktive prosessene alltid har hatt samme hastighet. Resultatet av slike beregninger blir derfor ikke sikrere en det de ovennevnte antakelsene.
Krefter
Se F01
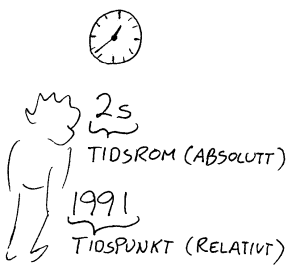

Hastighet regnes vanligvis i forhold til jorda.
Begrepene fart og akselerasjon
Tid
Også dette begrepet er behandlet i astronomiheftet, og derfor vil vi her bare kort repetere det som er viktigst i forhold til mekanikken. Standardsymbolet er t og standardenheten er sekund (s). Også i dette tilfellet skapes det minst problemer om vi antar at tid er et absolutt begrep. Det betyr f.eks. at tida fortsetter å gå selv om alle klokker stopper. Det betyr videre at klokker kan gå feil, men ikke selve tida. Ellers vil vi si at vi trenger begrepet tid for å beskrive bevegelser på en eksakt måte. Begrepene fart og akselerasjon hadde ikke vært til, om vi ikke hadde hatt begrepet tid. Det er altså først etter at vi har "definert" begrepene rom og tid, at vi kan vi definere begrepene fart og akselerasjon.
Fart
Fart eller hastighet har vanligvis symbolet v og benevning m/s. Fart er definert som strekning dividert på tid. Denne definisjonen kan uttrykkes på matematisk form:
v = s/t

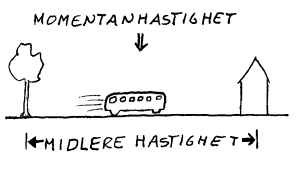
Fart eller hastighet regnes her på jorda vanligvis i forhold til jorda. Når vi snakker om hastigheter i solsystemet, regnes disse i forhold til sola. Hastigheter ellers i universet regnes i forhold til andre passende referansesystem. Dette betyr at fart er et relativt begrep. Farten til en gjenstand er altså ikke den samme uavhengig av hvem som observerer farten. Når vi skal oppgi fart, må vi også oppgi hva farten regnes i forhold til. Til vanlig er det jorda som er referansesystem for alle hastigheter og det er da underforstått når det ikke er spesielt nevnt.
I litteraturen finner vi ofte to ulike begrep for fart eller hastighet. Disse er:
1) Midlere hastigheten finner vi ved å dividere tilbakelagt veilengde med den tida som er brukt. Gjennomsnittsfart er et annet ord som uttrykker det samme.
2) Nå farten variere bruker vi ofte ordet momentanhastighet. Definisjonen sier at dette er en grenseverdi for midlere hastighet når tidsrommet vi måler over går mot 0. Her vil vi også si at et speedometer vil vise denne hastigheten. I dette kurset vil vi ikke gjøre noe poeng av dette skillet. Det viktigste er at vi kjenner den generelle definisjonen for hastighet og kan bruke denne i ulike situasjoner.
Akselerasjon
Akselerasjon er også et ord som beskriver en form for bevegelse. Akselerasjon er definert som fartsforandring pr. tidsenhet. Akselerasjon er en størrelse som kan være stor eller liten. Benevningen er m/s² og den viser at lengde og tidsbegrepet er involvert. Forsøk viser at akselerasjon alltid har en bestemte verdi. Den er altså ikke avhengig av observatøren og derfor sier vi at akselerasjon er en absolutt størrelse i universet. Om et legeme har en akselerert bevegelse, vil vi altså alltid finne en og bare en verdi for denne akselerasjonen. Et eksempel: Når noe dreier eller går rundt har vi en form for akselerasjon. Når vi ser at stjernehimmelen dreier i forhold til jorda, kan vi med sikkerhet si at det er jorda og ikke stjernehimmelen som dreier. Både værforholdene og det faktum at jorda er litt flattrykt ved polene, viser dette. Det oppstår altså krefter som kan måles når noe er akselerert. Vi skal komme tilbake til dette seinere. Her vil vi bare kort skrive opp definisjonsformelen for akselerasjon samt en utledet formel som viser gir akselerasjonen når noe går i en sirkelbane.
a = (v-v0) / t (definisjonsformel)
a = v² / r (sirkelakselerasjon)
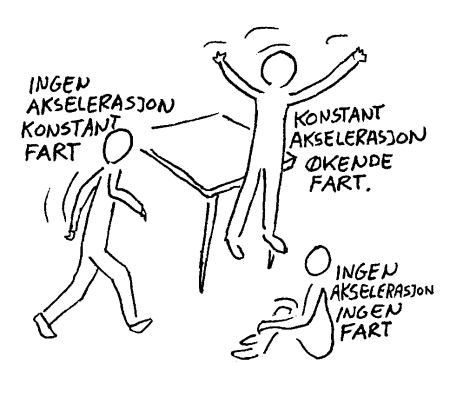
Disse formlene bør man huske. Om vi trenger andre formler vil vi her foreslå at man leter disse opp i bøker eller utleder disse fra de som er nevnt her.
Akselerasjon er et nyttig begrep som kan hjelpe oss med å finne svar på ulike praktiske spørsmål. Under følger noen nyttige formler i denne sammenhengen. Her vil vi anbefale at man ikke pugger disse, men merker seg hvor man kan slå dem opp.
v = v0 + at
s = (v0+v) * t / 2
s = v0t + ½ at²
v2 - v02 = 2as
Merk at vi her har fire begrep (s,t,v og a) og hver likning gir da en sammenheng mellom tre av disse. En av årsakene til at disse likningene er nyttige her på jorda, er at ting som faller fritt vil ha en fast akselerasjon på 9.8m/s² (~10m/s²). Dette gjelder om vi ser bort fra luftmotstanden som er liten når farten er liten.
Grafiske fremstillinger av bevegelser
Fart og akselerasjon kan defineres både med ord og med matematiske symboler. Nå finnes det en tredje måte å forklare hva vi mener med disse begrepene, som mange opplever som oppklarende. Denne metoden går ut på å lage grafiske kurver som viser hva vi mener med fart og akselerasjon. En kurve har to akser, og vi finner da tre vanlige sammensetninger av akser. X-aksen blir da vanligvis brukt til tida (t) mens y-aksen kan da vise avstand (s), fart (v) eller akselerasjon (a). Her følger en kommentar til hver av de tre typene av diagram.
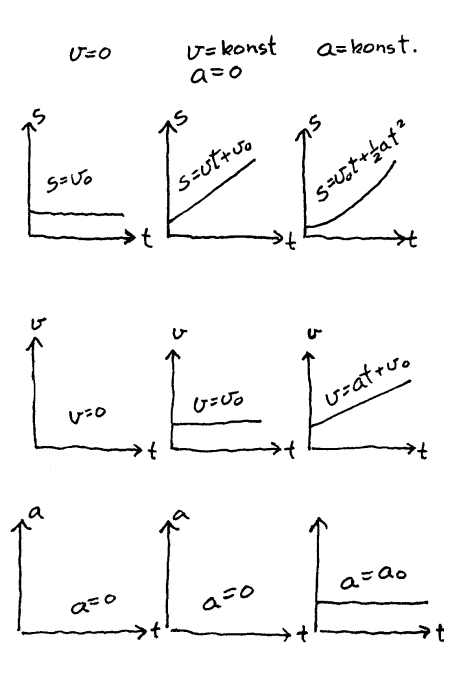
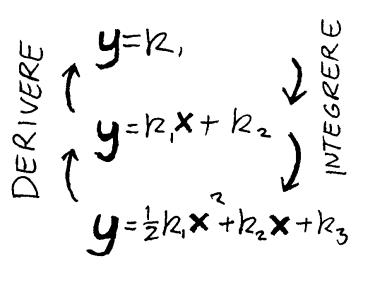
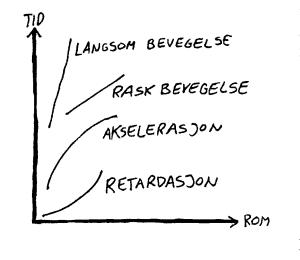
S-T-diagram: I dette diagrammet vil stillstand være ei vannrett linje (Tida vil alltid gå). Jevn hastighet vil fremstilles som ei rett linje og den blir brattere jo høgere hastigheten er. Akselererte bevegelser kjennetegnes av at kurvene avbøyes. Se figurer til venstre.
V-T-diagram: I dette diagrammet vil stillstand bli ei linje langs x-aksen. Jevn hastighet vil være ei vannrett linje. Jo høgere hastighet jo høgere opp blir linja. Akselerert bevegelser kjennetegnes i dette diagrammet av skrålinjer. Jo brattere kurver, jo mer akselerasjon. Se figurer til venstre.
A-T-diagram: I dette diagrammet vil stillstand og jevn hastighet bli ei linje på x-aksen. Jevn akselerasjon vil bli ei horisontal rett linje. Høyden til linjen vil da vise størrelsen til akselerasjonen. Se figurer til venstre.
Litt ekstra matematikk
Merk at vi også kan ha bevegelser med variabel akselerasjon, men da disse er så vanskelige å behandle matematisk blir de sjeldent omtalt i lærebøker.
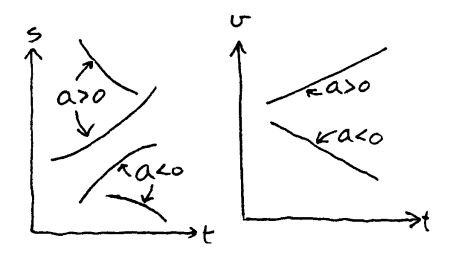
Akselerasjonen kan være positiv eller negativ. Positiv akselerasjon er en økning i hastigheten og tilsvarer det vi vanligvis forstår med akselerasjon. Negativ akselerasjon kalles ofte retardasjon og det får vi når farten avtar.
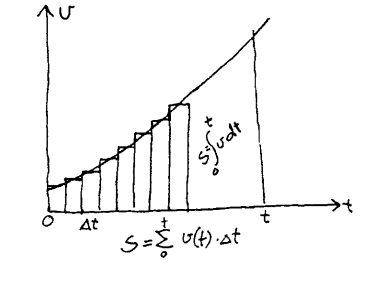
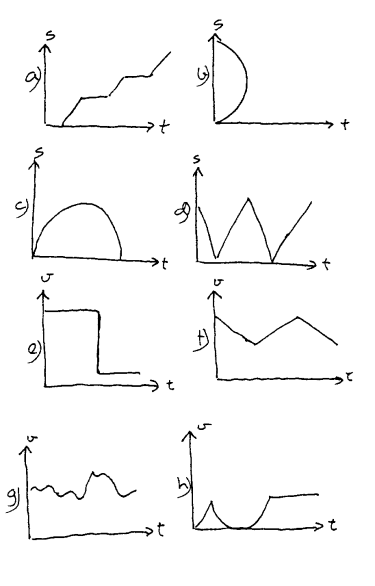
Merk også at det er et "mønster" i diagrammene ovenfor. Om vi starter ovenfra begynner vi f.eks. med en bøyd kurve. Så blir det en skråstilt rett linje, en horisontal rett linje og ei linje langs x-aksen til slutt. Hver av kurvene kan representeres av et matematisk uttrykk/likning som også er vist på figuren. Når vi deriverer ei likning tilsvarer det at vi forflytter oss ett hakk ned. Om vi integrerer ei likning tilsvarer det en forflytning ett hakk opp. I praktiske tilfeller kan vi derfor finne avstandslikning (s=f(t)), fartslikning (v=f(t)) eller akselerasjonslikning (a=(f(t)) ved å integrere eller derivere noen av de andre. Den grafiske fremstillingen er en hjelp til å forstå hva som skjer i disse matematiske metodene. Merk ellers at arealet under V-T-diagrammet tilsvarer s (avstand). Når en datamaskin finne s utfra likninga v=f(t), summerer den egentlig arealet av mange små søyler under kurven. Se figuren til venstre.
Oppgaver
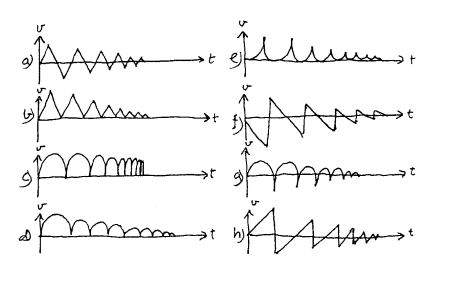
1 Hvilke bevegelser er mulig og hva skjer? (
figurer til høyre )
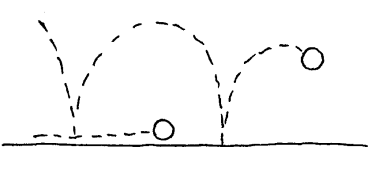
2 Hvilke av disse beskriver en bordtennisball som spretter på gulvet?(figurer under)

Newtons lover
Er Newtons lover for vanskelig for grunnskolen?
På slutten av 70 årene ble det i Norge gjort noen undersøkelser av hva som satt igjen etter at elever hadde lært Newtons mekanikk i skoleverket. Resultatene var ganske entydige. Et stort flertall hadde ikke fått med seg grunnidéene på en slik måte at de kunne anvende dem i praktiske situasjoner. Noen trakk da den konklusjonen at det er bortkastet tid å snakke om Newtons lover i grunnskolen. Resultatet er at vi i dag finner lite mekanikk i norske lærebøker. Her vil vi påstå at ovennevnte tolkninger og reaksjoner er uheldige. Det er ikke sikkert at det er mekanikken det er noe feil med. Et alternativ er å vurdere om mekanikkundervisningen kan bli bedre. Å si noe generelt om hvordan Newtons mekanikk undervises i grunnskolen er vanskelig. En måte å danne seg et bilde av undervisningen i grunnskolene, er å studere lærebøker som ble brukt. Om vi studerer de lærebøkene som ble brukt den gangen mekanikk fortsatt var "pensum", så var de relativt vanlig at elevene skulle eksperimentere seg fram til Newtons lover. Ved hjelp av utvalgte eksperiment hvor man varierte ytre betingelser på en strukturert måte, skulle elevene oppdage Newtons lover. Lærebøkene la opp til at elevene skulle praktisere vitenskapelige metoder og forventer at elevene skulle trekke konklusjoner de rette konklusjonene utfra hva de observerte.
Er dette den beste metoden for å lære mekanikk i norsk grunnskole? Det sentrale i Newtons mekanikk er loven ΣF=ma. Tilsvarende har vi U=RI i elektrisitetslæra og ΔU=Q+W i varmelæra. Tilsynelatende er disse svært enkle. Problemet med disse er ikke at sammenhengen mellom de enkelte begrepene er spesielt vanskelig. Når vi gjør forsøk og påviser denne sammenhengen, så er det vel grunn til å tro at elevene skjønner forsøkene. Problemet ligger vel heller i at selve begrepene er dårlig forstått, og at elevene ikke kjenner begrepene igjen i dagliglivet. Undervisningen vektlegger altså ikke å svare på problem som elevene har. I stedet tar undervisningen opp sammenheng mellom begrep som elevene oppfatter som fjerne. I tilfellet med ΣF=ma er alle begrepene vanskelige og litt fjerne fra dagliglivet. Et annet problem er at vi ofte bruker de samme lovene for å definerer de ulike begrepene. Formelen ovenfor kan f.eks. oppfattes som en kvalitativ forklaring på hva vi mener med en kraft eller en kvantitativ bestemmelse av hvor mye 1 kg er (m=ΣF/a).

Hverdagsforestillinger er et begrep som er knyttet til de forestillingene som elevene selv har utviklet. Elevene har ulike erfaringer som gjør at de kan forutsi hva som vil skje i mange vanlige situasjoner. I denne forbindelsen bruker de begrep som de vanligvis har hørt fra andre, men hvor de ofte selv har definert innholdet. En elev kan med andre ord ha en annen definisjon på ordet kraft enn den en fysiker har. Erfaringer fra skolen har vist at elevenes hverdagsforestillinger kan være et problem i møte med Newtons lover. Hvis elevene i fysikktimene får høre om noen såkalte naturlover, og får se mange uvanlige instrumenter, er det vel forståelig at elevene ikke kopler dette sammen med de hverdagsforestillingene han har fra før. Det betyr at både Newtons lover og hverdagsforestillingene får leve i fred side om side. Enkelte erfaringer vil kanskje utfordre feil hverdagsforestillingene, men uten systematisk veiledning vil nok hverdagsforestillingene overleve på lang sikt siden disse er basert på noe elevene opplever til daglig. Elevene vil ofte tenke at Newtons lover er noe som er aktuelt i forbinelse med prøver. Når så disse prøvene er unnagjort er det da liten grunn til å huske dem. Dette betyr at det er hverdagsforestillingene som overlever på lang sikt.



Generelle didaktiske tips
Utgangspunktet for dette heftet er at Newtons lover er rett, og hverdagsforestillinger som "kolliderer" med disse er feil. Bakgrunnen for å tro dette er da at Newtons lover ikke møter problem i forhold til virkeligheten, men hverdagsforestillinger vil derimot ofte få problemer med å forklare virkeligheten. Hvis vi ønsker å gjøre elevenes hverdag mindre problemfylt, kan det derfor være en idé å lære dem Newtons lover. Newtons lover er både generelle og abstrakte. De er derfor ikke så lett for elevene å få øye på dem i deres konkrete hverdag. Vi bør derfor bruke endel tid på å lede elevenes tanker inn i rette spor. Vanligvis vi det si at vi samtaler med elevene med utgangspunkt i ulike praktiske situasjoner.
Utstyr som brukes bør være mest mulig hentet fra elevenes hverdag for å unngå at elevene får en todelt virkelighetsforståelse. Det vil si at de beholder hverdagsforstillingene og lærer mekanikken som noe som bare gjelder i fysikktimene. Henter vi eksempler fra det som eleven omgir seg med til daglig, vil en bieffekt være at eksempelgjenstandene som brukes vil fungere som "tause påminnelser" om det som vi lærte i skolen.
Newtons mekanikk består av begrep og forklaringer som kan formuleres på en presis og rett måte. Legger vi for mye vekt på dette, vil det ofte virke hemmende på elevenes kreativitet og nytenkning i forhold til dette vanskelige emnet. Generelt bør vi akseptere mest mulig av de begrepsdefinisjonene og forklaringene som elevene gir. I tilfelle elevene har begrepsforståelser eller forklaringsmodeller som er direkte gale, og som vil hindre videre læring, bør endringen av disse skje mest mulig innenfor rammene av en veiledningssituasjon. Det vil si at veilederen gjennom spørsmål henleder elevens oppmerksomhet mot det som er problemet. Det er da et ønske om at eleven selv skal oppdage problemer i egne forestillinger, og så selv foreslår forbedringer.
Mekanikken gir mulighet for å illustrere hva vi mener med vitenskapelig arbeidsmåte og metode. Et kjennetegn på denne er at vi ikke trekker større konklusjoner enn det observasjonene tillater. Ofte må vi gjør mange systematiske forsøk som følger et bestemt mønster, for å komme fram til en konklusjon. På universitetsnivå er det nyttig at studentene får øving i vitenskapelige metoder. I grunnskolen er det fare for at elevene hverken lærer metoden eller fagstoffet om vi krever for mye av dem. Videre viser historien at de fleste av grunnleggerne av moderne vitenskap ikke fulgte de senere utviklede vitenskapelige metodene, men resultatene deres er ikke dårligere av den grunn. En elev står på mange måter i samme situasjon som Kepler og Newton. Både lovmessigheter, begrep og metoder er ukjent. I slike situasjoner er det viktig at elevene selv får være med å legge opp løpet.
Kjernen i Newtons lover
En av de største oppdagelsene i vitenskapens historie var Newton's oppdagelse av at noen enkle lover kunne forklare alt som skjer både på jorda og i universet når det gjelder bevegelser. Også i dag er disse lovene sentrale i mange sammenhenger. De er for eksempel grunnleggende når det gjelder navigasjon av moderne romfartøy. Nå er lovene matematiske i sin grunnform. I dette heftet vil vi legge vekt på å forklare med ord hva lovene egentlig sier. I det følgende vil vi derfor ta for oss Newtons 3 lover samt gravitasjonsloven som noen har kalt Newtons 4 lov og beskrive dem med ord. Generelt kan vi da si at Newtons lover forteller hvorfor gjenstander på jorda og i universet oppfører seg slik de gjør.

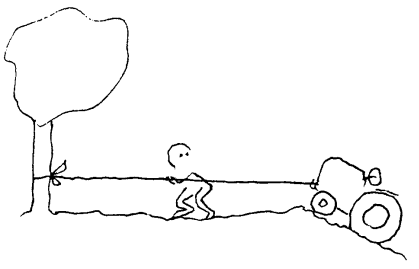
Summen av alle kreftene på tauet kaller vi kraftsum. Om kraftsummen er forskjellig fra 0 vil ett av lagene vinne
Newtons første lov
Denne loven forteller om en enkel sammenheng mellom kreftene som virker på et legeme og bevegelsene til legemet. Om vi f.eks. tenker oss to lag som trekker i et tau, så vet alle at det laget vinner som klarer mobilisere den største kraften på tauet. Et lag har vunnet når det andre laget er trukket over ei bestemt linje. Det er altså en sammenheng mellom krefter og hvor lagene befinner seg i forhold til linja. Nå kan vi tenke oss at det f.eks. er 2, 5 eller 10 personer på hver side av tauet. Jo flere personer som er involvert, jo større krefter er det snakk om. Men i denne situasjonen er det ikke størrelsen på de kreftene som lagene produserer, som er avgjørende, men forskjellen mellom kreftene. Klarer f.eks. det ene laget å dra i tauet med en kraft som er 1 N sterke enn det andre laget klarer, vil de vinne. Det avgjørende er altså ikke enkeltkrefter, men en ubalanse mellom kreftene som avgjør bevegelsen til de to lagene.
Fordi vi har definert krefter som vektorer, vil den ubalansen i krefter som er nevnt ovenfor, fremkomme når vi summerer alle kreftene som virker fra de enkelte deltakerne. Det er denne kraftsummen som Newtons lov handler om. Derfor bruker vi vanligvis tegnet Σ foran F. ΣF kan da leses som 'summen av kreftene'. Et problem i forbindelse med Newtons lover, er vel at vi glemmer noen krefter, og det vi tror er kraftsummen er da ikke den virkelige kraftsummen.
Det normale blir ikke kommentert
Newtons første lov sier da noe om hva slags bevegelser de ulike legemene får. Måten vi her beskriver det som skjer omkring oss illustrerer et grunnleggende poeng når det gjelder vår tanke om naturen. Følgende to utsagn illustrerer dette:
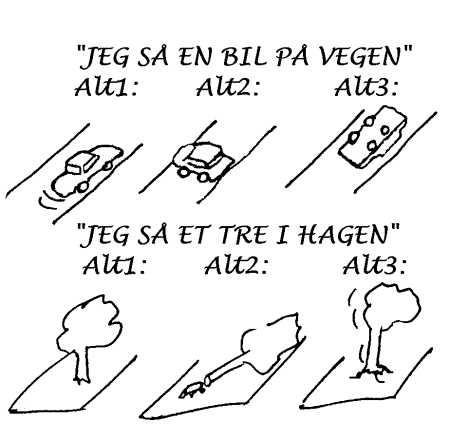
Jeg så en bil på vegen
Det var et tre i hagen
Når vi ser/hører utsagn som disse vil vi automatisk legge til visse tanker. Dermed vil vi få mer ut av setningene enn det som direkte står i setningene. Dette kommer av at vi oppfatter noe som normalt eller underforstått. Dette er da tilfelle om ikke annet er uttrykkelig beskrevet. I tilfellet ovenfor vil nok de fleste regne med at bilen kjørte og treet stod stille i oppreist stilling. Dette fordi det er det vi vanligvis ser på veger og i villahager. Om bilen stod stille midt på vegen ville det sannsynligvis vært kommentert. Tilsvarende ville vi nevnt noe om det hvis treet lå på bakken eller beveget seg rundt i haven. Vi tar med andre ord noe for gitt. Når vi i fysikktimene beskriver noe, bør vi være oppmerksom på at elevene ofte "tilføyer" ting som vi ikke har sagt.
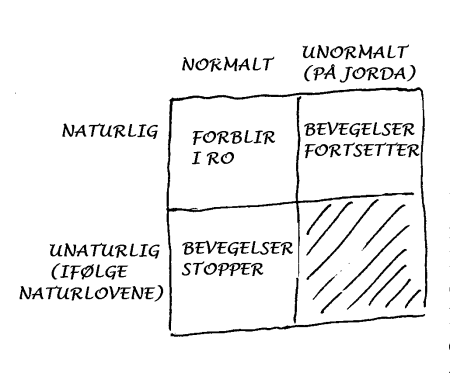
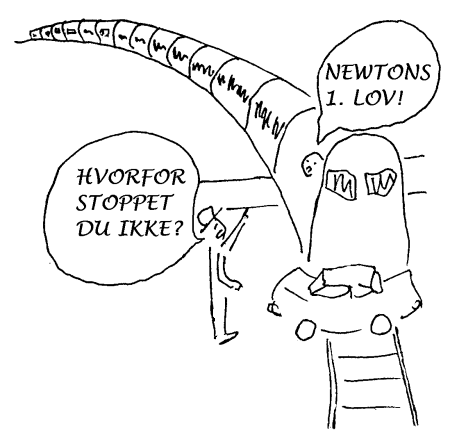
Generelt kan vi si at vi vanligvis kommenterer det unormale. I mekanikken har vi et problem. Når vi skal forklare det som skjer i naturen, blir det mest oversiktlig om vi først gjør oss kjent med de reglene eller lovene som gjelder. Siden kan vi så konsentrere oss om å forklare de tilfellene hvor lovene eller reglene tilsynelatende blir brutt. Dette er ikke så enkelt i mekanikken. Hovedproblemet er at vi vanligvis opplever unntakene fra regelen og ikke regelen selv. Dette skal vi prøve å illustrere i det følgende. Først vil vi reservere ordene NORMAL og NATURLIG slik at de brukes konsekvent om to ulike ting. Ordet normal skal da brukes om det vi opplever her på jorda, mens ordet naturlig i det følgende brukes om det som følger Newtons lover.
Problemet med Newtons første lov da at den er naturlig, men ikke nødvendigvis normal. Vi opplever altså sjeldent "naturlige" bevegelser til legemer i våre nære omgivelser. Det normale er ofte ikke naturlig eller omvendt. Hva er så ifølge Newtons første lov naturlig bevegelse til et legeme? Vi bruker ofte begrepet bevegelsestilstand når vi snakker om dette. Newtons første lov sier at det naturlige for et legeme er å ikke endre bevegelsestilstand. Det naturlige er altså uforandret bevegelsestilstand. Isolert sett vil vi da si at det er unaturlig for et legeme å forandre bevegelsestilstand. Det er imidlertid mulig for et legeme å forandre bevegelsestilstand, men da vil det alltid skje som følge av at det virker en kraft på legemet.
Før vi ser nærmere på anvendelser av loven i konkrete situasjoner, må vi definere hva vi mener med bevegelsestilstand. Ifølge Newton kan et legeme være i ro. Dette er da en bevegelsestilstand som legemet kan fortsette å ha inntil krefter kommer å forstyrrer. Dette er det vi alle opplever daglig. Det er derfor ikke noe vanskelig å akseptere at det naturlige for legemet å fortsatt være i ro. Det er også normalt. Problemene oppstår når vi studerer legemer som beveger seg. Da sier Newtons første lov at det er naturlig at bevegelsene fortsetter med jevn fart i samme retning uten stopp. Dette opplever vi ikke til vanlig, og derfor vil vi karakterisere det som unormalt her på jorda. Men siden Newtons lover gjelder både på jorda og i universet, så er det mulig å tenke seg steder hvor legemer fortsetter å bevege seg med jevn fart og retning "til evig tid". Dette er da naturlige for alle gjenstander i universet. Det er derfor unødvendig å forklare hvorfor bevegelsene fortsetter. Det er bare sånn. Hvis derimot en gjenstand som er satt i bevegelse stopper slik de alltid gjør her på jorda, er det nødvendig med en forklaring!

Hvorfor?
Nå er det ikke så vanskelig å forklare hvorfor ting stopper her på jorda. To stikkord i denne sammenhengen er friksjonskraft og gravitasjonskraft. Nå er disse kreftene i seg sjøl naturlige krefter, og det kan virke forvirrende å si at det er unaturlig når ting stopper her på jorda. Det vi må fastholde i denne forklaringen, er at det er unaturlig for en gjenstand isolert sett å stoppe etter at den er satt i bevegelse. Siden ingen gjenstander her på jorda kan isoleres fullstendig fra påvirkning fra omgivelsene, vil vi få at "alt på jorda stopper". Dette er normalt men ikke nødvendigvis naturlig. Det finnes alltid en årsak til at ting stopper og derfor kan vi alltid si at det stoppet på grunn av den eller den kraften.
Et eksempel: På ei plan isflate vil friksjonen være forholdsvis liten. Vi vil kunne oppleve at en skøyteløper vil kunne bevege seg ganske langt med tilnærmet samme fart og samme retning uten å gjøre noe for det selv. I dette tilfelle blir da ikke utfordringen å forklare hvorfor han beveget seg så langt. Det er altså naturlig for skøyteløperen å fortsette når han først har fått fart. Derimot bør vi heller forklare hvorfor han stoppet til slutt. Årsaken til det er da friksjon. Om noen synes det er unormalt å gli så langt før vi stopper, så er det en måte å se det på som vi bør akseptere. Men om vi skal snu på forklaringen og forklare hva som gjør at skøyteløperen glir så langt blir forklaringen straks mye mer komplisert. Treghet og glatt is/liten friksjon er aktuelle begrep, men disse "tilfører ikke skøyteløperen noe" som forklarer hvorfor skøyteløperen glir så langt. Da Newton formulerte lovene sine, var ikke grunnen at han ville gjøre det vanskeligere å forstå og forklare det som skjer rundt oss, men omvendt. Han ville hjelpe oss, og her vil vi påstå at livet blir enklere om vi forstår Newtons lover.
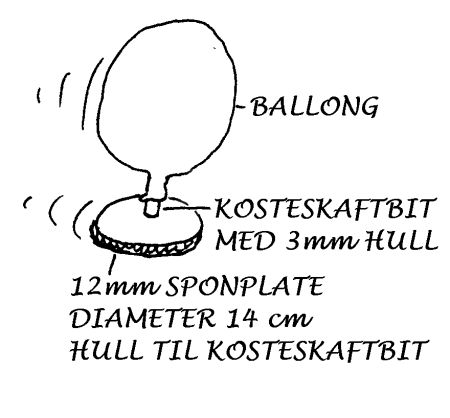
Demonstrasjonseksempler Legger vi en tennisball et eller annet sted vil den bli liggende. Bevegelsestilstanden endres altså ikke før vi igjen påvirker den med krefter. Så langt er det ikke vanskelig å akseptere Newtons første lov. Det normale samsvarer her med det naturlige. Kaster vi derimot tennisballen i klasserommet vil vi se at den langt fra har noen rettlinjet bevegelse med jevn hastighet. Hvis vi skal ha sjanse til å overbevise elevene om at Newtons første lov fortsatt gjelder, må vi da sikre at de "ser" at det er krefter som forstyrrer ballens naturlige bevegelser. Hvilke krefter er det og hvordan påvirker de ballens bevegelser? Om vi triller tennisballen på gulvet, kan vi "eliminere" gravitasjonskraften (fordi normalkraft vil motvirke tyngdekraft). Men fortsatt vil friksjonskraften virke relativt sterkt. Om vi så samtidig triller ei klinkekule og en tennisball burde det være mulig å få elevene til å konkludere med at form (størrelse) og masse til kulene betyr noe for hvor langt kulene tiller. Jo lenger de trille jo mindre betyr de forstyrrende kreftene og jo nærmere kommer vi en "naturlig" situasjon. For å minimalisere friksjonskreftene finnes ulike teknikker. Det mest effektive er det såkalte luftputeprinsippet. Det kan vi demonstrere ved hjelp av et hjemmelaget luftputefartøy. Se figur.


Forskjell på Newton og Aristoteles
Når denne "treghetsloven" først ble formulert av Newton, så skyldes ikke det at mennesker ikke hadde vært opptatt av dette problemet før. Årsaken var vel heller at det ikke var noen før ham som hadde sett denne "enkle" loven. Et legeme kan generelt ha tre forskjellige typer bevegelsestilstander:
1) i ro
2) jevn fart
3) akselerasjon
I dagliglivet skiller vi vanligvis mellom ting som er i ro og ting som beveger seg. Vi bryr oss altså ikke om hva slags bevegelse det gjelder. Det gjorde også Aristoteles. Han mente da at det normale for et legeme var å være i ro. Videre observerte han tyngdekraftens virkning og la til at den normale plasseringen for legemene var lengst mulig nede. Alle unntak fra denne lovmessigheten skyldtes da ulike typer krefter ifølge Aristoteles. Newton's store oppdagelse bestod da i å flytte skillet mellom det naturlige og det som måtte forklares fra mellom 1) og 2) til mellom 2) og 3).
Oppgave Forklar bevegelsene til ei kjerre som trekkes av en okse og bevegelsene til ei pil utfra Newtons og Aristoteles modell. Husk at det er det "unormale" som må forklares.
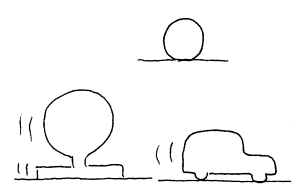

Oppsummering
Newtons 1.lov sier at en masse ikke vil forandre bevegelsestilstand (hastighet) hvis det ikke virker en kraft på massen. Jevn hastighet er med andre ord det naturlige for alle legemer/masser. Hvis det da bare fantes ett legeme i universet ville det fortsette med uforandret hastighet i uendelige tider uten at det hadde noen mulighet til å forandre på dette. Nå er det imidlertid slik at masser i universet tiltrekker hverandre (gravitasjon), og ingen masser vil derfor være upåvirket av krefter. Det betyr at vi aldri vil oppleve at masser oppfører seg 100% som beskrevet ovenfor. Newtons første lov gjelder også hvis summen av kreftene på en masse er lik null. Her på jorda vil vi bare kunne skape tilstander hvor denne betingelsen er nesten oppfylt. Før eller siden vil friksjonskrefter stoppe alle bevegelser på jorda. Friksjon er den kraften som motvirker en bevegelse. Newton's første lov er ellers et spesialtilfelle av Newton's andre lov. Når vi har brukt mye tid på denne første loven, så har det først og fremst pedagogiske årsaker.
Oppgaver
1 Ingen akselerasjon (a=0) betyr at summen av kreftene på dem er lik null. Tegn krefter på steinen i ro og luftputefartøyet og bilen i jevn fart.

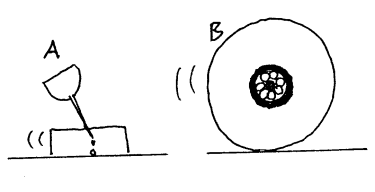
2 Liten friksjon betyr ofte tilnærmet jevn hastighet. Olje, hjul med kulelager, is, vann og luft gir alle relativt liten friksjon. I mange tilfeller er nettopp minst mulig friksjon et mål for teknologene. Ranger figurene A-E i forhold til størrelsen til friksjonen.
Newtons andre lov
Denne loven er mest kjent, og den sier kort at kraft er lik masse ganger med akselerasjon.
SF = ma
På ikke-matematisk form kan vi si at alle legemer som blir utsatt for en kraftsum som er forskjellig fra null, vil få en akselerasjon som er stor når kraftsummen er stor og massen er liten. Videre vil kraftsummen og akselerasjonen alltid ha samme retning. Når tre begrep er knyttet sammen på en slik måte, kan det være vanskelig å forstå sammenhengene utfra bare formelen. Vi vil derfor kort beskrive noen situasjoner hvor vi holder en og en av disse begrepene noenlunde konstant, og så varierer de andre.
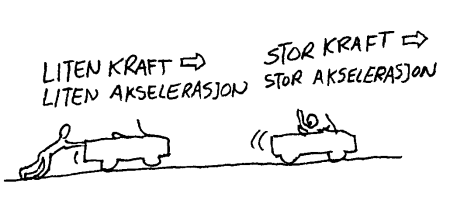
Konstant masse
Om en personer skyver på en bil, vil det være grense for hvor mye farten til bilen kan økes på ei slett strekning. Om vi derimot kopler inn motoren som kan yte langt større krefter, vil vi se tydelig forskjell på akselerasjonen. Om vi måler ulik akselerasjon på en bil i to ulike tilfeller, så skyldes det at kreftene var ulike i de to tilfellene. Hvis vi i et tilfelle har dobbelt akselerasjon har det sin årsak i en kraftsum som er dobbelt så stor. Nevn andre eksempler som illustrerer sammenhengen mellom kraft og akselerasjon når massen er fast.

Konstant kraft
Om vi kaster en lett ball og ei tung kule så langt vi kan, vil vi oppleve at den lette ballen får størst fart i starten. Det betyr at vi klarte å gi den lette ballen størst akselerasjon mens den var i handa. Masse og akselerasjon er her omvendt proporsjonale. Når den ene øker så vil den andre avta i verdi. Et togsett som starter vil ha relativt liten akselerasjon. Grunnen er at togsettet har stor masse. Et enkelt lokomotiv vil kunne ha større akselerasjon siden massen er mindre. Nevn andre eksempler som illustrerer sammenhengen mellom masse og akselerasjon.
Konstant akselerasjon
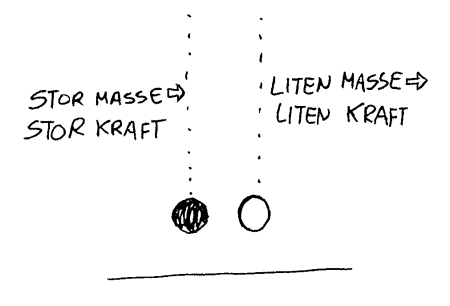
Vi kan tenke oss at en stor og en liten person oppnår sammen akselerasjon i et spurtoppgjør. Massen til personene vil være ulik. Når akselerasjonen likevel er lik, så må det skyldes at den store personen klarte å mobilisere større krefter enn personen med mindre masse. Om vi slipper ei blykule og ei trekule vil de nå gulvet omtrent samtidig. Det vil si at de hadde omtrent samme akselerasjon. På blykula vil det virke en større kraft enn på trekula. På den andre siden vil det kreves større kraft for å akselerere en gjenstand med stor masse. Fortrinnet med stor kraft blir altså opphevet av ulempen med stor masse, og resultatet blir lik akselerasjon. Nevn andre eksempler som illustrerer sammenhengen mellom kraft og masse.
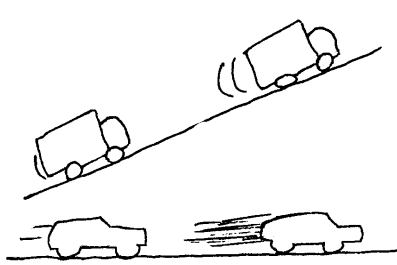
Stor kraft =>Stor fart i bakker (fordi man kan bruke høyere gear, eller fordi stor kraft gir stor effekt=arbeid/tid)
Stor kraft => Stor toppfart (fordi luftmotstanden øker ved høye hastigheter)
..men direkte kobling finnes bare mellom kraft og akselerasjon
Treg masse
Det som er nevnt ovenfor viser at motstanden mot å bli akselerert øker når massen øker. Motstanden mot å bli akselerert kalles ofte treghet. Her er det massen til et legeme som bestemmer tregheten. Formelen ovenfor gir sammenhengen mellom masse og treghet. Vi kan med andre ord si at formelen ovenfor definerer treg masse. Treg masse er definert som forholdet mellom kraftsummen og akselerasjonen til et legeme. (m= SF/a) Vi har til nå betraktet masse-begrepet som et grunnbegrep som er kjent og enkelt å lære. Jo mer vi studerer massebegrepet, jo mer oppdager vi at dette ikke er et enkelt begrep. Den egenskapen ved et legeme som vi kaller masse, viser seg på den ene siden som en motstand mot akselerasjon. Da kan vi bruke formelen ovenfor for å beregne massen. Fordi det er vanskelig å beregne både kraft og akselerasjon til noe som beveger seg, er det vanlig å bruke en annen metode for å beregne massen. Den andre måten å beregne massen til en gjenstand har sammenheng med at masser vil oppleve en kraft i et tyngdefelt eller et gravitasjonsfelt. Når vi beregner massen til et legeme med ei vekt finner vi egentlig det vi kan kalle gravitasjonsmasse. Teoretisk sett kan treg masse og gravitasjonsmasse være to ulike ting, men i praksis antar vi at det er samme massen det dreier seg om. Alle forsøk tyder på det.
Undervisning i skolen
Til forskjell fra endel lærebøker som behandler Newtons andre lov, har vi ikke gjort noen forsøk på vise til eksperiment som bekrefter lovmessigheten ovenfor. De aktuelle eksperimentene er fysisk sett enkle nok. Men det er ikke enkelt å trekke konklusjoner utfra eksperimentene, og følgelig er de kanskje ikke spesielt nyttige i grunnskolen. Her har vi vektlagt at elevene skal forstå at det er en sammenheng mellom akselerasjon, kraftsum og masse. Når vi snakker om biler med mange hestekrefter (F) under panseret så er det samtidig vanlig å nevne noe om toppfart (v). Også på idrettsarenaer og andre steder har vi lett for å kople sammen krefter med fart. Jo større krefter jo større blir farten. Utfra Newtons andre lov er det en kopling mellom kraft og akselerasjon og ikke en kopling mellom kraft og fart. Et mål i skolen er derfor å erstattet koplingen til fart med en kopling til akselerasjon hos elevene. Hvis vi ikke klarer dette, vil den oppvoksende slekt forblir i en "før-newtonsk verdensforståelse". Nå vil nok enkeltpersoner klare seg godt uten Newtons verdensforståelse, men om dette blir det normale i et samfunn som nettopp har bygd velstanden på denne forståelsen, så står kanskje velstandsamfunnet vårt i fare.
Når det påviselig er en sammenheng mellom toppfart og krefter i ulike situasjoner, så skyldes det at ulike typer friksjonskrefter som luftmotstand ol. øker med hastigheten. Når vi nærmer oss toppfart, blir disse faktorene avgjørende. I en undervisningssituasjon bør vi si at det er en sammenheng mellom krefter og akselerasjon. Men vi må også opplyse om at det i mange praktiske situasjoner vil være en sammenheng mellom fart og kraft.
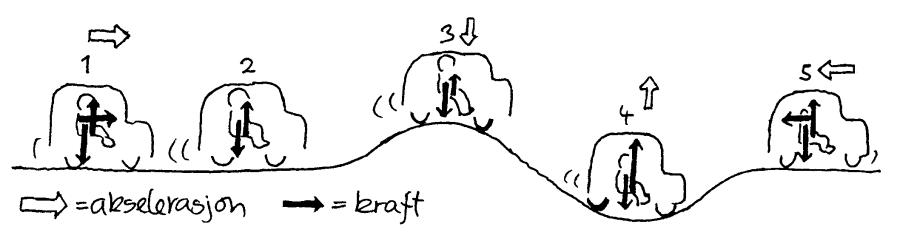

Newtons andre lov i praksis
Nå kan det være nyttig å tenke litt gjennom hva begrepene i denne andre loven egentlig står for, og hvordan vi kan måle dem. Kraft er et begrep som vi alle føler på kroppen i dagliglivet. Begrepet kraft krever vanligvis ikke noen nærmere forklaring. Derimot kan det være nødvendig å forklare hva som menes med kraftsum. I figuren nedenfor ser vi en bil som akselererer(1), kjører med jevn hastighet på ei slette(2), over en bakketopp(3), i en dump(4) samt bremser ned(5). Her har vi vist akselerasjonen og kraftsummen med piler i alle 5 tilfellene. I tilfellet ovenfor er farten framover. Akselerasjonen derimot bestemmes av hvilke retning kraftsummen er. Akselerasjonen er uavhengig av hastigheten, og derfor kan f.eks. akselerasjon og fart ha motsatt retning.
Oppgaver
1 Tegn på akselerasjonen til personen i heisen når heisen starter oppe (1) når heisen har jevn hastighet nedover (2) og når heisen stopper nede(3).
2 Nå er det vanskelig å måle både kraftsum og akselerasjon i praktiske eksempler. Disse må da oftest beregnes på en indirekte måte. Massen derimot er det lett å måle. Benevningen kg er vanlig i dagliglivet og de fleste vekter vil gi resultatet i kg. Siden massen er knyttet til selve legemet vil den ikke forandres. En kg sukker forblir en kg sukker om vi tar den med til månen, ut i universet eller inn i en sentrifuge. Hvor er kreftene størst på pakken med 1 kg sukker i figurene her?
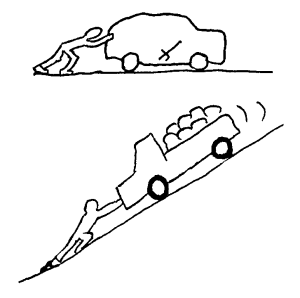
3 Merk at krefter ikke alltid vil medfører akselerasjon. Betingelsen for å få akselerasjon er at kraftsummen er forskjellig fra null. Ofte må vi overvinne friksjonskrefter for å få til akselerasjon. Noen ganger er andre krefter sterkere hindrer oss i å flytte på gjenstander. Om vi skyver på en bil med håndbremsen på vil vi vanligvis ikke kunne flytte den. Om vi skyver en bil oppover en bakke, kan vi oppleve at den totale bevegelsen er motsatt av den vi ønsker. Hvorfor får ikke kreftene fra mannen den vanlige virkningen i figurene til venstre?

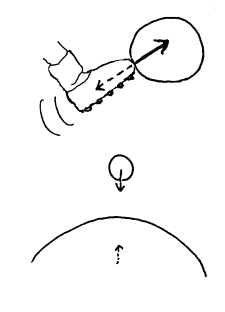
Newtons tredje lov
Samfunnet - et speilbilde av naturen?
To elever kan støte sammen i en gymtime ved et uhell. Kanskje setter de seg begge setter seg ned og gråter. Kanskje opplever begge at det var den andres feil. Liksom det i samfunnet må være minst to for å få i stand en konflikt, må det i naturen være minst to for å skape en kraft. Krefter kan deformere ting, og om kreftene blir for sterke vil vi mennesker oftest oppleve virkningen som smertefull. I eksempelet hvor to elever støter sammen, kan kanskje Newtons tredje lov være aktuell for å avlede oppmerksomheten fra det vonde både når det gjelder fysiske smerter og psykiske trusler. I idrettsleker lages lover/regler for å hindre at noen skal få urettmessige fordeler eller skades. I hvor stor grad disse holdes er avhengig av mange faktorer. I naturen finnes det også lover. I motsetning til menneskeskapte lover vil naturens lover alltid gjelde, og de vil alltid virke rettferdig. Det rettferdige i situasjonen ovenfor er da at de kreftene de to elevene opplevde var akkurat like store. Også når vi sloss vil de kreftene som virker mellom partene alltid være like store. En teknikk i en slåsskamp er å treffe motstanderen med slag på steder som er mer følsomt for slag enn det handa er. Kraften fra handa til magen er like stor som kraften fra magen til handa, men den føles nok verst i magen.
Generelt om Newtons tredje lov
Newtons 3.lov sier at det til enhver kraft vil være en motkraft som er like stor og motsatt rettet. Disse kreftene virker på hvert sitt legeme. Dette kan illustreres hvis vi tenker på et ballspark. Det vil her være en kraft fra foten som akselererer ballen ifølge Newtons andre lov. Samtidig vil det være en kraft fra ballen på foten som gir denne negativ akselerasjon (retardasjon). At dette er en virkelig kraft, kan vi lettest erfare hvis vi sparker hardt på en ball uten at vi har sko på foten.
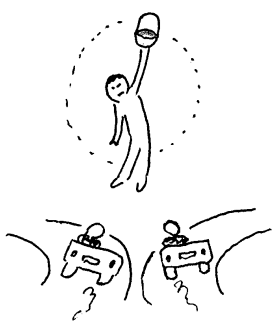
Hva er det her som ikke har motkrefter og som dermed ikke er ekte krefter
Alle krefter har en motkraft
Ved nærkrefter virker kraft og motkraft i samme punkt. Når det gjelder fjernkrefter som tyngdekraften er et eksempel på, et det ofte litt verre å oppdage motkraften. Motkraften til den gravitasjonskraften som trekker en stein mot jorda, er da en kraft som trekker jorda mot steinen.
Merk at alle ekte krefter har en motkraft. Dette er derfor en test på om vi har med en ekte kraft å gjøre. I endel situasjoner kan vi "føle" krefter, som følge av at vi blir akselerert. I disse tilfellene er det egentlig massens uvilje mot å bli akselerert, som vi føler og ofte kaller vi disse kreftene for treghetskrefter. Dette kan vi demonstrere ved å dreier ei bøtte med vann i. Gjør vi dette fort nok vil ikke vannet renne ut selv om bøtta "står på hode". Vannet føler med andre ord en kraft som trekker det oppover i bøtta som er sterkere enn gravitasjonskraften som trekker det ned. Den kraften som drar vannet opp i bøtta er da en uekte kraft. Denne kraften finnes da bare om vi ser det hele fra "bøttas synsvinkel". Fra et ikke-akselerert synspunkt vil vi imidlertid si at de kreftene som virker på vannet i bøtta, er gravitasjonskraften og en mindre kraft fra bunnen i bøtta, begge med retning nedover. Disse virker altså i samme retning og medfører at vannet faller eller har en akselerasjon (sirkelbevegelse) slik Newtons andre lov forteller. Han som holder i bøtta vil imidlertid akselerere bøtta like mye slik at den hele tida omslutter vannet. Et annet eksempel er de kreftene vi føler når bilen kjører i svinger. Disse kreftene kalles ofte sentrifugalkrefter. De har ikke motkrefter, og er derfor ikke virkelige krefter. Det er viktig at de ikke tegnes opp som vanlige krefter. Vi vil komme tilbake til flere eksempler når vi senere skal prøve å forklare flo og fjære og lavtrykk/høytrykk (corioliskraften).
Gravitasjonsloven (Newtons 4. lov)
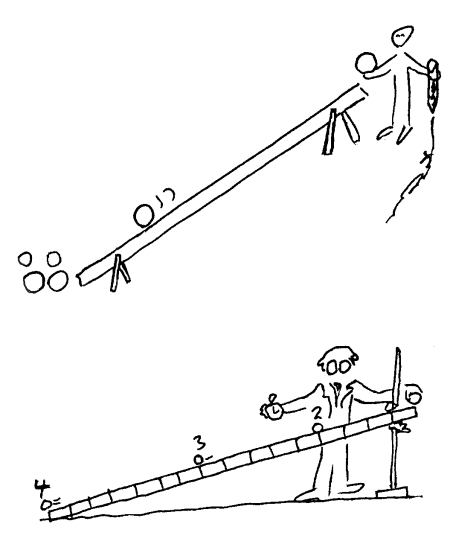
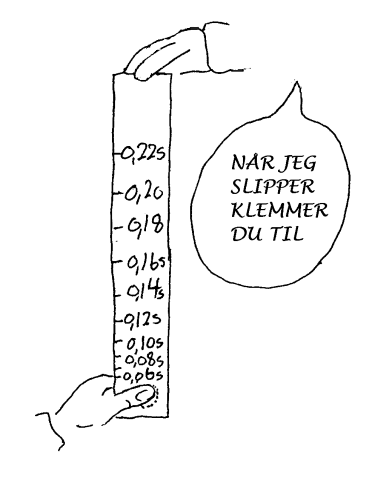
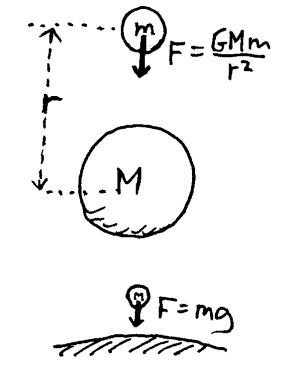
Galileo's forsøk
De tre lovene vi har sett på til nå, er kanskje ikke så vanskelige i seg selv. Kanskje er de heller ikke så nyttige isolert sett. Her vil vi se litt nærmere på det vi til nå bare har nevnt som en av de mange kreftene som kan påvirke et legeme, nemlig gravitasjonskraften. På en måter kan vi si at det er denne kraften som gjør det vanskelig å finne Newtons lover i naturen. Sett utenfra var det vel ikke så komplisert det Galileo drev på med. Ifølge noen bøker slapp han ei jernkule og ei trekule fra toppen av det skjeve tårn i Pisa og observerte at det nådde bakken samtidig. Nå er det tvilsomt om han gjorde dette og om han gjorde det er det tvilsomt om kulene nådde bakken samtidig, men dette er da en populære fremstillingen av det han gjorde. Det vi med sikkerhet vet, er at han rullet ulike kuler langs skråplan med ulik helling. Han var opprinnelig opptatt av hva som skjedde med ting som falt fritt, men siden han ikke hadde tilgang på nøyaktige nok klokker og sensorer, trillet han heller kuler langs et skråplan for at eksperimentene skulle ta litt lengere tid. Klokken han brukte var basert på at vann renner med noenlunde jevn fart ut av et hull i en beholder. Skråplanet han brukte var ca. 6 meter langt.
Demonstrasjonsforsøk Vi kan gjøre forsøk som svarer til de eksperimentene Galilei gjorde. Vi kan f.eks. trille klinkekuler på skråplan som vi selv lager. Skal vi lage et skråplan som kan brukes til demonstrasjon, kan det være nyttig å la det være 16 enheter (dm) langt. Gjør vi helningen slik at kulen triller 16 enheter på 4 sekunder vil den da trille 9 enheter på 3 sekunder osv.
Generelt om gravitasjonsloven
Når det gjelder gravitasjonsloven som Newton har fått æren for, så kan vi si at det var Galilei som gjorde mye av grunnarbeidet for å komme fram til den. Det var imidlertid Newton som først formulerte den slik vi kjenner den i dag, og derfor er hans navn knyttet til denne loven. Ved hjelp av Newtons lover kan vi forklare alle bevegelser på jorda og i universet. Hva sier så gravitasjonsloven. I populærfremstillinger blir det ofte sagt at Newton oppdaget gravitasjonskraften/tyngdekraften da han fikk et eple i hode. Dette er misvisende. Selve gravitasjonskraften har alltid vært kjent. Det store med Newtons oppdagelse var at han klarte å lage et matematisk uttrykk for denne som gjaldt både på jorda og i universet. Det matematiske uttrykket er:
F = GMm/r² (generelt)
F = gm (ved jordoverflata)
G = 6,672*10-11 Nm²/kg² (gravitasjonskonstanten)
g = 9,8 m/s² (tyngdens akselerasjon/feltstyrken)
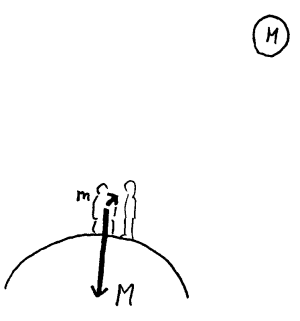
Disse forteller at det alltid virker en kraft mellom to masser, og at denne kraften er proporsjonal med størrelsen på hver av massene og omvendt proporsjonal med kvadratet av avstanden mellom massene. Enklere kan vi si at kraften mellom to masser øker når massene øker og minker når avstanden mellom dem øker. Verdien G er en konstant som trenges for at både tallverdiene og benevningene skal stemme overens på begge sidene av likhetstegnet. Den kalles gravitasjonskonstanten. (Her vil vi kort nevne at man har satt ulike spørsmålstegn ved denne lovmessigheten siden Newton først foreslo den. I ekstreme tilfeller har den da blitt avløst av Einsteins relativitetsteori, og noen har også satt et spørsmålstegn med om r-en skal opphøyes i 2 eller 3. Her vil vi ikke diskutere dette nærmere, men bare konkludere med at man i en undervisningssammenheng ikke bør være for bastand når det gjelder slike lover som fortsatt er gjenstand for diskusjoner.)
Vi representerer selv en masse på ca. 75 kg, og derfor vil andre masser omkring oss trekke på oss. Gravitasjonskraften fra jorda er mest kjent, men også månen vil trekke litt på oss. Når månen befinner seg rett over oss er det flo/høyvann, og i prinsippet skulle vi føle oss litt lettere. Fordi månen har mye mindre massen enn jorda og dessuten er mye lenger borte er kraften på oss fra månen ikke merkbar.
Oppgave Bruk formelen ovenfor og beregn gravitasjonskraften mellom to mennesker på 75 kg som har en avstand på 1 meter. Tror du at det er mulig å måle denne kraften? Finn også kraften fra månen på et menneske.

Gravitasjonsmasse
Om vi løfter på ulike steiner vil vi oppleve at de har ulik tyngde. Tyngden er da kraften som vi føler at steinene trekkes mot jorden med. Siden ulike steinene gir ulik kraft, kan vi konkludere med at steiner har et kjennetegn som kan variere. Dette kjennetegnet kaller vi masse. Vi antar videre at massen er proporsjonal med den kraften vi opplever. Dette er ikke så unaturlig fordi to like steiner vil føles dobbelt så tunge som en stein. Vi får så følgende sammenheng mellom kraft og masse:
F=mg
g er en eller annen konstant som vi i teorien kan velge fritt. Nå er det imidlertid slik at vi er blitt enig om kilogram (kg) som enhet for masse og newton (N) som enhet for kraft. En kg er definert som vekten av en prototyp i Frankrike. En N er definert som den kraften som får 1 kg til å akselerere 1 m/s². Den siste definisjonen bruker definisjonen av treg masse som er nevnt tidligere. Om vi bruke disse enhetene i den ovennevnte sammenhengen mellom kraft og masse vil konstanten vår få en bestemt verdi. Denne kan vi så finne utfra praktiske forsøk. Hvordan kan vi finne denne verdien om vi har en kraftmåler og ei vekt som gir oss massen? (g=F/m)

Forvirrende?
Om vi ser litt nøyere på sammenhengen mellom gravitasjonskraft og masse ovenfor, vil vi se at den likner på Newtons andre lov. Erstatter vi g med a og antar at gravitasjonsloven er den eneste kraften som virker, får vi nettopp Newtons andre lov. Men det var da ikke Newtons andre lov vi skulle fram til? Hvorfor får vi da samme formelen? Hva er så forskjellen på disse to lovene? Merk at slike "sammentreff" kan skape forvirring, og den aktuelle forvirringen er vel et eksempel på hovedproblemet for dem som skal forstå Newtons lover. Det er på en måte slik at alt starter og ender med en enkel formel. Det er ikke selve formelen som er problemet, men hva som er start og hva som er slutt. Hva vet vi og hva vet vi ikke? Generelt kan vi si at akselerasjon er et begrep som har sin definisjon utenfor formelen her, og derfor kan vi vel si at det er det mest grunnleggende begrepet. Videre har vi målt akselerasjonen til alt som faller ved jordoverflata til å være 9,8m/s². Tyngdens akselerasjon (g) kan vi da betrakte som en verdi som baserer seg på eksperimenter. Det var dette Galileo kom fram til, og det er en grunnleggende oppdagelsene i mekanikken. De to andre begrepene (F og m) er da mer diffuse. Generelt kan vi vel si at begge begrepene er definert gjennom Newtons andre lov. Dette er da vel strengt tatt den logiske årsaken til at Newtons andre lov er rett. Det er da massen til den internasjonale kilogramprototypen i Frankrike som gir oss et grunnlag for å gi begge begrepene en tallverdi. Newton måtte med andre ord lage seg to begrep som er uttrykk (masse og kraft) for det samme (i og med at de er proposjonale), og følgelig vil vi få problemer hver gang vi prøver å lage en logisk argumentasjonsrekkefølge fra ett begrep til det andre. Det ene begrepet forutsetter altså det andre, og følgelig får vi problemer med å finne et logisk startpunkt. Vi har med andre ord enda et eksempel på at vi må velge å tro noe (Newtons lover), og først når vi bruker dem i praktiske situasjoner, vil vi oppleve om de er nyttige eller ikke.

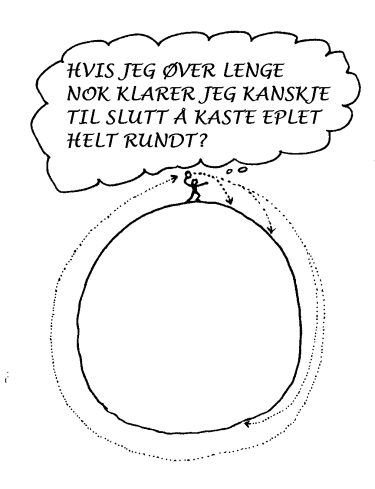
Samme lover på jorda og på himmelen
Det fortelles at Newton fikk ideen til gravitasjonsloven da han så et eple som falt. Galileo hadde da noen år tidligere kartlagt hvordan legemer beveger seg i fritt fall ved jordoverflate. Newton lurte videre på om det var de samme lovene som gjaldt for himmellegemene. Hovedforskjellen på legemer ved jordoverflata og legemer i himmelrommet er vel at alt på jorda faller ned, men månen og andre himmellegemer ikke gjør det. Om vi med bakgrunn i Newtons første lov sammenlikner månen og eplet, vil vi fort oppdage at ingen av dem har uforandret bevegelsestilstand. Eplet fikk en rettlinjet akselerasjon mot jorda da det datt. Månen går i en sirkel, men dette er også en form for akselerasjon. Et eple kan kastes og også få en bane som likner en sirkelbane. Om vi så sier at både eplet og månen er påvirket av gravitasjonskrefter fra jorda, vil det ifølge Newtons andre lov bety at de begge akselereres eller faller mot jorda. Månen faller da i en sirkelbane rundt jorda mens eplets bane før eller senere vil treffe jorda. Nøkkelen til å forstå det som skjer er å anta at gravitasjonskraften mellom jorda og ulike legemer er omvendt proporsjonal med avstanden. Det vil si at gravitasjonskraften minker jo lenger vi kommer fra jorda. Matematisk vil det si at radien befinner seg under brøkstreken i gravitasjonsformelen. Utfra den aktuelle formelen kan vi så beregne krefter på ulike legemer både på jorda og på himmelen. Når så observasjoner viser at legemene oppfører seg slik som beregningene skulle tilsi, regner vi med at formelen gir en rett beskrivelse av virkeligheten. Senere er slike formler blitt opphøyet til å kalles lover. Hovedgrunnen til dette er da at de er nyttige. Nå må det her presiseres at vitenskapen ikke kan bevise at noe er rett. Men om vi over tid ikke har klare antydninger om at en lov er feil, er det vanlig å anta at den er rett.
Newtons lover i universet
Vi skal nå se på et eksempel hvordan disse lovene kan forklare de bevegelsene som skjer i universet. Tenk deg at det bare fantes en stor og en liten masse i universet. Et eksempel er sola og jorda. Da sola har en relativt stor masse vil den ifølge Newtons andre lov, ikke få så stor akselerasjon. Vi kan for enkelthets skyld anta at sola ligger i ro. Vi vil her kort skissere fire mulige bevegelser som den lille massen (jorda) kan få etter at Gud slapp den i nærheten av den store massen:
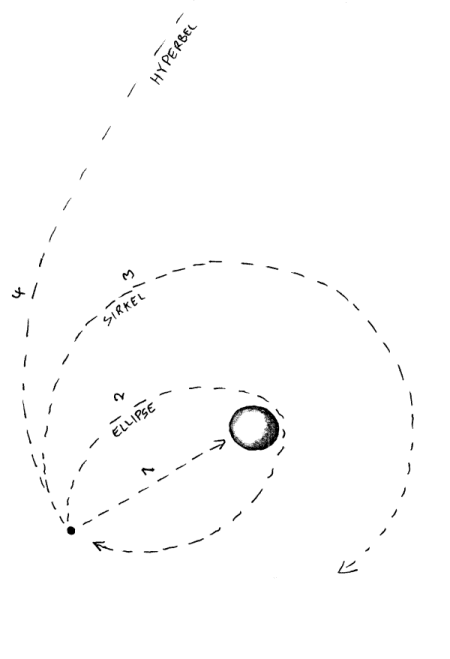
1 Hvis jorda opprinnelig lå i ro i forhold til sola ville den på grunn av kraften mellom massene falle rett mot sola. Forklar hvorfor.
2 Hvis derimot jorda hadde en liten hastighet på tvers av linja mellom sola og jorda når den ble sluppet, ville den bevege seg i en ellipsebane rundt sola. Den akselerasjonen som jorda får på grunn av gravitasjonskraften, vil delvis øke banehastigheten (så lenge jorda nærmer seg sola) og delvis forandre retningen for jordas bevegelse. Når jorda når det punktet på banen som er nærmest sola kan vi si at banehastigheta er blitt så stor at akselerasjonen "ikke rekker" å føre jorda nærmere sola. Resultatet blir at jorda vil fjerne seg inntil banehastigheta igjen blir så liten at akselerasjonen igjen "får overtaket".
3 Det er også en mulighet at jordas hastighet på tvers av retningen mellom sola og jorda var så stor at all akselerasjonen "går med" til å forandre retningen til jordas bevegelse. Banehastigheta blir i dette tilfellet konstant. Jorda vil da gå i sirkelbevegelse omkring sola.
4 Hvis jorda "slippes" med en stor hastighet på tvers av retningen mellom jorda og sola, kan det tenkes at gravitasjonen ikke vil klare å akselerere jorda så mye at "frabevegelsen blir snudd til tilbevegelse". Dette er blant annet mulig fordi gravitasjonskraften fra sola avtar med økende avstand. Jorda ville i dette tilfellet bevege seg i ei hyperbelbane som ender uendelig langt bort fra sola.
Flo og fjære
De som underviser vil av og til få spørsmål om årsaken til flo og fjære, og av og til går de da til en ekspert (vanligvis en fysiker) og ønsker en enkel forklaring som kan brukes i skolen. En lærer som underviser naturfag i grunnskolen bør da kunne forklare flo og fjære på en enklest mulig måte. Men hva er så en enkel forklaring i denne sammenhengen? Kan det f.eks. tenkes at vi voksne har lært eller pugget ting som hindrer oss i å forstå enklere forklaringer som baserer seg på et annet grunnlag enn det vi er vant til? Kan det videre være at noen forklaringer kan gjøre mer skade enn gavn, i forhold til det å forstå mer komplekse fenomen? Det finnes i utgangspunktet mange ulike måter å forklare fenomenet flo pg fjære og det er ikke noen grunn til å miste selvtilliten om man ikke forstår en dårlig forklaring. På den andre siden er det viktig at man finner fram til en forklaring som man selv forstår slik at man ikke blir svar skyldig, når elever før eller siden vil fremsette "dette vanskelige spørsmålet".
Det pedagogiske hovedproblemet i denne sammenhengen er kanskje at det finnes mennesker (også lærere) som ikke har oppdaget at tidevannet er et fenomen som er vanskelig å forstå. De har med andre ord ikke skjønt problemet, og i slike tilfeller er det vanskelig å tenke seg at de kan være til noen særlig hjelp for elever som strever med å forstå omgivelsene sine. Nå er tidevannsproblemet et sammensatt problem med mange "sider", men her i starten vil vi da nevne det som de fleste oppfatter som hovedproblemet. Nå kan det også være et problem å forstå hvorfor havvannet får en utbuling på den siden som vender mot månen, men denne er da relativt lett å forklare om vi viser til gravitasjonskraften er en tiltrekningskraft som virker mellom månen og havvannet. Dette kan da f.eks. demonstreres om vi fører en magnet over jernfilspon, stifter eller annet av jern som ligger på et bord. Vi kan da observere at haugen får en oppbuling under magneten selv om kraften fra magneten ikke er så sterk at ting letter fra bordet.
Det faglige hovedproblemet er da å forklare hvorfor havvannet vil få en utbuling også på den siden som vender bort fra månen. Her vil vi da konsentrere oss om hvorfor vi får flo på to sider av jorda og ikke fenomen som springflo, globale forskjeller på flo og fjære ol. Her følger tre forklaringen som ikke nødvendigvis er de beste:
1 Først en forklaring fra en lærebok brukt i norsk grunnskole:
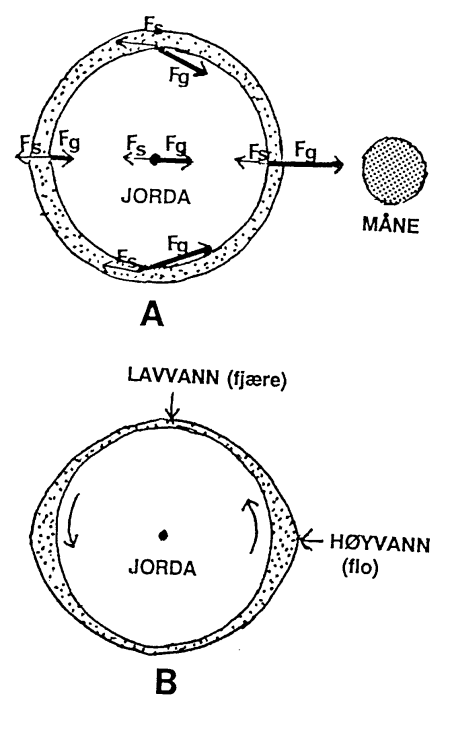
Tidevann
Årsaken til at det blir flo og fjære, forstår vi ved å se på månens og jordas bevegelser....I virkeligheten bør vi se jorda og månen som en dobbelplanet som kretser rundt et felles tyngdepunkt like innenfor jordas overflate. Det er plasseringen av dette tyngdepunktet som gjør at havet buler ut på to sider av jordkloden samtidig. Månens tiltrekningskraft trekker vannet til seg på den ene siden. På den andre siden blir vannet slynget utover på grunn av rotasjonen. (Univ.91 Nat7-9 Infobok s148)
2 Her følger så et sitat fra ei bok brukt i høyskolesammenheng. I boka Grunnleggende biologi og miljølære av Bjerketvedt og Pedersen (Landbruksforlaget 1992) kan vi blant annet lese:
c) Tidevann og tidevannsstrøm. Det er velkjent at tidevann skyldes månens og solas tiltrekningskraft på vår roterende jord. Fig. 11.9A viser en oversikt over de kreftene som oppstår på grunn av månens tiltrekning. Månens gravitasjonskraft (Fg) varierer med avstanden til månen, se fig. 11.9A. Da jorda kan betraktes som en satellitt som kretser omkring sola, vil det på jorda virke en sentrifugalkraft (Fs). Dette er en kraft som er motsatt rettet solas gravitasjonskraft fordi disse kreftene holder jorda på plass i sin bane omkring sola. Ved nymåne er sentrifugalkraften (Fs)rettet omtrent bort fra månen (se fig. 11.9A). I jordas midtpunkt er Fs og Fg like store og motsatt rettet. På den del av jorda som er nærmest månen, vil Fg>Fs og gi en resultantkraft (=tidevannskraft) inn mot månen. Steder på jorda som vender bort fra månen har en resultantkraft bort fra månen (Fs>Fg). Hvis vi tenker oss at jorda er omgitt av et sammenhengende havområde, vil tidevannskraften sørge for å trekke oseanenes vannmasser henholdsvis mot og bort fra månen. (s207)
3 I boka Havlære av Sverdrup (Fabritus 1955) kan vi lese:
Om tidevasskreftene
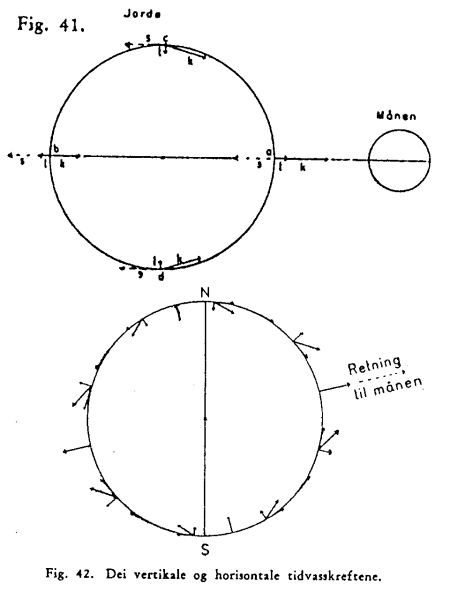
Det er ikkje lett å forstå utan viare at månen eller sola kan gje flo sjø to gonger i døgeret. Men vi skal prøve å forklare kvifior det er slik. Lat oss sjå fyrst på korleis månen og sola sviv. Vi veit at jorda sviv om sin eigen akse på 24 timar, og vi seier at månen sviv rundt jorda på omlag 28 døger. Vi seier og at månen blir halden i bana si, for di tildragskrafta mellom jorda og månen er i jamvekt med sentrifugalkrafta som verkar på månen når han sviv så og seie i ein sirkel omkring jorda. Men dette er ikkje heilt rett. Det rette er at både jorda og månen sviv om sitt sams tyngdepunkt. Dette ligg innafor overflata av jorda, for di ho har så mykje meir masse enn månen. Derfor er det berre bortimot rett å seie at månen går rundt jorda; det rette er å seie at begge sviv rundt eit sams tyngdepunkt, og at begge blir utsette for ei sentrifugalkraft som er i jamvekt med tildragskrafta mellom dei.
Samstundes med at jorda sviv om sin eigen akse på 24 timar, sviv ho omkring dette tyngdepunktet på ein slik måte at jordaksen held ved lag si orientering i verdsromet. For å skjøne rotasjonen kan lesaren teikne ein sirkel på eit papir og leggje det på bordet. Så kan han ta ei bok, halde ho med tyggen parallelt med bordkanten, og leggje papiret slik at eit bokhyrne snertar sirkelen. Deretter kan han føre boka rundt på den måten at han let bokhyrnet fylgje sirkellina, medan han held boka parallelt med bokkanten. Då gjer boka ein sirkel, og rørsla svarar til den rørsla jorda gjer rundt tyngdepunktet jord-måne på omlag 28 døger.
Det karakteristiske ved rørsla er at alle punkt på boka - og tilsvarande alle punkt på jorda - gjer nøye same sirkel. Derfor vil kvar liten masse bli utsett for nett den same sentrifugalkrafta, anten massen er på jordoverflata eller nær sentrum av jorda.
No skal vi sjå på dei kreftene som verkar på små massar på jordoverflata, men vi vil sjå bort frå tyngdekrafta som alltid verkar mot sentrum. Vi må vurdere sentrifugalkrafta og den tildragingskrafta månen har på ein slik masse (fig.41). Då må vi hugse på at tildragskrafta minkar når avstanden frå månen aukar, medan sentrifugalkrafta er den same alle stader på jorda. I sentrum av jorda er tildragskrafta og sentrifugalkrafta like store og verkar i motsette leier, men i punktet a, som er nærast månen, er tildragskrafta større enn sentrifugalkrafta, og i punktet b, som er lengst borte frå månen, er ho mindre. Ulikskapane mellom dei to kreftene vil verke som "skiplande krefter", tidevasskrefter, både i a og b, og vil vere retta utover frå jorda......
Det ville føre for langt å kome inn på dei mange og underlege drag som tidevatnet viser. Formålet med denne bolken er berre å freiste vise at vi har to floder og to fjører i døgeret, jamvel om vi har berre ein måne.
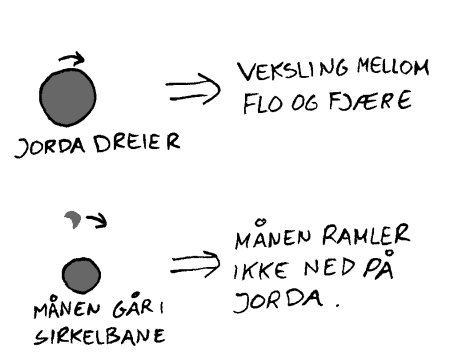
En forklaring som bygger på Newtons lover
Forklaringene ovenfor spriker litt, og det er ikke sikkert at de samlet sett bidrar til å øke forståelsen. Hensikten med å ha dem med, er å vise at det finnes ulike forklaringer på flo og fjære. Her vil jeg til slutt ta med mitt forlag til forklaring av flo og fjære. Generelt opplever jeg at mange forklaringer bringer inn mer enn de behøver. Om målet er å forklarer hvorfor "utbuling" på to sider av jorda er det ikke nødvendig å bringe inn jorda eller månens dreiing. Jordas dreiing forklarer hvorfor utbulingene forflytter seg rundt jorda og vi får flo to ganger i døgnet, men det var vel ikke hovedproblemet. Det at månen går rundt jorda (eller mer rett, om et felles tyngdepunkt) er heller ikke nødvendig for å forklare de to utbulingene. Om vi ikke hadde hatt månens dreiing om jorda, hadde vi imidlertid bare opplevd utbulingene en kort tid fordi jorda og månen ville ha kollidert. Månens sirkelbevegelse omkring jorda forklarer altså hvorfor månen ikke faller ned på jorda, men ikke tidevannsutbulingene. Generelt har vi tidligere sagt at vi kan betrakte sirkelbevegelser og lineære bevegelser som to adskilte bevegelser, og dette prinsippet vil vi da bruke her. Vi ser med andre ord bort fra sirkelbevegelsene. Vi vil så prøve å forklarer de to utbulingene direkte utfra Newtons lover som er nevnt foran.
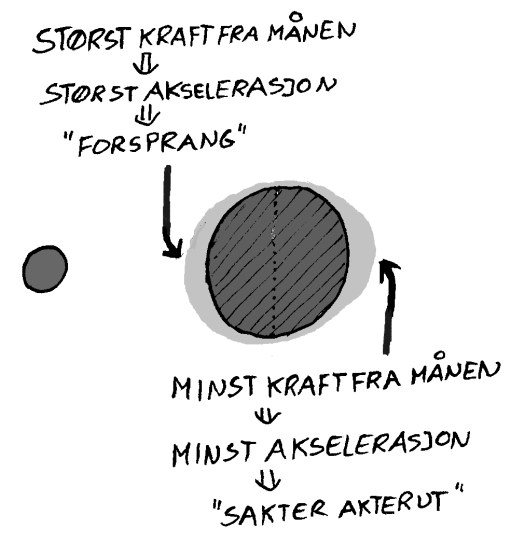

Når månen og jorda er i nærheten av hverandre, vil det virke en gravitasjonskraft mellom dem. Det betyr ifølge F=ma at de akselereres mot hverandre. Nå er det ifølge gravitasjonsloven (F=GMm/r²) slik at det som er nærmest månen vil oppleve en sterkest kraft, og følgelig vil det også akselereres sterkere mot månen. Vi får da den situasjonen at vannet som er på månens halvdel av jorda vil akselereres raskere enn resten av jorda som kan betraktes som et stivt legeme. I et stivt legeme kan vi tenke oss at gravitasjonskraften angriper i tyngdepunktet som da representere en gjennomsnittsverdi for jorda som helhet. Et stivt legeme kan ikke deformeres. Vann kan bevege seg på jorda og når vannet på månens halvdel opplever en sterkere gravitasjonskraft enn den stive jorda, vil vannet bevege seg raskere mot månen. Prinsippet er det samme som at den bilen som har størst akselerasjon vil få et forsprang i en fellesstart. Vannet har bare en viss bevegelsesfrihet. På grunn av tiltrekningskraften fra jorda vil vannet ikke kunne "forlate jord", men det vil samle seg i en utbuling på framsiden nærmest månen. Når det gjelder vannet på den andre halvdelen av jorda, så vil det oppleve en tiltrekningskraft fra månen som er mindre enn jordas tiltrekningskraft, og følgelig vil det "falle akterut". Gravitasjonskraften fra jorda vil imidlertid hindre at det forlater jorda og derfor får vi en utbuling på baksiden av jorda.
Prinsippet er kort fortalt at det som befinner seg i et vanlig gravitajonsfelt hvor feltlinjene samles i et punkt (midt i månen), vil føle en kraft som strekker legemet i retningen mot gravitasjonskilden. Det nærmeste opplever en sterkere gravitasjonskraft enn det som er fjernere.
Noen tanker om bruken av begrepet:
sentrifugalkraft
Selv om jeg opplever at den siste forklaringen er enkel
og samtidig lett "å bygge sammen med" andre forklaringer og
grunnleggende lovmessigheter i en oversiktlig tankestruktur, så regner jeg med at noen lesere kan
være uenige. Problemet er da: Hva er det som gjør at vi er uenige? Vi har jo den samme naturen rundt oss, og vanlig logikk tilsier vel at vi burde kunne enes om hva som er den enkleste beskrivelsen. Forklaringen på uenigheten i slike og liknende tilfeller er vel at vi alle har noen mer grunnleggende tanker om naturen, og vi vil vel foretrekke den forklaringsmodellen som stemmer best med det vi vet fra før. I mange av beskrivelsen er sentrufugalkraften en del av forklaringen. Tidligere har vi nevnt at dette er en såkalt uekte kraft. Den er da brakt inn for å forenkle forklaringen, fordi det synes å være en slik kraft fra vår synsvinkel på jorda. Problemet er at dette ikke er "Guds synsvinkel". Om
vi tar utgangspunkt i et referansesystem som ikke er akselerert så finnes
ikke sentrifugalkraften. Kan det være at vi gjør oss selv en bjørnetjeneste, om vi bringer inn sentrifugalkraften i slike tilfeller. Kan det være at slike begrep i neste omgang kan hindre oss i en dypere forståelse for sammenhenger? Er det slik at vanskelige forklaringer i seg selv er et tegn på at vi har valgt feil grunnlag?
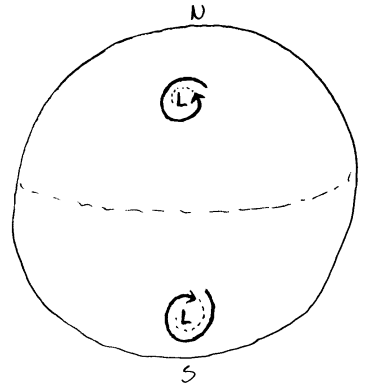
Luft som trekkes mot et lavtrykk (L) vil føle en "kraft" mot høyre på den nordlige halvkulen slik at vindren vil ha retning til høyre for lavtrykket.
Corioliskraften
Corioliskraften er en annen treghetskraft eller uekte kraft. Før har vi nevnt sentrifugalkraften. Det som kjennetegner disse kreftene er at de oppstår fordi masse har en viss treghet i et akselerert system. Nå står det vel ikke i noen fagplaner at vi skal undervise om corioliskraften i grunnskolen. Nå kan det imidlertid være noen av elevene som får høre om den og så vil vite mer om den. På den andre siden kan det vel tenkes at noen spør hvorfor lavtrykkene på værmeldingen alltid har et omliggende vindsystem som dreier mot klokka. Her vil vi kort prøve å vise at det ikke nødvendigvis er så vanskelig å forstå hvorfor alt som beveger seg på den nordlige halvkula opplever en kraft mot høyre eller "høyredreiing". Først en beskrivelse av corioliskraften fra et leksikon:
Som følge av jordrotasjonen vil ethvert legeme som beveger seg i forhold til jordoverflaten være utsatt for en treghetskraft, corioliskraften. Den horisontale komponent av denne kraft er rettet mot høyre for bevegelser på den nordlige halvkule og mot venstre på den sørlige. Dens størrelse er 2mwv sinB hvor w er jordens vinkelhastghet, v legemets relative hastighet, m dets masse og B bredden. Den vertikale komponent av corioliskraften vil, så vel på den nordlige som den sørlig halvkule, ha en tendens til å løfte et legeme som beveger seg fra vest mot øst, og til å senke et som beveger seg fra øst mot vest. Denne komponenten, som er av størrelsen 2mwv cosB, er liten i forhold til tyngdekraften. Corioliskraften må ikke forveksles med sentrifugalkraften, som alltid har en retning vinkelrett på rotasjonsaksen, og som bevirker at Jorden aviker fra kuleform. Denne kraft virker også på legemer i ro og inngår derfor i tyngdekraften. Corioliskraften er av fundamental betydning for bevegelser i atmosfæren og i havet. Dannelsen av sykloner og de store vindsystemer, passatene og monsunene, og havstrømmene er en følge av jordrotasjonen. Alle elver på den nordlige halvkule vil grave mer på høyre enn på venstre bredd, og omvendt på den sørlige (Baes lov). Mange store elver har derfor sletteland med forlatte løp til venstre, men en bratt kant på høyre bredd. I historisk tid har Indus og Eufrat flyttet seg langt til høyre, og ryinbyer ligger nå langt ute i ørkenen, mens de i gammel tid lå ved elvene. (Store Norske Leksikon)

En som går mot nord får stadig mindre dreiehastighet og vil følgelig få en svak tiltrekning mot øst som en kompensasjon for mindre dreiehastighet
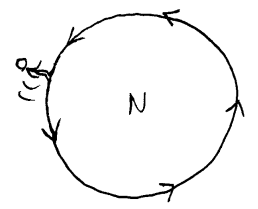
En som går mot vest på ei jord som dreier mot øst vil få mindre dreiehastighet og vil dermed oppleve mindre "sentrifugalkraft" og resultatet blir en tiltrekning mot jordaksen (nordpolen på nordlige halvkule)
Her vil vi så kort prøve å forklare corioliskraften utfra Newtons første og andre lov. Vi starter da f.eks. med å viser elevene en globus. Så forteller vi dem at vi kommer nærmere jordaksen om vi i Norge beveger oss nordover. Jo nærmere jordaksen et punkt befinner seg jo mindre er dreiefarten til dette punktet. Dette kan vi vise ved hjelp av globusen. Nå er det slik at jorda dreier mot øst, og når vi starter på en tur nordover, har vi en viss dreiehastighet. Jo lenger nordover vi kommer jo mindre dreiehastighet har den jorda vi går på og tregheten i kroppen vår vil prøve å opprettholde den opprinnelige dreiehastigheten. Derfor føler vi en "treghetskraft" østover (mot høyre). Vi kan lage et tilsvarende argument om vi går sørover. Også i dette tilfellet vil "treghetskraften" dra oss mot høyre.
Hva så om vi beveger oss vestover? Om vi ser på en breddegrad, så er den en sirkel og i en sirkelbevegelse vil "trehetskraften" trekke oss utover (mot venstre). Nå kan vi si at jorda dreier raskere enn vi går og følgelig ville vi bli dradd sørover uansett om vi gikk mot eller med jordas dreieretining. Vi kan altså ikke bruke en tilsvarende forklaring når vi beveger oss østover eller vestover. Her vil vi imidlertid bringe inn "sentrifugalkraften" i forklaringen. Denne er "balansert" av tyngdekraften og gjelder som nevnt i sitatet ovenfor både for de som beveger seg og de som er i ro i forhold til jorda. Forklaringen på høyredreiingen ovenfor var at vi fikk en endring i akselerasjonen når vi gikk nordover eller sørover. Denne endringen i akselerasjonen var da årsaken til corioliskraften. Om vi beveger oss vestover (mot jordrotasjonen) vil vi også få en endring i akselerasjon. Akselerasjonen bli mindre og følgelig opplever vi en kraft nordover i forhold til dem som er i ro på jorda. Om vi derimot beveger oss østover med jordrotasjonen får vi totalt sett en raskere dreiing enn det som er i ro på jordoverflata. I dette tilfellet vil "sentrifugalkraften" bli forsterket. Det er da denne endringen av "sentrifugalkraften" som forårsaker corioliskraften.
Denne forklaringen er kanskje ikke den enkleste, men den viser vel at det ikke er enkelt å gi en forståelig forklaring på corioliskraften. Her vil vi bare konkludere med at slike forklaringer er en god øving og test på om vi har forstått Newtons lover. Om vi klarer å forklare corioliskraften for elever i grunnskolen på en forståelig måte, så vil vel det øke både anseelsen og interessen for mekanikk hos elevene. I dag kan vi vel si at det er mange nok som velger bort fysikk.

Foucaults pendel
I 1850 ble dette forsøket første gang vist i Panthéon i Paris. Det er da snakk om en relativt stor pendel som da svinger fram og tilbake i et plan som står fast i forhold til universet og ikke i forhold til jorda. I forhold til jorda vil da planet som pendelen svinger i dreie en runde hvert døgn. Dette ble da av mange oppfattet som det endelige beviset for at det var jorda og ikke universet som dreier. På universitetet i Oslo har man hengt opp en slik pendel som man kan se via internett om man f.eks. bruker Mozilla som nettleser. Bruker man f.eks. Explorer vil man kanskje ikke se bevegelsene i sanntid.
http://www.fys.uio.no/grafikk/pendel/
Forklaringen på hvorfor denne pendelen dreier i forhold til jorda sitt referansesystem er da er da i prinsippet den samme som den som forklarer vinddreiingen rundt et lavtrykk. I begge tilfellene vil det bli en liten høyredreiing på den nordlige halvkulen som i sum gir den aktuelle dreiingen.

Massefart og dreiemoment
Mye av det som omgir oss kan forklares direkte ved Newtons lover slik som vist foran. Nå finnes det imidlertid endel fenomen som er letter å forklare og beskrive om vi innfører noen nye begrep. Kjennetegnet til disse nye begrepene er da at de uttrykker noe som er bevart i en prosess. Det er altså like mye av det aktuelle begrepet før og etter en eller annen hendelse. Energi er et eksempel på noe som er bevart i alle prosesser. Her vil vi først se på et annet begrep som likner litt på energi. Massefart er et mindre kjent begrep enn energi, og grunnen er nok at det stort sett bare brukes innenfor mekanikken. Et annet ord for massefart er moment. I disse begrepene ligger det da rett og slett et produkt mellom masse og fart: m*v. Erfaringer har vis at massefarten er bevart i når legemer støter sammen i et friksjonsfritt miljø. Om vi tenker etter er dette kanskje ikke så overraskende. Masse er et grunnbegrep som vi regner er bevart i mekanikken. Ifølge Newtons første lov vil farten forbli uendret om det ikke virker noen krefter på det som beveger seg. Derfor kan vi også regne med at massefarten er bevart mellom sammenstøt. Det nye her er da at den totale massefarten også er bevart når to eller flere partikler støter sammen. Matematisk kan vi uttrykke dette slik:
Σ mv = konstant
Vi summerer altså massefarten til alle partiklene før og etter ett eller flere støt, og vi vil da hele tiden oppleve at denne summen er konstant. Forutsetningen er at vi ikke har friksjon med tilhørende energitap i form av varme. I praksis vil vi alltid ha litt friksjon, men loven ovenfor er nyttig i de tilfellene vi kan se bort fra friksjonen siden den er relativt liten.

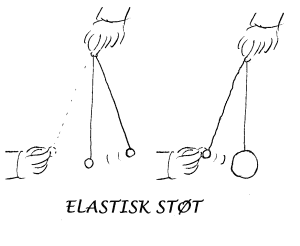
Eksempler
Om en biljardkule treffer midt på en annen som ligger i ro, vil den som bli truffet overta farten mens den først blir liggende i ro. I dette eksempelet har vi et såkalt elastisk støt og massefarten til den første kula vil overføres til den andre slik at den får omtrent samme massefart som den første. En kule som ligger i ro har massefart lik null. Om en snøball treffer en hatt vil både snøball og hatt bevege seg etter sammenstøtet. Før støtet var det bare snøballen som beveget seg. Etter støtet beveget både snøballen og hatten seg. Men siden massen til hatten + snøballen er større enn snøballens masse, vil farten til disse bli litt mindre enn snøballens fart. I dette tilfellet har vi et såkalt uelastisk støt. Massefarten er bevart i både elastiske og uelastiske støt.
Dette prinsippet kan f.eks. brukes når vi skal beregne fart til en geværkule. Om vi skyter inn i en sandsekk som henger i et tau, vil vi opplever at sandsekken får en bevegelse/fart etter sammenstøtet. Det er relativt lett og beregne sandsekkens fart etter sammenstøtet. Utfra formelen ovenfor får vi at kulas fart blir:
vk = (ms+mk)/mk * vs
Sammenstøtet mellom geværkula og sandsekken er et eksempel på et uelastisk støt. En sprettball er et eksempel på elastisk støt. Når den spretter mot bakken vil den i teorien overføre litt massefart til jorda, men siden jorda har så stor masse, vil farten til jorda i praksis bli 0 og sprettballen får da tilbake all farten. Vi får altså samme virkning som om to like baller med motsatt lik hastighet treffer hverandre.
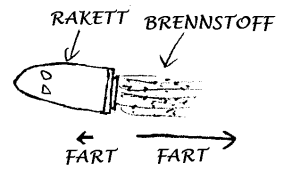
Et artig forsøk, som kanskje er litt verre å forklare, får vi om vi slipper en stor og en liten sprettball sammen. Om disse er i kontakt med hverandre når den nederste store sprettballen treffer gulvet, kan vi oppleve at den øverste lille sprettballen spretter svært høyt. En forklaring på dette er at noe av massefarten til den store overføres til den lille ballen. Vi vil ikke prøve på å forklare det som skjer her ved hjelp av massefartlikningen ovenfor.
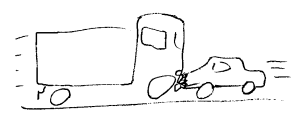
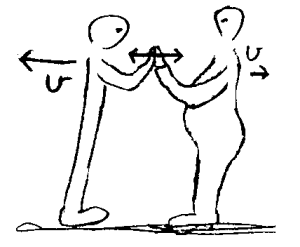
Rakettmotorer utnytter momentbevarelsen for å få fart på raketten. Forbrent gass sendes ut med stor hastighet bakover. Det vil føre til at den tyngre raketten får litt fart framover. Et eksempel på dette rakettprinsippet får vi om vi slipper en oppblåst ballong. Om en tung og lett person støter sammen vil den lette personen oppleve støtet sterkest. Dette er fordi det er han som får den største endringen i farten. Om en lastebil og en personbil kolliderer, vil det tilsvarende være de i personbilen som opplever sammenstøtet sterkest.
Vi kan velge forklaringsmåte
Det som er nevnt ovenfor kan forklares utfra at massefarten er bevart eller utfra Newtons lover. Om vi tenker på leken hvor den vinner som klarer å puffe motstanderen slik at han mister balansen når begge står med samlet føtter på armlengdes avstand, så er det en fordel å være tung. Om vi skal bruke Newton for å forklare dette kan vi si at begge vil oppleve samme kraften. Akselerasjonen blir imidlertid størst for den lette personen. Om vi i stedet ønsker å forklare dette med massefartprinsippet, kan vi si at den totale massefarten for dem begge er lik før og etter støtet. Det må nødvendigvis bety at den letteste får størst fartsendring før og etter støtet.
Talleksempler
Her følger noen eksempler hvor vi har satt inn tall i noen likninger:
Biljardkule treffer en annen (elastisk støt):
0,5kg*1m/s + 0,5kg*0m/s = 0,5kg*0m/s + 0,5kg*1m/s
Far og sønn kolliderer på skøyter.
80kg*3m/s + 40kg*(-3m/s) = 120kg*1m/s
Per kaster en snøklump (1 kg) mens han står på skøyter:
41kg*0m/s = 40kg*(-0,25m/s) + 1kg*10m/s
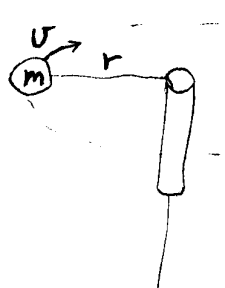
Dreiemoment
Når noe dreier har vi også en bevart størrelse som kalles dreiemoment eller dreieimpuls. Denne vil også være bevart før og etter en hendelse. Dreiemomentet er da produktet av masse, banefart og baneradius (m*v*r). Merk at det også finnes andre måter å uttrykke dette dreiemomentet. Uttrykket her viser imidlertid at dette momentet er avhengig av baneradius (r) i tillegg til v og m som er nevnt foran. Om vi vil uttrykke dette på matematisk form får vi:
mvr = konstant
Også i dette tilfellet forutsetter vi at friksjonen er så liten at vi kan se bort fra den. Om vi endrer på en av de faktorene som er nevnt her (m, v eller r) vil det medføre at en annen faktor vil endres samtidig. Dette må skje for at dreiemomentet skal være bevart. Hvis vi f.eks. øker radien til det dobbelte vil vi oppleve at farten blir halvert. Det vil skje om massen er konstant.
Eksempler
De som driver med kunstløp på skøyter benytter seg av dreiemomentbevarelsen når de endrer dreiehastighet. Om de starter dreiingen med hendene ute og så trekker disse inn vil omdreiingshastigheten øke.
I reie/disse/runse kan vi si at vi bruker dreiemomentbevarelsen for å få opp farten. Vi vil i praksis flytte tyngdepunktet inn og ut på bestemte tidspunkt. Om vi flytter tyngdepunktet mot sirkelsentrum når farten er størst vil hastigheten øke. Om vi så flytter tyngdepunktet tilbake i et endepunkt hvor farten er liten vil det få liten konsekvens for farten.
En ball henger i et tau og dreier mens snorlengden halveres. Følgende
utregning viser da at farten fordobles:
0,1kg*5m/s*1m = 0,1kg*x*0,5m
x=10m/s

