Mekanikk er et takknemlig fag når det gjelder å gjøre praktiske øvinger med enkle midler. Aktuelt måleutstyr er stoppeklokke, lengdemål (meterstokk) og kraftmåler (fjærvekt). Ved hjelp av disse instrumentene kan vi finne svar på mange typer spørsmål som det kan være nyttig å finne svar på. Først noen generelle tanker omkring elevøvinger/elevforsøk.
Åpenhet Oppgaver kan ha ulik grad av "åpenhet".
- Selve problemstillinga kan være lukket eller åpen, dvs. enten ferdig gitt eller definert slik at eleven selv må formulere problemet.
- Også metoden for å løse problemet kan være åpen eller lukket. Man kan altså si at elevene skal løse oppgaven på en bestemt måte eller la dem selv velge fremgangsmåten for å finne løsningen.
- Endelig kan løsningen karaktereiseres ved sin åpenhet. Noen problemer har en og bare en løsning som "riktig". Andre problem kan ha flere rette svar.
Ofte vil vi finne at det ikke er et enten eller, men et både og når det gjelder åpenhet. I "virkelig" vitenskap har man som regel åpenhet i alle dimensjoner. Forskeren må definere problemet og velg metode. Fasit finnes ikke og ofte vet man ikke om problemet er løsbart. Skoleoppgaver er på den andre siden vanligvis lukket. De sentralgitte planene for norsk grunnskole inneholder imidlertid målsettinger om større åpenhet i elevaktivitetene og følgende aktiviteter er da et forsøk på å imøtekomme disse målene.
Gruppearbeid
Øvingene som følger er alle forholdsvis åpne. En viktig del av øvingen går derfor med til å diskutere seg fram til en strategi og mål for øvingen. Gruppene bør derfor først sette seg sammen å planlegge før det praktiske forsøket starter. I alle forsøkene skal det gjøres målinger som skal presenteres som tabeller eller kurver. Her bør vi understreke at det bør gjøres flere målinger for at resultatet skal bli mest mulig sikkert. Man kan da lage tabeller til å fylle tall inn i. Bruk til slutt litt tid på å diskutere resultatet. Skriv gjerne ned noen konklusjoner og mulige anvendelser av resultatene. Rapporten bør inneholde figurer som viser prinsippene i forsøket, tabeller og kurver samt konklusjoner.
1 Øvingsoppgave med løsningsforslag
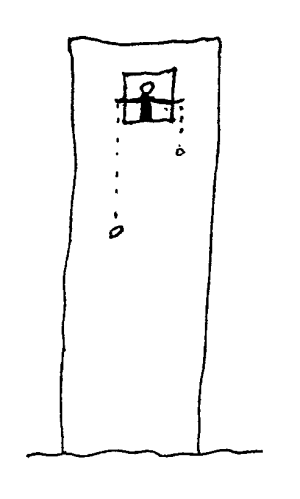
Beregn avstanden fra 2. eller 3. etasje til bakken ved å slippe ting ut av vinduet og måle tida. Lag S-T og V-T-diagram som viser hva som skjer når ting slippes ut av vinduet. Vurdere usikkerheten i beregningene.
Kommentar: Her har vi en oppgave med kanskje litt kunstige begrensninger i metode. Den mest naturlige og nøyaktige metoden ville vært å slippe ut en taustump og etterpå måle lengden av den med metermål.
Teori: Ting kan falle med tilnærmet jevn hastighet (fjær, isoporbit ol.) og med tilnærmet jevn akselerasjon (stein ol.). Bruker vi ulike metoder og velger en gjennomsnittsverdi, blir resultatet oftest best.
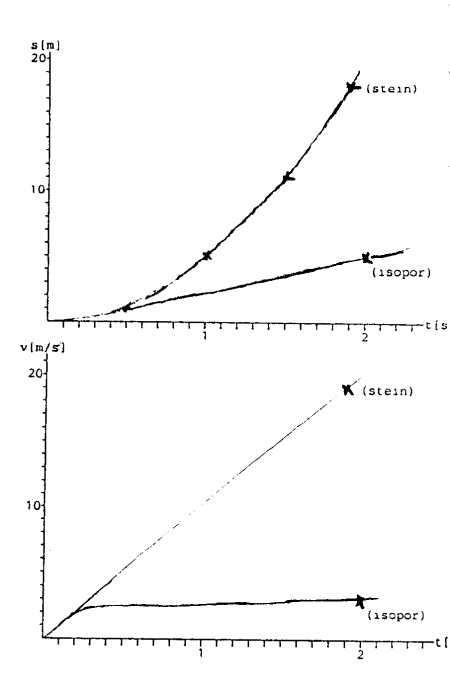
METODE 1: Antar ubetydelig luftmotstand slik at steinens akselerasjon blir 10 m/s². Slipper flere steiner og lar flere måle tiden. Antar at vi fant en gjennomsnittstid på 1,9 sek fra vi slapp steinen til den nådde bakken. Da får vi:
Vi målte tiden t= 1,9s
Vi beregnet høyden s = ½*10m/s²*(1,9s)² = 17,7m
For å tegne S-T-kurven beregnet vi flere posisjoner:
s = ½*10m/s²*(1,5s)² = 11,3m
s = ½*10m/s²*(1s)² = 5,0m
s = ½*10m/s²*(0,5s)² = 1,3m
For å tegne V-T-kurven:
v = 10m/s²*1,9s = 19 m/s (lineær når a=konst)
METODE 2: Antar at isoporbiten faller med jevn hastighet og at den oppnår topphastighet med en gang den slippes. For å finne farten til isoporbiten kan vi f.eks. slippe den fra oppunder taket og måle denne høyden (2,6 m). Anta følgende:
Vi målte tiden t = 1,0s
Vi beregnet farten: v = 2,6m/1,0s = 2,6m/s
Hvis vi så slipper isoporbiten ut av vinduet får vi f.eks:
Vi målte tiden: t = 6,7s
Vi beregnet høyden: s = 2,6m/s*6,7s = 17,4m
For å tegne S-T-kurve: s = 2,6m/s*2s = 5,2m
Kommentar: Nå samsvarer resultatene fra disse to metodene vel god. Ofte vil vi finne større sprik i dataene. Vanligvis bør både likhet og ulikhet kommenteres.
2 Fart Fang en snegle, åme, maur, eller liknende og mål hvor fort de beveger seg. Utstyr linjal og klokke. Beregn deretter hvor lang tid disse ville trenge for å gå ut til friminutt osv.
3 Strikk Utstyr: Et utvalg av strikk, kraftmåler, linjal.
Finn hvordan forlengelsen av et strikk avhenger av kraften. Mål mange sammenhørende verdier for kraft og forlengelse. Framstill resultatet grafisk. Hvis dere får en lineær sammenheng, kan dere regne ut "strikk-konstanten" k.
Gjenta forsøket for flere strikk, enkle doble ol.
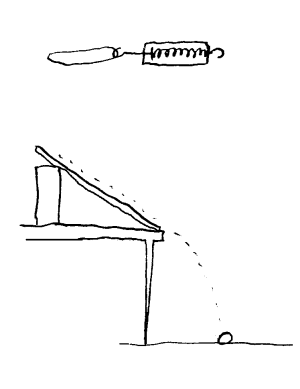
4 Hopp Utstyr: Bilbane av plast(finnes på fysikk), ulike kuler, målestav.
Om vi ordner bilbanen slik at kulene hopper ut fra bordkanten, kan vi variere ulike faktorer og undersøke når kulene hopper lengst. vi kan f.eks variere massen til kulene, høyden på overrennet, spretten på hoppkanten. Lag kurver som viser sammenhengen mellom disse. Beregn gjerne hastigheten på hoppkanten i de ulike tilfellene.
5 Beregninger av tid, fart og akselerasjon på skråplan og fritt fall
I
tilfeller hvor akselerasjon er konstant gjelder formlene:
v=s/t (def) a=(v-v0)/t (def) v2-v02=2as s=(v0+v)·t/2 s=v0t+½at2
Disse
gir sammenheng mellom de 4 verdiene: akselerasjon(a), fart(v), strekning(s)
og tid(t). Bruk disse i følgende oppgaver for å beregne de verdiene som er vanskelig
å måle:
-Slipp lekebil/klosse/kule en bestemt høyde og beregn falltid.
-Slipp
lekebil/klosse/kule på et skråplan og beregn akselerasjon og sluttfart

Utstyr: Strikk, utskytingsramp, ulike prosjektiler, kraftmåler, metermål og vinkelmål(transpotør)
Bildet til høyre viser et enkelt skyteredskap som er laget av et panelbord med spor, en bordbit, en skrue og et pakkestrikk. Et prosjektil (en trebit fra en fruktkasse) ligger klart for å bli skutt ut. Bildet viser eller ulike prosjektil av metall og tre. Pakkestrikket er festet framme ved hjelp av en fyrstikkbit slik at strikket kan strammes og slakkes etter behov og utskytingen skjer når strikket vippes opp bak.
Rekkevidden til et skyteredskap er er avhengig av ulike forhold. Hvilke? Undersøk sammenhengen mellom skytelengde og prosjektilmasse, prosjektilform og utgangsvinkel. Lag tabeller og begrunn konklusjonene ved hjelp av mekanikkforklaringer.
Finn også startfarten til noen prosjektil (ved å måle maks høyde ved tilnærmet vertikal utskyting og bruk av energisammenhengen: mgh=½mv²) og strikkraft når strikket er spent.



Utstyr: Stoppeklokke, Diverse fallgjenstander, kalkulator.
Tidtaking kan gjøres manuelt og elektronisk, men her vil vi bare bruke manuell tidtaking. Tidtaking grunnleggende for å finne fart og akselerasjon og oppgaven skal da gi øving i dette.
a) Enkel reaksjonstest
En person holder dette arket vertikalt mens en annen holder tommelfinger over tegnet sirkel klar til å gripe det når arket slippes. Tallet der fingrene griper arket angir da reaksjonstiden i sekund.
Gjør reaksjonstesten flere ganger og skriv ned egen reaksjonstid: ________
b) Manuell tidtaking
En person slipper ting fra f.eks. 1 og 2 meter og en annen person bruker stoppeklokke og måler falltiden. Hvis vi antar at akselerasjonen er konstant lik 9,8m/s² (»
10m/s²) kan vi også beregne tiden v.h.a. formelen: s=v0t+½at².
Fyll inn tall:
Høyde: _____ Målt tid:_______ Beregnet tid:______
Høyde: _____ Målt tid:_______ Beregnet tid:______
La ulike personer foreta tidtakingen og sammenlikn resultatene