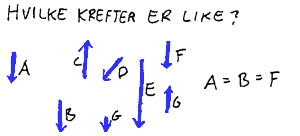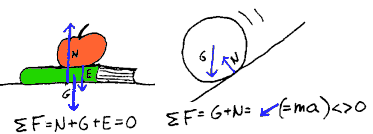Når det gjelder krefter så er det mer komplisert. En årsak er
at det finnes 3 størrelser som i dagligtale knyttes opp mot krefter
eller tyngde (tung/lett) og siden alle er aktuelle i småskolen er det vanskelig
å utsette presentasjonen av noen av størrelsene til seinere. De
3 størrelsene er:
|
|

|

|
1 kraft, tyngde, vekt
(benevning: N)
|
2 masse
(benevning: kg)
|
3 massetetthet
(benevning:
kg/dm3)
|
I småskole eller barnehage er det ikke nødvendig å gi en fullstendig oversikt
over disse tre begrepene, men vi bør heller ikke unngå å gi
en innføring i disse begrepene som har et visst slektskap i forhold til hverandre.
En viktig del av det å forstå kraftbegrepet er nettopp å forstå
at begreper brukes på ulike måter i ulike sammenhenger.
Hovedgrunnen til at kraftbegrepet er så forvirrende for både barn
og voksne er vel at vi i dagliglivet vanligvis bruker ordene vekt og
tyngde (kraftbegrep) når vi snakker om kreftene mens man vanligvis bruker kg
som benevning (massebenevning) når vi skal angi størrelser. Nå er det vanskelig å tvinge en
stor gruppe mennesker til å bruke nye ord og begrep. Her vil vi derfor
foreslå at vi tilpasser oss litt til den begrepsbruken som er vanlig,
selv om den vel er misvisende og kanskje også feil i noen sammenhenger.

For å illustrere problemet vil vi kort nevne et par sitat fra en mye brukt lærebok
i lærerskolesammenheng (Fysikkaktiviteter i barnehage og småskole
av Leif Wedøe:) som har forvirret endel lesere:
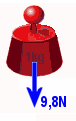
Andre (svar) er mer forståelige, men faglig gale. "Treklossen flyter
fordi den er lett." Dette bør vi ta opp separat (s 43)
Forfatteren sier her at det er faglig galt å si at en treklosse flyter fordi
den er lett. Her vil vi da kort si at det er vanlig å bruke begrepene tung lett
om massetethet (isopor er lett, bly er tungt) og påstanden til forfatteren er
derfor uheldig.
I spørsmålsformuleringen antyder forfatteren at det er galt å si at ting blir
lettere i vann. Begrepene tung og lett handler primært om krefter
(og ikke masse som forfatteren tilsynelatende mener) og forsøk
av den typen som er vist til høyre viser da tydelig at ting blir lettere når
de senkes ned i vann. Plasser pekeren på figuren og døm selv om forfatterens
påstand er rett eller feil.
Når selv voksne har problemer med de ulike kraft-størrelsene så er det ikke
rart at barn blir forvirret. Det er viktig at de voksne som lærer barna om krefter (lærerne) kjenner
den rette betydningen av de ulike begrepene, men det er ikke like viktig at
barna får hele denne forståelsen i løpet av de første
årene i grunnskolen. Det er derimot viktig at barna relativt tidlig
i skolen lærer å måle ulike krefter og dermed får et
fortrolig forhold til dette kanskje mest grunnleggende begrepet i naturfagene.

Vekt, tyngde
og kraft i dagligtale
I dagligtale bruker vi vekt og tyngde
om krefter. Når vi f.eks. snakker om vekten til bagasjen eller tyngden
til en person så tenker vi vanligvis på den kraften som disse trekkes
nedover med. Videre vil vi her si at ei vekt måler krefter (ikke masse).
Her vil vi derfor si at vekt og tyngde er krefter som er avhengig av noen ytre forhold. Disse
forholdene har da sammenheng med bevegelser og plassering i forhold til jorda.
Masse
er på den andre siden noe som bare er knyttet til indre forhold i gjenstanden. Når vi for eksempel føler oss vekselvis tyngre og lettere i ei berg-og-dalbane, kan vi slå fast at det
er vekten eller krefter som endres, mens massen
vår er uforandret. En romfarer som f.eks.
fant at badevekta viste 75 kg før han drog har fortsatt denne massen når han svever vektløs rundt i bane rundt jorda.
På månen vil han da ha en mindre vekt enn den han hadde på
jorda. Merk ellers at kraft er et mer generelt begrep enn vekt og tyngde. De
to siste brukes vanligvis om den kraften som virker nedover (tyngdekraften/gravitasjonskraften)
mens vi oftest bruker ordet kraft når vi angir krefter som virker i andre
retninger. Når f.eks. en bil bremser vil sikkerhetselene holde oss fast
i setet og i slike tilfeller bruker vi vanligvis ordet kraft.
Hva er det så som gjør at det er så vanskelig å
forstå krefter? Problemet blir vel tydeligst når vi i dagliglivet skal oppgi størrelsen
eller styrken til de aktuelle kreftene. Som nevnt ovenfor er standardbenevningen
for krefter N (Newton), men det er svært få som bruker denne
i dagliglivet. I stedet bruker vi vanligvis kg som er benevningen for
masse. Noen fysiker vil i denne situasjonen heve pekefingeren og si at det
er feil å bruke denne benevningen. Mange blir da forvirret for de skjønner ikke helt hva
som er feil. I innsjekkingsskranken sitter det kanskje en
hyggelig uniformert person som sier at vekten til bagasjen er 8 kg mens
det lenger bak i køen står en fysiker og sier at det er feil. Det
korrekte ville i denne situasjonen vært å si at massen til bagasjen
er 8 kg. Men er det lurt å prøve å innføre
et nytt ord i slike situasjoner når folk flest bruker begrep som tyngde
eller vekt? Kan vi ikke like gjerne bruke kg som benevning som vekt når
alle gjør det? Et alternativ er å si at
vekten eller tyngden er 80N. Her på jorda vil alltid en tyngdeverdi
oppgitt i N være ca 10 ganger høyere enn den tilhørende
masseverdien oppgitt
i kg. Nettopp fordi det er en slik konstant faktor (9,8m/s²) som skiller
de to verdiene vil vi her foreslå at vi i skoleverket aksepterer dagligtalen
og tillater mennesker å bruke ordene vekt, tyngde og masse sammen med
kg .Men da må vi også før eller senere si at det er snakk om
en forenkling eller tilpassing. Vi kan f.eks. si at en elev drar
i ei snor med en kraft som svarer til at han løfter 50 kg i jordas tyngdefelt.
Vi unngår altså å nevne hvor stor kraften er og i stedet sier
vi hva det svarer til i kg som er en benevning som er en
mye vanligere benevning enn N.
Masse - et ord som er lite brukt i dagliglivet
Nå er det
vanskelig nok for elevene å forstå kraftbegrepet og det er da grunnen
til at vi ikke anbefaler lærere å innføre begrepet masse
for tidlig. Om det likevel kommer opp, så bør vi
understreke at massen er en slags indre egenskap ved alle stoff. Det er noe
som er uforandret uansett hvor gjenstanden befinner seg. Masse er videre det
viktigste begrepet man bruker for å kvantifisere handelsvarer. Når
vi kjøper 2 kg hvetemel så er det egentlig snakk om en masse, men
som nevnt ovenfor gjør vi ikke noen stor feil om vi sier at tyngden
eller vekten er 2 kg.
Massetetthet
Dette er et annet begrep som ofte forveksles med masse og kraft. Vi vil komme tilbake til det i temaet
Stoff, siden massetettheten er en sentral egenskap ved ulike stoff.
Den bestemmer da f.eks. hva som flyter og synker. Her vil vi bare kort nevne at den
vanligste benevningen er kg/dm3 Massetettheten eller tettheten til et stoff er da egentlig et forholdstall mellom masse og volum. Om massen er stor i forhold til volumet så blir massetettheten stor. Hovedproblemet med dette begrepet er vel at vi i dagligtale bruker begrepene tung/lett om massetetthet i tillegg til krefter som er nevnt tidligere. Sammenhengen som disse begrepene
brukes i vil vanligvis fortelle tilhøreren hva det egentlig er snakk om.
Vi bør derfor ikke si at det er feil å bruke tung/lett om
massetetthet selv om disse begrepene primært er kraftbegrep. I grunnskolen er det derimot viktig å gjøre elevene oppmerksomme på at vi kan bruke ordet 'tung'
(fra 'tyngde') på tre ulike måter. Her følger noen eksempler:
Er
tre tyngre enn jern?
Eksempler
Når noen hevder at jern er tyngre enn tre, så mener de ikke massen men massetetthet. Når noen svarer bly når det er spørsmål om hva som er tyngst: 1 kg bly eller 1 kg fjær, så forteller det kanskje mer om begrepsbruk enn logisk tenkning. Massen (og tyngdekraften) er selvfølgelig den samme, men massetettheten er forskjellig, og det er vel nærliggende å tenke at spørreren ønsker
et svar knyttet til det som er forskjellig (ikke det som er likt). Dette er da grunnen til at mange svarer at bly er tyngst. Massetetthet er definert som masse dividert med volum eller masse pr. volumenhet
(Mt=m/V). Alt, også universet som helhet, har en massetetthet. Verdien av denne er avgjørende for hvordan ulike stoff oppfører seg. Et eksempel er om gjenstander flyter eller synker i vann. Merk at volumet til en gjenstand vanligvis innbefatter eventuelle hulrom inni. Når båter som er laget av jern flyter, selv om jern i seg selv synker, så er årsaken at hulrommene i båten bidrar til det totale volumet. Båten
består altså av både jern og luft og som helhet har den en
massetetthet mindre enn vannets massetetthet. Massetetthet har ofte benevningen kilogram pr. kubikkdesimeter. Vann får da massetettheten 1 kg/dm3. Benevningen viser ellers at massetetthet er bygd opp av to grunnbegrep. Rent filosofisk kan vi tenke oss et rom uten masse (vakuum) men ikke omvendt.

Ballen er deformert. Fører pekeren over den og se hva som skjer når den slippes fri
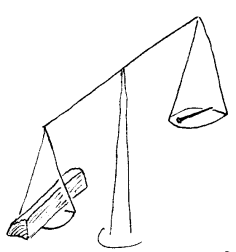
Oversikt over
begrepene elastisk og myk

Før peker
over figuren
Virkning av krefter
I tillegg til at krefter fører til bevegelser
og hindrer bevegelser, så kan vi også si at krefter former og deformerer
ulike ting. I grunnskolen kan det være nyttig å bevisstgjøre
elevene på noen begrep i denne sammenhengen. Om en gjenstand lett lar
seg deformere sier vi ofte at den er myk eller elastisk.
Forskjellen på disse begrepene er da at elastisk betyr at gjenstanden
selv vil tilbakeformes til den opprinnelige formen etter at ytre krefter har
opphørt. Jo nærmere den opprinnelige formen gjenstanden tilbakeformes,
jo mer elastisk. Eksempler er en ballong, et strikk, madrass ol. Begrepet myk
kan også brukes om slike gjenstander men det kan i tillegg brukes om f.eks.
snø eller en leirklump som er lett å forme. Leirklumpen vil da ikke tilbakeformes til
opprinnelig form men forbli deformert. Jo mykere en gjenstand er jo mindre krefter
trenges for å deformere den.
Det motsatte av myk er hard, og kjennetegnet på noe som
er hardt er vel at det kreves store krefter for å deformere det. Her er
det viktig å understreke at hard ikke er det motsatte av elastisk. Stål er
eksempler på noe som er hardt, men samtidig er det også noe av det
mest elastiske som finnes. Når stålkuler som henger i tråder
(slik som vist til høyre) treffer hverandre vil samenstøtet være elastisk og etter støtet
vil de bevege seg fra hverandre med tilnærmet samme hastighet. Forklaringen
på dette er at stålkulene deformeres litt, men det er så lite
av vi ikke ser det. Noen baller har den egenskapen at de spretter godt, og det
betyr at de er ganske elastiske, men en ball vil ikke bli så elastisk
som ei stålkule eller ei biljardkule. Noen vil kanskje protestere siden
stålkuler spretter dårligere mot gulv enn sprettballer. Poenget
her er da at det er selve gulvet som reagerer uelastisk når de treffes av
en stålkule.
Aktiviteter 1
I skolen er praktiske aktiviteter nyttig, både for å understreke
fagstoffet og for å aktivisere elevene. Aktivitetene hjelper med å "fordøye" teoristoffet eller å oppnå forståelse.
Disse aktivitetsforslagene som følger hvert kapittel er ment å være en kortfattet oversikt over enkle
aktiviteter som krever lite eller rimelig utstyr. Den enkelte lærer vil
vanligvis legge sitt preg på denne typen aktiviteter og hovedmålet
her er da bare å gi kortfattede tips, gjennom figurer og tekst. Læreren
kan da selv velge om han vil bruke tipset i forbindelse med demonstrasjoner,
bakgrunn for elevforklaringer, elevøvelser, prosjektarbeid eller annet.
Siden figurer ofte forteller mer enn mange ord, vil det i det følgende
lånt noen figurer fra ulike bøker. Disse er da nevnt i dokumentet F01bakgrunn.
I undervisningen er det viktig å ta utgangspunkt i det elevene
vet fra før, og her vil vi da anbefale læreren å la elevene
finne fram til eksempler som handler om krefter, vekt, tyngde og andre beslektede begrep.
Det er også aktuelt å la dem prøve å definere disse
begrepene. Her vil vi understreke at elevene sannsynligvis ikke vil komme
fram til så bra definisjoner som dem som finnes i lærebøker,
og det skader da ikke at de pugger noen slike definisjoner selv om de kanskje ikke
i starten skjønner alle sidene ved definisjonene.
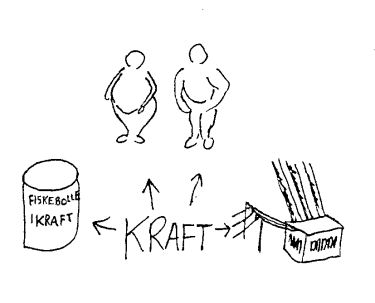
Begrepet kraft har i fysikken en mer presis betydning enn i dagligtale. I dagligtale kan vi f.eks. snakke om en kraftig person og mene at denne personen er i besittelse av krefter som gjør at han sannsynligvis vil vinne et slagsmål. Men vi kan også bruke denne betegnelsen om en person som rett og slett er feit
eller tjukk. Videre kaller vi også det som fiskebollene er lagret i for kraft. I dette tilfellet har vi en annen betydning av ordet enn den vanlige. Denne betydningen av kraft skaper vel ikke så store problemer som i de tilfellene der et ord brukes om nært beslektede fenomen. I "et kraftig smell" brukes ordet i betydningen sterkt eller stort. For barn kan slik bruk kanskje føre til at de mener at kraft har noe med lyd å gjøre. Videre brukes ordet kraft om elektrisk strøm (kraftverk, kraftpriser osv. ). Norsk
språkråd anbefaler å bruke begrepet energi i stedet (energiverk,
energipriser). Gammel vane er vond å vende, og derfor vil nok elevene fortsatt en tid assosiere kraft med elektrisitet.

Definisjon
av kraft
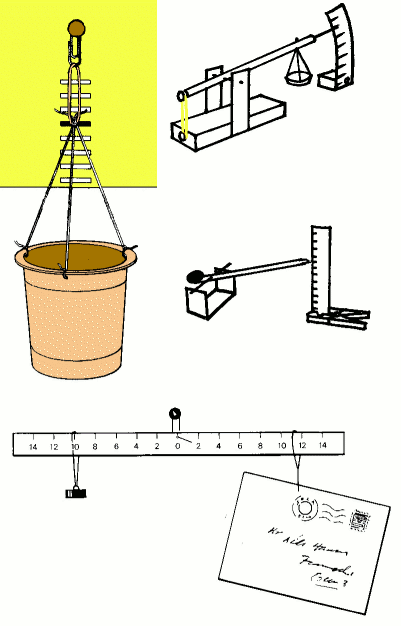
En mulig definisjon av en kraft er: Kraft er det vi måler
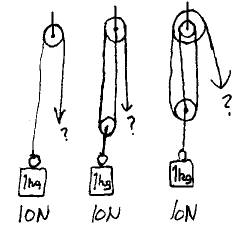
med en kraftmåler. Figuren til venstre viser da utseendet til en vanlig
kraftmåler som brukes i skoleverket og her brukes den da til å
måle kraften i snora som holder loddet oppe. Skalaen er da N (Newton).
Nå er det mulig å lage mer omfattende definisjoner av kraft som
da vil inneholde ulike begrep som masse og akselerasjon ol. Problemet
er da at disse begrepene er fjernere fra elevenes virkelighet, enn selve kraftbegrepet.
Det er da årsaken til at den enkle "sirkeldefinisjonen" ovenfor
sannsynligvis fungerer bedre i grunnskolen. Elevene kan gjøre praktiske
aktiviteter med en kraftmåler og i ettertid ha noe konkret å tenke
på når kraftbegrepet brukes.
Problemet med å knytte kraftbegrepet til en kraftmåler med Newton-skala
er at elevene kan begynne å tro at krefter er noe som bare hører
hjemme på fysikkrommet hvor man bruker kraftmålere. Det de lærer
her får med andre ord liten overføringsverdi til elevenes vanlige
virkelighet. I vår vanlige virkeligheter bruker vi da såkalte vekter
og skalaen på disse er da kg eller g. På den andre
siden kan en vekt av den typen hobbyfiskere har med på fisketur likne
ganske mye på kraftmålerene som er vist til venstre. De elevene
som tenker vil kanskje oppleve det forvirrende at man på skolen måler
N mens man ellers måler kg med samme type vekt. Om det er
et generelt mål at det elevene lærer i skolen skal være nyttig
i samfunnet ellers, så bør vi kanskje fire litt på prinsippene
slik som antydet tidligere i heftet.
Her vil vi imidlertid anbefale en alternativ til "definisjonsmetoden"
(forklaring ved å bruke definisjon) når vi skal introdusere kraftbegrepet
i grunnskolen. Denne vil vi da kalle "pekemetoden" og den går
da rett og slett ut på å "peke" på konkrete ting
når man bruker begrepet. Det er da denne metoden man bruker i barnas første
leveår, men den er brukbar langt oppover i skoleverket. En tredje metode
som vi her vil kalle "fokuseringsmetoden", går da ut
på å fokusere på eller konsentrere seg om visse egenskaper
eller kjennetegn ved kreftene når vi "peker" på dem. I
det følgende vil vi gi en kort innføring i begrepet krefter med
utgangspunkt i de to siste metodene.

Hva mener vi så med begrepet kraft i fysikken? Kraft et grunnbegrep og
der for vil vi her henvise til mange eksempler og håpet er da at leseren
ser det som er felles i disse. I de fleste eksemplene her vil vi bruke blå
farge på det som er knyttet til krefter. Målet er da at det som
leser heftet skal skjønne hva som "ligger bak" blåfargen.
Krefter er f.eks. usynlige og de er følgelig ikke blå. Men det
å reservere en farge til å representere krefter kan være nyttig
i en pedagogisk sammenheng.
Her vil vi derfor først nevne noen av de egenskapene som er knyttet til begrepet kraft.
* Krefter kan være store eller små. De har derfor en verdi eller en størrelse. I SI-systemet er benevningen for kraft N (Newton).
* En kraft har ei retning i rommet. Det som har både absoluttverdi og retning, kalles ofte vektor. En vektor kan vi anskueliggjøre ved hjelp av ei pil.
* Krefter kan enten virke ved kontakt (berøringskrefter/nærkrefter) eller på avstand (fjernkrefter).
* Krefter kan summeres. Det vil si at vi teoretisk kan erstatte flere krefter med en kraft uten at de fysiske konsekvensene
blir endret.
*Summen av alle kreftene
på et legeme som ligger i
ro vil være
lik 0.
Om å "se" krefter
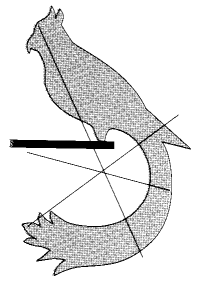
Å ikke se skogen for bare trær er et uttrykk som forteller at det kan være problemer med å gjenkjenne det vi leter etter i visse sammenhenger. Når det gjelder å påvise krefter, gjelder delvis sammen problemet. Selv om vi vet at det er krefter til stede, er de ikke alltid så lette å "gjenkjenne" dem. Gjenkjenning og tegning av krefter vil derfor være en sentral del når det gjelder å lære noe om krefter.
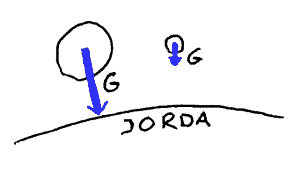
Store og små fjernkrefter
To steiner med ulik masse vil oppleve ulike krefter. Den største steinen vil oppleve størst tiltrekning fra jorda. Kraften som
trekker ting ned mot jorda kalles gravitasjonskraften (G) eller
tyngdekraften. Den virker på alle legemer som befinner seg på og
nær jorda. Denne kraften er en fjernkraft som virker selv om jorda og steinen ikke berører hverandre.
Jo større masse en stein har, jo større blir gravitasjonskraften.
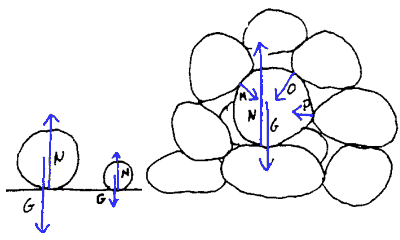
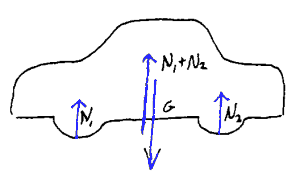
Mange krefter på samme legeme
På et legeme virker det ofte flere krefter. Da bør også tegne alle kreftene. Om steinene ligger på bakken vil det virke en kraft fra bakken på steinene. Dette er en nærkraft da den er avhengig av berøring. Slike nærkrefter blir oftest tegnet fra berøringspunktet eller det punktet der kraften virker. Kraften fra underlaget på et legeme kalles ofte normalkraften og har ofte betegnelsen N. En
stein i ei steinrøys vil da bli utsatt for mange krefter slik som figurene
til høyre viser.
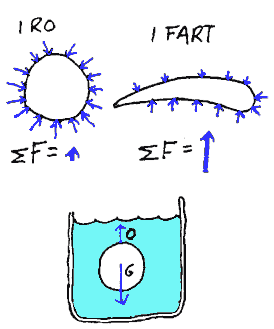
"Vanskelige" krefter
Av de kreftene som omgir oss er det noen vi til vanlig ikke trenger å ta hensyn til. Disse er ofte vanskelig å tegne og forstå. Et eksempler på slike krefter er lufttrykk. Det vanlige lufttrykket virker omtrent
likt på hele legemets overflate. Det betyr at kraftsummen er tilnærmet
lik null. Se figuren til venstre. Ved spesielle luftstrømmer vil det oppstå ulikt trykk på ulike steder. Da vil kreftene kunne summeres til en kraft som er
så stor at den kan sammenliknes med gravitasjonskraften. Denne kraften kan vi kalle oppdrift (O).På
figuren som fremstiller et snitt av en flyvinge i fart ser vi at lufttrykket er ulikt over og under flyvingen. Det kan diskuteres hvordan vi skal tegne oppdriften. For å skille denne fra vanlige normalkrefter kan vi gjerne tegne den fra oversiden av legemet
slik figuren til venstre antyder. Når vi senker et legeme ned i vann opplever vi at det blir "lettere". Også i dette tilfellet har vi en kraft som vi kan kalle oppdrift. Også denne kraften kan tegnes som en kraftpil.
Litt om summering og dekomponering av krefter
I de fleste situasjonene vil vi kunne tegne alle aktuelle krefter i et plan. I stedet for å beregne de aktuelle verdier matematisk, kan vi måle oss fram til aktuelle verdier på ei litt nøyaktig tegning. Her følger noen generelle regler og tips i forbindelse
med å tegne krefter.
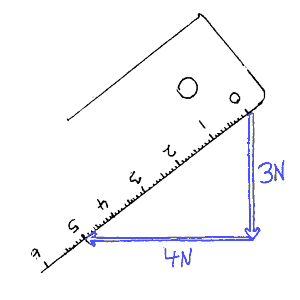
En vektor kan parallellforskyves uten at den endrer verdi. Stedet hvor vi tegner en kraft betyr ikke noe for verdien, men bare lengde og retning. Det betyr at to krefter som har samme retning(er
parallelle) og har samme verdi (lengde) er like.
(svaret på spørsmålet i figuren til venstre er at A og B
og F er like)
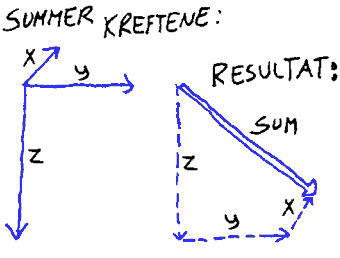
Vektorsummen fremkommer som en pil fra start til slutt i en serie med vektorer hvor hver vektor starter der den forrige endte. Det er oftest kraftsummen på et legeme som vi er mest interessert i. Summering av krefter kan skje ved å parallellforskyve kraftpilene og plassere dem etter hverandre, bakende mot spiss. Summen er da pilen som kan trekkes mellom de "frie" endene.
Kraften SUM er da summen av kreftene X, Y og Z. i figuren til høyre.
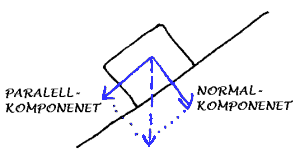
Liksom krefter kan summeres, kan en kraft også dekomponeres i to eller flere krefter for å gjøre beregninger enklere. Dette er vanlig ved skråplan. Gravitasjonskraften erstattes da av en parallell- og en normal-komponent.
Angrepspunktet for en vektor er vanligvis bakenden på pila. Når vi skal tegne krefter på aktuelle legemer, er det av
og til vanlig å plasserer bakenden av pila i det punktet som kraften angriper eller virker. Tyngdekraften virker f.eks.
på hele legemet. I dette tilfellet er det vanlig å tegne at den virker på tyngdepunktet. Om vi lager ei tegning hvor krefter faller oppå hverandre, er det vanlig å parallellforskyve en av kreftene. En stiplet linje trekkes da fra angrepspunktet til bakenden på vektoren.
Se figur til venstre.
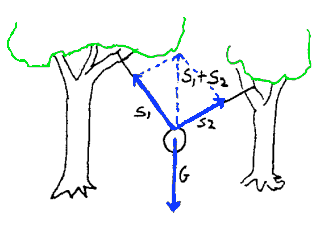
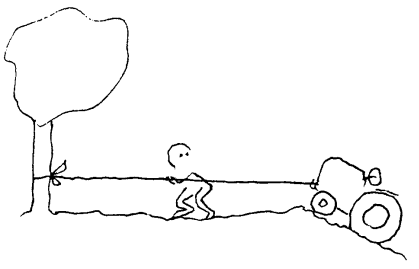
Summere og dekomponere krefter
Enkelte ganger vil en summering av krefter bety en forenkling når det gjelder å forstå de kreftene som virker på et legeme. Se eksemplet med bil og tau. Vi bruker ofte S om snordraget. Når vi summerer krefter kan vi parallellforskyve en eller flere krefter, og så til slutt erstatte de opprinnelige kreftene med en ny kraft som går mellom endepunktene.
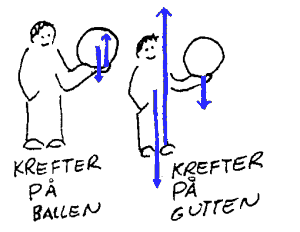
Krefter og motkrefter
Merk at vi vanligvis ønsker å finne de kreftene som virker på et legeme. Det er da viktig at vi ikke blande inn de kreftene som virker på andre legemer. I tilfellet med gutten som holder en ball, må vi derfor først bestemme oss om vi vil finne kreftene som virker på gutten eller på ballen. Merk at kraften fra handa på ballen er motkraft til kraften fra ballen på handa. Disse
to kreftene vil da være like lange, men motsatt rettet og de kalles motkrefter.
Her vil vi bare understreke at krefter alltid vil
opptrer parvis på denne måten. Det er imidlertid viktig for oss å holde de kreftene
som virker på et legeme adskilt fra de som virker på andre legemer.
Det er altså aktuelt å bare tegne de kreftene som virker på et legeme.
Om vi blander inn krefter som virker på andre legemer bli totalbildet ofte forvirrende.
Summen av kreftene på et legeme som er i ro
(eller har jevn hastighet), er alltid lik null. Når et legeme akselereres i ei retning
(får endret hastighet), vil kraftsummen være ei kraftpil med samme retning som akselerasjonen. Mer om dette i forbindelse med Newtons lover. Her
bør vi imidlertid huske at de kreftene som virker på et legeme
som ligger i ro (som ikke er akselerert) vil være lik 0. Når vi
tegner alle kreftene på et legeme som ligger i ro, så bør
kraftsummen være lik 0. I eksempelet med boka som ligger under et eple,
er kraftsummen lik 0, men det er den ikke i eksempelet hvor ballen triller nedover
et skråplan, da vi i dette tilfellet har en akselerert bevegelse.
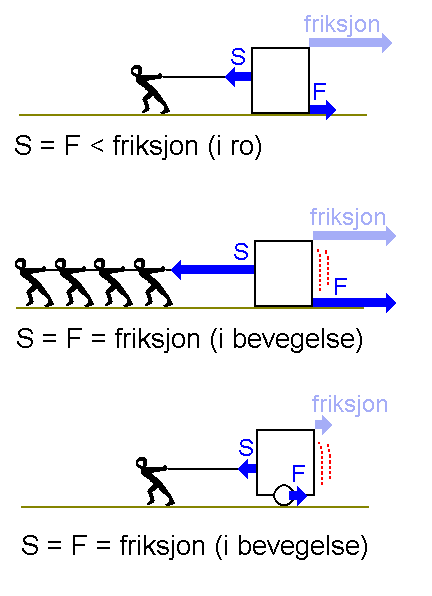
Friksjon og friksjonskraft
Ifølge L97 skal man undervise om friksjon i grunnskolen (4.kl.).
Begrepet friksjon er knyttet til nærkrefter som motvirker bevegelser.
En mulig definisjon
av friksjon er: friksjon er knyttet til maksimalkreftene som motvirker bevegelsen.
Friksjonen eller friksjonskraften virker alltid mot bevegelsen og kan
bestå av vanlig friksjon i kontaktflater, glidemotstand eller rullemotstand
i hjullager, luftmotstand og annet. Friksjonen mellom ulike stoff kan variere
mye. Mellom metall og is vil vi ha svært liten friksjon, mens gummi vil
ha forholdsvis stor friksjon i forhold til de fleste stoff. Det er da en grunn
til at vi ofte finner gummibelegget under skoene våre. Det er vel oftest
i forbindelse med bilkjøring at vi bruker begrepet friksjon. Så
lenge friksjonen mellom dekk og veibane er større enn de andre kreftene
skaper ikke friksjonen noe problem. Problemene oppstår når friksjonen
blir mindre enn de andre kreftene og det kan da forårsake at drivhjulene
spinner eller at hele bilen glir ut av veibanen. I andre situasjoner er det
ønskelig at friksjonen er minst mulig. Barnevogner, sparkstøttinger,
kjerrer, sykler, ski ol. er lettere å bevege jo mindre friksjonen
er, og i disse tilfellene oppstår problemene når friksjonen er for
stor. Generelt er det
relativt uproblematisk å kvantifisere friksjon når vi bare skal
si noe om hvor friksjonen er størst og minst. I skoleverket kan vi f.eks.
bruke et skråplan og legge ulike ting på det. Når så
helningen på skråplanet økes vil de ulike gjenstanden begynne
å gli/trille til ulike tider og vi kan da si at de som holder seg på
plassen sin lengst har størst friksjon.
Problem med kvantifisering av friksjon
Det er mer problematiske
å kvantifisere friksjonskrefter enn andre krefter. Det har sammenheng med at
friksjon og frisksjonskraft ikke nødvendigvis er det samme. Hva slags verdier for friksjon kan vi så
skrive
i arbeidsbøkene til elevene? Her vil vi ikke gå i detalj, men
bare si at det vi vanligvis kaller friksjon er et forholdstall (friksjonskoeffisient)
mellom to krefter
(Friksjonskraft/Normalkraft) og har følgelig ikke noen benevning:
Fk=F/N (friksjonskoeffisient=Frisksjonskraft/Normalkraft)
Det
er ikke mulig å måle friksjon/friksjonskoeffisienten direkte, og for elevene
(og lærerne) vil nok dette virke forvirrende. Her vil vi derfor anbefale
at man sier at friksjon er en slags kraft som er vanskelig å måle
og derfor vanskelig å finne tallverdier for. Denne muntlige koblingen
opp mot ulike krefter som de da kan måle, vil forhåpentligvis gjøre
at friksjon blir noe annet enn et nytt virkelighetsfjernt og vanskelig begrep
som de har lært på skolen.
En annen forståelse av friksjon kan være den kraften man har idé ting begynner
å gli. Men dette er da ikke en entydig verdi fordi glidefriksjonen vanligvis
vil være mindre enn den friksjonskraften man kan måle når en gjenstand ligger
i ro. Her vil vi ikke gå i dybden men bare gjenta at planene sier at vi skal lære elevene
om friksjon i grunnskolen. Siden det her er snakk om et forholdsvis kompleks
begrep er viktig at læreren vet litt om
hvilke problemer som er knyttet til dette begrepet og kanskje konsentrerer seg mest
om
friksjonskrefter i de lavere klassetrinnene. I figuren
har vi markert friskjonskraften med F og denne vil da være
like stor som snordraget (S) når det er bevegelse med jevn hastighet.
Merk at S og F har motsatt retning og når vi her sier at de er like store,
så ser vi bort fra retningen. I tillegg til de virkelige kreftene som
virker her, har vi også tegnet en lys pil som antyder hva vi vanligvis
tenker på når vi snakker om friksjon. I tilfeller hvor våre
krefter er mindre enn friksjonen, så vil vi ikke klare å bevege
gjenstandene slik den øverste figuren antyder. Figurene ovenfor viser
også hensikten med hjul, nemlig å redusere friksjonen.
Aktiviteter 2
Å gjenkjenne krefter i ulike situasjoner er viktig. I teoridelen har
vi vist til navngitte krefter i ulike situasjoner og tanken er at læreren
skal i størst mulig grad henvise til krefter når han forklarer
ulike fenomen i dagliglivet. I neste omgang er det så snakk om å
la elevene forklare ulike fenomen ved hjelp av krefter. Eksempler:
Hvilke krefter
er involvert når vi står på bakken? (tyngdekraftkraft, normalkraft..)
Hvilke
krefter er involvert
når vi løfter ting? (tyngdekraft, normalkraft, berøringskraft..)
Hvilke krefter
er involvert når vi henger i et tau? (snordrag, tyngdekraft..)
Hvilke krefter
er involvert når
vi svømmer (tyngdekraft, oppdrift..) osv.
I slike situasjoner er det
også aktuelt å tegne krefter med rett retning og rett størrelsesforhold.
Friksjon
Til høyre har vi et skråplan med ulike gjenstander på.
Ved å gjøre helningen mer eller mindre bratt kan vi så finne
ut hvor friksjonen er minst og størst og det kan da være en aktivitet
for elevene. De kan f.eks. teste ulike sko og bruke ulike stoff i skråplanet
og på den måten gjøre en slags vitenskapelig undersøkelse
av friksjonen i ulike sammenhenger.
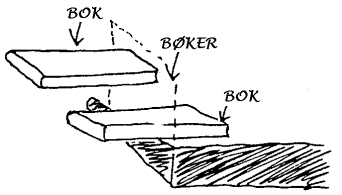
Minske
friskjonen
I noen sammenhenger er det et mål å minske friksjonen
og figurene med ei grønn bok viser et par eksempler på hvordan
man kan minske friksjonen. I denne sammenhengen kan man gi elevene noen eksempler
på noen teknikker for å minske friksjonen, og så be elevene
bruke kreativiteten og finne på nye eksempler selv. I
eksemplene nedenfor er det ellers mulig å bruke ei fjærvekt/kraftmåler
og måle hvor mye mindre friksjonskraften blir.
Når vi i mekanikken ofte behandler legemer som om de er punkter, og ikke som virkelige legemer med utstrekning, så er det for å forenkle aktuelle beregninger. Alle legemer har et punkt knyttet til seg som skiller seg ut fra alle andre punkt. Dette punktet kalles tyngdepunktet. Dette har den egenskapen at det ofte
kan "erstatte" legemet når vi studerer mekanikk. I punktmekanikken ser vi bort fra alt annet enn selve tyngdepunktet. Hvis vi tenker oss hele legemet plassert i tyngdepunktet, ville oppførselen til legemet bli lik den vi opplever i praksis. Her som eller i fysikken, er det vanskelig å lage formuleringer som er både forståelige og presise samtidig. Unntak fra forenklingen ovenfor er følgende:
1)Om legemet berører andre legemer må vi tenke at overflata er der fortsatt. Vi kan altså ikke neglisjere alt annet enn tyngdepunktet.
2)Videre forutsetter formuleringen ovenfor at vi ikke betrakter legemet fra innsiden. Graver vi f.eks. et hull mot jordas sentrum, vil den gravitasjonskraften vi føler avta og ikke øke slik vi skulle forventet om all jordas masse var plassert i sentrum. Mer om dette senere.
3) Når noe dreier om seg sjøl vil fordelingen av massen i forhold til tyngdepunktet samt dreiefarten bety noe for totalenergien. Et punkt har all masse samlet på ett sted og i dette tilfellet er det vanskelig å snakke om et punkt som dreier. I slike tilfeller forteller altså ikke tyngdepunktet alt.
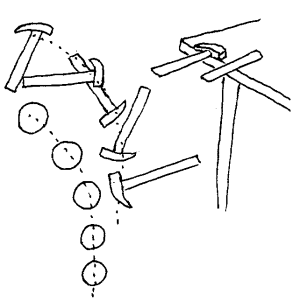
Et eksempel: Mister vi en hammer på gulvet vil den kurven den følger ofte se ganske uryddig ut. Tyngdepunktet vil derimot følge en jevn bane. Om vi konsentrerer oss om tyngdepunktet vil det være lettere å akseptere at samme lovene gjelder for en hammer som for en ball. Legger vi en hammer og en trefjøl på kanten av et bord, vil det tilsynelatende være forskjellige betingelser som avgjør når de faller. Konsentrerer vi oss om tyngdepunktene vil vi finne at samme regelen gjelder både for hammeren og trefjøla.
Hvordan finne tyngdepunktet?
Om vi ser et legeme, vil vi vanligvis tippe at tyngdepunktet ligger midt i. Det gjør det også på de mange homogene og symetriske legemene som vi omgir oss med. Eks kule, eske, bok, osv. Er derimot legemet usymmetrisk eller ikke homogent med hensyn på massefordeling, kan det være litt mer vrient å avgjøre hvor tyngdepunktet er. Vi kan henge flate legemer som pappfigurer ol. på ei nål sammen med en tråd med et lodd i enden. Tråden vil da danne ei linje over figuren. Et eller annet sted langs denne linja vil tyngdepunktet til pappfiguren ligge. Om vi så velger et annet opphengingspunkt kan vi få fram en annen linje som krysser den første. Tyngdepunktet vil da ligge i krysset mellom disse to linjene. Merk ellers at et legeme som er opphengt i tyngdepunktet vil kunne dreies i alle mulige retninger og forbli stabilt i disse retningene. Dette kan også brukes for å finne tyngdepunktet.
Dreiing om et punkt
I praksis viser det seg at mange legemer dreier når de forflytter seg. Et eksempel er en ball som ruller. I dette tilfellet vil det være energi i selve dreiingen som vi ikke kan se bort fra, om vi vil danne oss et komplett bilde av hva som skjer. Nå er det imidlertid slik at vi kan betrakte bevegelse av tyngdepunkt og dreiing av et legeme som to uavhengige element. Det betyr at vi kan gjøre beregninger på bevegelsen til tyngdepunktet og dreiingen av legemet hver for seg, og så summere disse om vi ønsker et totalbilde. Nå er det relativt komplisert å gi en komplett beskrivelse av legemer som både beveger seg og dreier. Dette er derfor ikke pensum her. Her vil vi derimot bruke litt tid på å studere dreiing i tilfeller hvor vi ser bort fra bevegelsen til tyngdepunktet.

I tillegg til forflytning, kan altså
legemer også dreie om et eller annet punkt
som vi her vil kalle dreiepunkt. Om vi ser oss rundt, vil vi kanskje oppdage at svært mye omkring oss dreier. Egentlig er det vel mer som dreier enn som forflytter seg. Hva mener vi så med dreiing. Ei dør, et hjul, en skiftenøkkel, et armledd, ei grein som beveger seg i vinden, ei skålvekt osv. har alle det til felles at de er konstruert for kunne
dreie eller forflytte seg litt. Mens vi i punktmekanikken er mest interessert i tyngdepunktet og bevegelsen til et legeme er vi i statikken også interessert i det vi kan kalle dreiepunktet eller opphengingspunktet til et legeme. Dreiepunktet til et legeme er da vanligvis det punktet hvor legemet er festet.
Forstørring
og forminskning av krefter ved hjelp av vektstangsprinsippet
De lovmessighetene som er nevnt ovenfor er nok kjent for elevene i grunnskolen. Om to elever står på hver sin side av en dør og skyver, vet de at det er en fordel å skyve hardt (stor kraft). Videre er det en fordel å skyve lengst mulig fra hengslene. Når vi likevel bør underviser dette temaet i grunnskolen så har det flere årsaker.
1) For det første er det en grunnleggende lovmessighet som gjelder i flere situasjoner. Hvis vi skal bruke en lovmessighet i en helt ny og ukjent situasjon, forutsetter det at vi har et gjennomtenkt forhold til den aktuelle lovmessigheten. Her er det altså snakk om å finne dreiepunkt og krefter i mange
ulike situasjoner. Avhengig av hva vi ønsker, kan vi ofte bruke energien vår på en mer effektiv og hensiktsmessig måte hvis vi bruker "hodet" i tillegg til "rå muskelkraft". Typisk for dette er de mange situasjonene hvor det ofte kreves relativt store krefter for å få utført ting. Det kan være alt fra hjulmuttere til store steiner i hagen. Ei vektstang kan i disse tilfellene omforme våre relativt beskjedne krefter til store krefter om vi har rett verktøy (spett, stålrør ol.).
2) Dernest vil dette vektstangprinsippet gi muligheter for flere øvinger som kan lære elevene å "tenke fysikk". Her dreier det seg om å forbedre de prosessen som går forut for en handling, samt bearbeidingen som skjer etterpå som er bestemmende for hva vi har lært. Selv om det her handler om fysiske handlinger og fenomen, så viser erfaringer at "overfysiske" tanker og refleksjoner er nyttige. Det å analysere situasjoner, trekke ut sentrale begrep og prinsipp, opparbeide et lager av nyttige ideer, og så prøve disse i tanken før de blir utprøvd i praksis, er nyttig i mange sammenhenger.
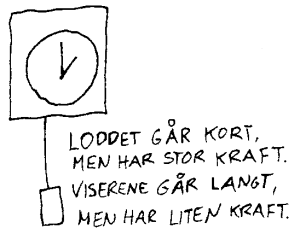
Eksempel: Bruker vi talje for å løfte ting, kan vi få omdannet relativt beskjedne krefter til ganske store krefter. Det forutsetter da at vi drar den "lette tauenden" ganske langt.
I ei klokke kan relativt korte bevegelser for tunge lodd gjøre at viserne i ei klokke kan gå ganske langt før klokka må trekkes opp igjen.
Når vi bruker tau, kjetting ol. snakker vi ofte om snordrag. Snordraget er den kraften som virker langs et tau. Et relativt lite snordrag kan bli til store krefter i et taljesystem. Tilsvarende kan et snordraget i ei stram snor bli ganske stort om vi påvirker snora med relativt beskjedne krefter på tvers. Taljer, kjeder, tannhjul er alle innretninger som kan brukes for å endre kraft og hastighet i ulike sammenhenger.
Aktiviteter 3
En
bevisstgjøring av elevene for hva vi mener med tyngdepunkt er aktuelt
i grunnskolen. I den sammenhengen er det mulig å la elevene klippe figurere
i tynn kartong og så stikke en nål gjennom figuren på ulike
steder. Tyndgdepunktet vil da alltid være rett under opphengningspunktet.
Hvis man henger et lodd i enden av en sytråd fra opphengningsapunktet
får vi ei linje som tyngdepunktet må ligge langs. Gjør man så dette
to eller flere ganger hvor vi bruker ulikt opphengningspunkt, vil vi kunne få et punkt hvor flere linjer skjærer
hverandre og dette er da tyngdepunktet. I figuren til venstre er laget slik
at den kan stå på enden av et bord.
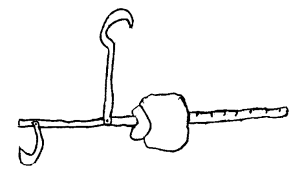
Figuren
til høyre (består av to gafler, ei potet og en tannpirker) er videre
et eksempel på en konstruksjon som balanserer på en spiss tannpirker
fordi man har ordnet det slik at tyngdepunktet havner under bordflata. Det er
mulig å lage ulike slike konstruksjoner, og det kan være en grei
øving for elevene å forklare hvorfor disse figurene balanserer.
Tilsynelatende
skulle ikke figuren til venstre balansere på den aktuelle tråden,
men fordi man har trikset litt og limt på en mynt til hver av håndflatene
vil tyngdepunktet bli lavere enn nesa.
Oppgaveeksempler:
1 Legg to blyanter litt fra hverandre på bordet og en linjal på tvers oppå. Før blyantene sakte mot hverandre, og vurder hvor blyantene ligger i forhold til tyngdepunktet på linjalen når de berører hverandre. Hvorfor vil blyantene alltid møtes ved tyngdepunktet på linjalen? Gjør forsøket om igjen når et viskelær er plassert på ene enden av linjalen. Fungerer denne metoden for å finne tyngdepunktet fortsatt?
2 Plasser ulike legemer på kanten av et bord, og formuler en regel som forteller hvilke krav som må oppfylles for at legemet skal ligge på bordkanten. Regelen må gjelde alle typer legemer?
3 Ei bok vil falle på gulvet om den legges for langt ut på kanten. Finn fram flere like bøker og vurder om det er mulig å legge disse på bordkanten på en slik måte at en av bøkene ligger i sin helhet utenfor bordkanten. Bruk ikke tape eller lim. Hvor mange bøker må vi minimum bruke. (Om det i tillegg innføres et krav om at alle bøkene skal ligge oppå hverandre er det nødvendig med minimum 5 bøker. Demonstrer dette.)
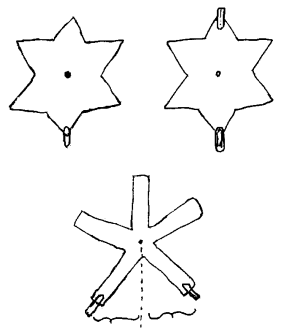
Avstanden
fra to binders til normalen gjennom opphengningspunktet vil alltid være
like
Likevektsforsøk
med pappskiver
Har vi et legeme som kan dreie om et bestemt punkt, finnes det lover eller regler for hvordan det vil oppføre seg når det påvirkes av ytre krefter. Generelt kan vi si at en kraft får større virkning jo lenger fra
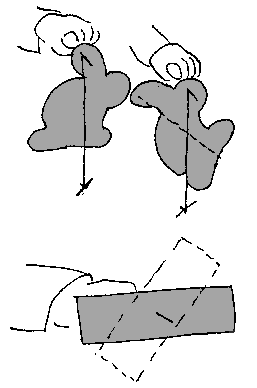
dreiepunktet/ opphengningspunktet den virker. Dessuten får den større virkning jo mer normalt den virker i forhold til linja gjennom angrepspunktet og opphengningspunktet. Dette kan illustreres om vi lager ei vektstang med f.eks. 6 armer av papp og henger denne på ei nål. Merk at opphengningspunktet skal være i tyngdepunktet. Dette kan testes ved å kontrollere at stjerna kan plasseres i alle mulige vinkler uten at den begynner å dreie.
Hvis vi så feste en binders til en av armene vil denne dreie vektstanga til en bestemt posisjon. Det er altså tyngdekraften på bindersen som er den ytre kraften som får vektstanga til å dreie. Tyngdekraften vil da dra armen med bindersen lengst mulig ned.
Plasserer vi binders på to motstående armer vil begge bindersene prøve å trekke armen ned, men fordi de prøver å dreie i motsatt retning, vil kreftene oppheve hverandre og vektstanga vil oppføre seg som om det ikke var noen lodd på den. Gravitasjonskreftene på de to bindersene er like store og avstandene til opphengningspnktet er like store.
Plasserer vi to binderser på den ene armen vil denne få overtaket og dreie ned. Størrelsen på kreftene er altså avgjørende for hvordan et legeme vil dreie. Om vi videre har en binders på hver av de motstående armene, men fester den ene litt lenger inne på armen enn den andre vil den som er lengst ute få overtaket. Det betyr at kreftene får større virkning jo lenger fra opphengningspunktet de angriper.
Nå er det ikke angrepspunktets avstand fra opphengingspunktet, men angrepspunktets avstand fra vertikallinja gjennom opphengingspunktet som er det avgjørende. Plasseres binderser på to ikke motstående armer vil vi kunne oppleve at selv om de henger like langt fra opphengningspunktet, vil den ene virke sterkere enn den andre inntil de når et punkt hvor de virker like sterkt. Når de balanserer hverandre vil avstanden fra bindersen til normalen gjennom opphengningspunktet være lik.
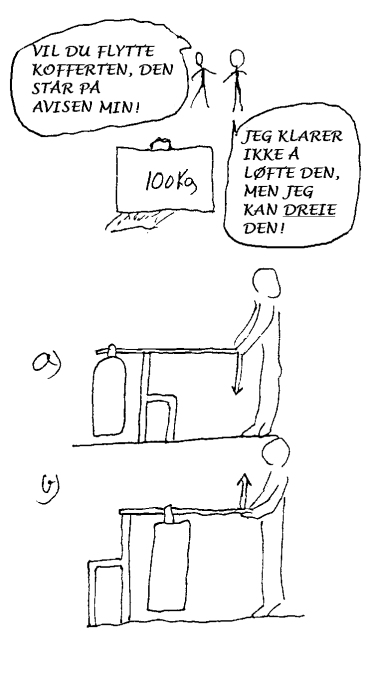
Vektstangsprinsippet for å forsterke krefter
Ved å
henvise til en jernstaur/spett, et kubein/brekkjern kan man forklare elevene
hvordan man kan bruke en slik enkel innretning for å forsterke krefter.
De kan da prøve sjøl og se hvor mye krefter de må bruke
i ulike sammenhenger.
Ei
tang, en nøtteknekker, ei dør ol. er alle eksempler på tekniske
innretninger som man bør passe fingrene sine fra for fordi det er snakk
om forsterking av krefter.
Taljesystem
for å forsterke krefter.
En annen beslektet måte å
forsterke krefter er å bruke tau og taljer. Prinsippet er da fortsatt
at kreftene der bevegelsen er lang er mye mindre enn kreftene der bevegelsen
er kort.
I eksemplet med tau og kosteskaft kan et lite barn trekke store og sterke
personer sammen uten store anstrengelser.
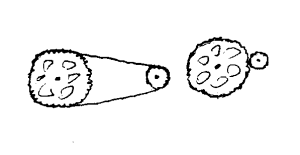
Det er også mulig å bruke tannhjul for å øke minske
krefter eller å øke minske hastigheter, men siden slike tannhjul
er verre å lage selv, har vi ikke tatt med eksempler her.
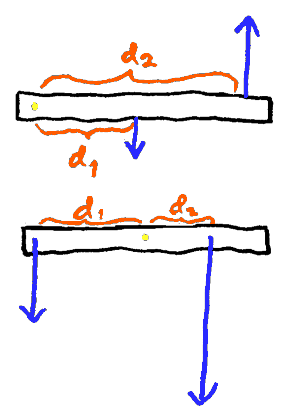
enarmet
og toarmet vektstang
4 Veiing (Måling av masse/vekt)
I det følgende vil vi kort vise en praktisk anvendelse av likevektsprinsippet som er nevnt her. Når et legeme er i ro, kan vi si at de kreftene som virker på legemet opphever hverandre. Det gjelder både de kreftene som vil forsøke å flytte på gjenstanden og de kreftene som forsøker å dreie gjenstanden. Det er "dreiekreftene" vi er interessert i her. Ved å bruke matematiske begrep kan vi formulere likevektsprinsippet slik: Betingelsen for likevekt for ei vektstang er at kraft * arm er lik i begge dreieretningene. Nå kan det være to eller flere krefter som prøver å dreie vektstanga og mer generelt kan vi derfor si følgende:
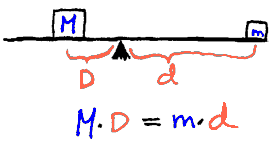
Likevektsloven:
Kraft/masse x arm vil være lik i begge dreieretningene når vektstangen
er i ro
S betyr 'summen av'. Avstanden mellom kraftens angrepspunkt og dreiepunktet kaller vi da d. Merk at F·d er et vektorprodukt. Det vil si at det vi multipliserer må stå normalt på hverandre. Om denne betingelsen ikke er oppfylt, må vi dekomponere kraften eller avstanden og så bruke normalkomponenten. Ovenfor brukte vi avstanden til normallinja gjennom opphengningspunktet, og ikke avstanden til opphengningspunktet. Dette er da et eksempel på hvordan vi kan finne et vektorprodukt uten å nevne dette ordet. Nå vet vi videre at gravitasjonskraften på alle gjenstander ved jordoverflata er proporsjonale med massen. Vi kan derfor bruke m (masse) i stedet for F (kraft) i formelen ovenfor. Har vi f.eks. ei vektstang med et lodd på hver side vil disse trekke i motsatt retning og vi kan sette opp følgende formel:
Minustegnet følger av at kreftene trekker vektstanga i motsatte retninger.
Står det N(Newton) på den vil den gi rett verdi også på Månen, men ikke om det
står kg.

Denne
fungerer både på jorda og på Månen
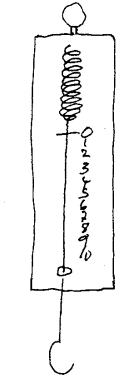
1) Fjærvekt/kraftmåler Denne typen vekt er basert på at finne visse stoff som er elastiske. Når disse utsettes for krefter vil det være en direkte sammenheng mellom lengdeendring og kraft. Videre vet vi at det er en sammenheng mellom massen til et legeme og den kraften jorda trekker på legemet. En fjærvekt består f.eks. av ei metallfjær og en skala med tilhørende viser hvor vi kan lese av hvor mye fjæra strekkes. Når vi så henger ulike legemer på fjærvekta, vil utslaget være proporsjonal med tyngdekraften. Egentlig er det en kraft som måles med fjærvekt. I skolen brukes vi derfor ofte betegnelsen kraftmåler om de fjærvektene vi bruker. Nå vet vi imidlertid at tyngdekraften er proporsjonal med massen til et legeme her ved jordoverflaten. Det betyr at vi kan skrive 'kg' i stedet for 'N' på vekta. Ei slik vekt kan da kalibreres ved å henge på lodd som vi kjenner massen til og så skrive tilhørende massetall på skalaen. Problemet med denne vekta er at elastiske materialer (strikk, stålfjær ol) vil endre seg litt over tid. Det betyr at om vi lager ei vekt av slike materialer, vil unøyaktigheten bli vel stor hvis vi skal bruke den til å måle massen til et brev. Merk ellers at en fjærvekt med kg som enhet bare er brukbar på jordoverflata. En fjærvekt med N som enhet er også brukbar på nånen. Hvorfor?
2) Skålvekt Grunnprinsippet i den andre typen vekt er at det er to verdier som sammenliknes. I utgangspunktet trenger denne et tyngdefelt for å virke, men de vil fungerer like godt på månen som på jorda. En betegnelse på denne vekttypen er skålvekt. Dette er en type vekt som kan gi bestemme massen relativt nøyaktig forutsatt at vi har lodd som har nøyaktige verdier. I de fleste skoler finnes skålvekter sammen med et sett med lodd. Sammen med loddsettet følger vanligvis en pinsett. Grunnen til at denne medfølger er at massen av loddene vil kunne endres om de får fingeravtrykk på seg. Derfor er regelen den at loddene bare skal behandles med pinsett. En vanlig skålvekt har to like skåler og avstanden til dreiepunktet er fast for disse. Ifølge vektstangprinsippet som er behandlet ovenfor, er da regelen at denne er i balanse når massen i de to skålene er den samme. Denne typen vekt er litt tungvint og bruke. Grunnen er at vi for hver veiing må plukke ut lodd som nøyaktig balanserer det vi ønsker å veie, og så må vi til slutt summere loddene. Videre ville det være for omfattende å la elevene lage alle de loddene som trenges om vi skulle bruke en slik komplett vekt. Merk at prinsippet bak denne vekta er at vi varierer massen og lar vektarmene være fast.
3 Vekt med ett lodd
Ifølge vektstangprinsippet vil både masse (m) og avstand (d) være med å avgjøre når vekta balansere. I en vanlig skålvekt må vi variere massen i den ene skåla for å finne massen til det vi skal veie. Hvis vi i stedet lar massen være fast og så varierer avstanden (d) til opphengningspunktet kan vi også finne et balansepunkt. Denne typen vekt finner vi ofte på kjøkken og hos kjøtt eller fiskehandleren. De som bruker den slipper å holde orden på masse lodd, og veiingen går derfor relativt raskt. Et lodd kan flyttes fram og tilbake i ulike hakk
i tillegg til at det oftest kan finjuseres ved hjelp av dreiing. Avstanden mellom hvert hakk kan da svare til f.eks. en kg. Dreiing av loddet kan så gi en mer nøyaktig verdi for hvor mange gram fisken er over eller under en hel kg.
4 Vekt med vinkelskala
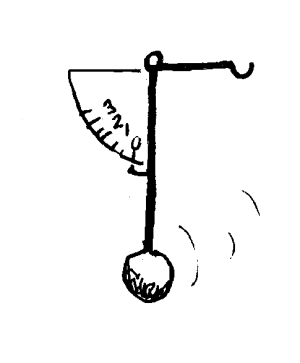
Ovenfor har vi vist hvordan vi kan variere masse og vektarm for å balansere vekta. Ved å telle opp lodd eller lese av en skala kan vi så beregne massen til det vi skal veie. Kanskje litt overraskende finnes det enda en måte å bruke vektstangprinsippet til å måle masse uten å endre på hverken masse eller vektarm. Nøkkelen her er at vi lar vekta selv variere armen. Ved å la en relativt stabil stiv pendel dreie ut av likevekt som følge av at vi legger noe på vekta, vil vi kunne lese av en vinkel som da kan gi oss en verdi for massen til det som legges på vekta. Den vekttypen som er skissert her er nok den raskeste å bruke siden vi slipper justering etter at brevet er lagt på vekta. Merk at denne vekta vil få relativt lite aksjonsområde.
Aktiviteter 4
Bruke ulike vekter
I utgangspunktet mener vi at barn tidligst mulig bør lære å
kvantifisere krefter.
Den som ønsker å lære barn å bruke penger (handle)
på egen hånd vil sannsynligvis inkludere tallverdier i undervisningen,
og mye tyder på at vi også må inkludere noen tallverdier i
et undervisningsopplegg om krefter. Her følger da noen aktiviteter hvor
barna selv kan være med å finne noen verdier for krefter med kg
og g som benevning. I teoridelen har vi begrunnet dette og for ikke
å bli arrestert for å undervise vranglære kan vi si at de
aktuelle kreftene "svarer til å løftet xx
kg".
Kreftene som omgir oss varierer svært mye i størrelse. Det er
da grunnen for at vi ikke kan bruke bare en benevning. Listen nedenfor viser
4 vanlige benevninger:
Det som skiller disse er da en faktor på 1000. I skolen kan det være
aktuelt for elevene å måle de tre nederste og under følger
noen eksempler på vekter som kan brukes:
Badevekta gir kg som benevning
Kjøkkenvekta
gir kg og g som benevning
Skålvekta gir g
og mg som benevning og gir relativt nøyaktige verdier
Brevvekta
gir g som benevning
Elevøvelser er vanligvis en lukket aktivitet på den måten at både framgangsmåte og resultat er gitt på forhånd. Slike aktiviteter kan styrke og utvikle gode rutiner, som er nødvendige i mange sammenhenger, men de appellerer relativt lite til kreativiteten. Mange i dagens skole etterspør en mer åpen aktivitet hvor kreativitet og selvstendighet spiller en større rolle. Prosjekt har vært et moteord
i den senere tid, og mange har lurt på om det er mulig å engasjere elever i praktiske og nyttige aktiviteter hvor det er snakk om å anvende forståelse til å gjøre noe nyttig som da ikke bare er en gjentakelse av hva andre har gjort før oss. I
det følgende vil vi skisser noen aktiviteter med en relativt åpen
innfalsvinkel
Oppgavetype 1: Vei ulike ting med ulike tilgjengelige vekter.
Oppgavetype 2: Lag en hjemmelaget vekt
Manghe har bruk for ei brevvekt og her vil vi kort gi noen tips i denne sammenhengen.
Både hjemme og på skolen finnes det ofte en stolpe eller en vegg som vi kan feste ei nål til. Derfor foreslår vi her å bruke en eller annen form for stiv papp og ei knappenål som opphengingspunkt. Videre vil vanligvis et brev kunne henge i en binders, og derfor vil vi her anbefale å bruke en binders i stedet for ei skål. Her anbefaler vi å lage den siste typen vekt (vekt
med vinkelskala) og denne har behov for et lodd. Bly er et tungt metall
(stor massetetthet) som er lett å forme, og blyplater brukes blant annet for taktetting. Ved hjelp av ei vanlig saks kan vi da klippe oss små biter som vi fester ved å brette dem rundt pappen.
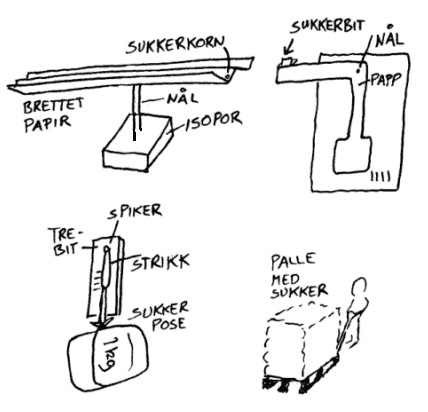
Påvisning
av små og store krefter
Figurene til venstre viser noen tips i forbindelse med veiing av store og
små masser. Hvis vi skal måle
krefter må vi lage en kraftmåler som er tilpasset se vektene man ønsker å måle:
-vektstenger som
balanserer på en spiss eller henger i et tau er vanligvis mest følsomme
-pendler
som presses ut av likevekt er også følsom for små krefter
-strikk-
eller fjærbaserte innretninger trenger større krefter for
å gi utslag
-forflytning av større gjenstander krefter
vanligvis store krefter og er derfor mindre aktuelle i grunnskolen.
Lag selv noen vekter og sammenlikn tyngden til ulike gjenstander. Eksempler:
insekt, nål, mynt, papirark osv. Anslå vekten i kg, g eller
mg. når du får oppgitt at en 10øre veier 1,5g.
Et eksempel på et konkret undervisningsopplegg:
Lage ei brevvekt
Ei vekt som skal måle masse kan baseres på ulike prinsipp:
1
strekke ellastisk fjær og observere forflytning på skala (kraftmåler, badevekt)
2 balansere
ved å endre masse (skålvekt),
3 balansere ved å forflytte
masse (kjøkkenvekt)
4 observere utsving til et lodd på en skala|(brevvekt).
Utstyr: klosse med hull, spiker/stift, trelistbit med hull, pappbit, hyssing, blybiter, binders, strikk, stein oa.
Eske med lodd kan brukes til kalibrering.
Oppgaven er å selv lage en vekt som kan bestemme om et brev skal frankeres over/under 20g eller 50g
basert på ett av prinsippene som er nevnt ovenfor. Vekten i seg selv skal bare bestå av billige materialer av typen som er skissert ovenfor, men det er da lov å bruke ei eske med lodd under kalibreringen. Det skal videre oppgies øvre og nedre grense for masser den kan måle (rekkevidde) samt usikkerhet (± 1g eller liknende formulering).
De ferdige vektene kan så bedømmes av en jury som består av klassen og i denne sammenhengen vektlegges funksjonalitet, estetikk og pris.
Figuren til venstre viser noen tips.
Bruke
vippe som vekt
I barnehager og skolegårder finnes ofte ei vippe av den typen
hvor det sitter et barn på hver side og vipper opp og ned. Slike kan da
brukes til å veie ting med, og her følger noen ideer hvordan vi
sammen med elevene kan veie hverandre ved hjelp av ei vippe.
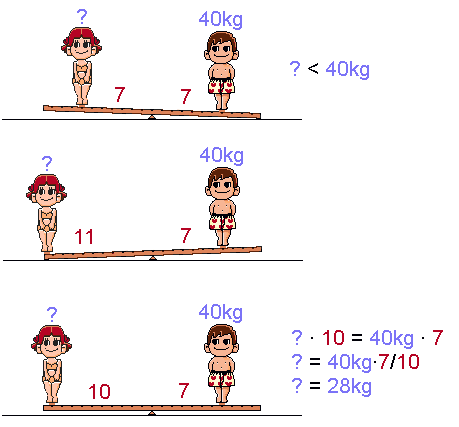
Prinsippet kan også vises ved hjelp av en bjelke og ei trekantlist slik
som vist på figuren til høyre. Forutsetningen for å bruke
en slik planke som vekt er at man kjenner en vekt (40kg i tilfellet til høyre). For at målingen
skal bli mest mulig nøyaktig har vi også lagt ut to relativt smale
lister som elevene skal balansere på. Disse gjør det da enklere
å måle avstandene fra dreiepunktet til de to personene. Merk at
vekten må balanseres før forsøkene begynner.
Den enkleste måten er å plassere barna like langt fra dreiepunket
og da ser vi at gutten er tyngre enn jenta (øverste figur). Om vi derimot
skal finne en konkret verdi for jentas vekt, så må vi først
balansere vekten ved å f.eks. flytte på jenta og deretter måle
avstanden fra opphengningspunktet til de to barna. Formelen til høyre
viser da hvordan man kommer fram til verdien. Det er ikke meningen at elevene
i de laveste skoleklassene skal utføre denne utregningen, men det kan
være nyttig for dem å være med å måle avstander
og kan f.eks. læreren gjøre selve utregningen.
Her følger videre noen andre ideer til hvordan man selv kan lage ulike vekter.
Når det gjelder kalibreringen (det å finner tallverdier som kan
plasseres på en skala) så anbefales det å bruke lodd med kjent masse, men det
er da også mulig å bruke et hulmål som f.eks. litermål. Vi vet da at 1 l vann veier 1 kg og derfor
kan vi kalibrere vekta med vann.
Litt om måling og usikkerhet
Å måle er i prinsippet å sammenlikne to størrelser. Den størrelsen som brukes som referanse kalles enhet. Forholdet mellom størrelsen og enheten er da et tall, kalt måltallet. Enhver måling vil altså innebære en viss usikkerhet og noen praktiske tips er nevnt nedenfor.
Nøyaktighet
Anta at vi måler ei stang seks ganger og får resultatene:
0,753m 0,758m 0,756m 0,753m 0,755m 0,754m
Gjennomsnittsverdien av tallene blir på en kalkulator: 0,754833m.
Hvor nøyaktig bør vi så oppgi dette tallet? Det største avviket fra denne verdien er:
0,758m-0,754833m = 0,003167m
Utfra aktuelle målinger kan vi ikke utelukke noen verdier innenfor området mellom største og minste målte verdi. Om vi betrakter gjennomsnittstallet ovenfor, kan vi kan være rimelig sikker på at siffrene 0,75 er rett. Tallene fra og med 3. siffer kan derimot være feil. Vi kan da si at usikkerheten ligger i det 3. siffer. Å ta med flere siffer er meningsløst. Etter vanlig standard er det vanlig å ta med det første usikre siffer. Vi sier at usikkerheten ligger i det siste siffer. Skal vi følge denne standarden bør lengden på staven oppgis til å være 0,755m. Om vi vil angi en usikkerhet kan det skje på følgende måte: l=(0,755±0,003)m.
I eksemplet ovenfor har vi 3 gjeldene siffer. Usikkerheten ligger da i det siste. Merk at nuller til venstre i tallet ikke regnes med når vi teller antall gjeldene siffer. Når det gjelder 0-er til høyre i et tall, så regnes disse med til antall gjeldene siffer når tallet er skrevet på 10-potensformen.
Et eksempel. Lyshastigheten er funnet til å være 299793 km/s. Om vi skriver dette tallet på 10-potensformen blir det 2,99793 108 m/s med 6 gjeldende siffer. Om vi heller ønsker å skrive ovennevnte tall med 3 gjeldene siffer blir resultatet: 3,00 108 m/s.
Om slike tall inngår i en formel/regnestykke med +, -, * og / har vi en tommelfinger-regel som sier at svaret ikke bør ha flere gjeldene siffer enn den oppgitte størrelsen med færrest gjeldene siffer.


Om vi bretter et ark til trekant, firkant, femkant og sirkel kan vi undersøke
hvilke konstruksjon som er vanskeligst å velte.
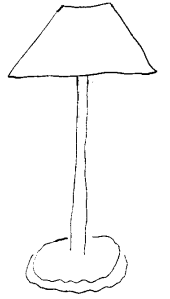
Om
man gjør lampefoten tung vil tyngdepunktet trekkes nedover.
Vi omgir oss til daglig med mange ulike konstruksjoner som i tillegg til andre oppgaver også bør være stabile og solide. Et kjennetegn på mye av det barn lager, enten det er hytte eller annet, er at de ofte mangler disse to egenskapene. Ingeniører studerer i mange år for å lære seg å lage solide og stabile konstruksjoner. Det er ikke meningen at vi skal lære alt dette til elevene i grunnskolen. Noen prinsipp kan imidlertid være aktuelle. Det hender ofte a elevene skal lage ulike enkle konstruksjoner. Om de klarer å gjøre disse stabile og solide er avhengig om de forstår visse grunnleggende fysiske lovmessigheter.
Mobilitet krever stabilitet
Når vi lager noe som ikke kan festes til underlaget fordi det skal være mulig å flytte på det, er stabilitet et vanlig krav. Et eksempel er ei vanlig stålampe. Er den ikke stabilt kan den velte og bli ødelagt. En hovedregel er at en gjenstand balanserer om vertikallinja gjennom tyngdepunktet faller innenfor støtteflata. Dette er imidlertid ikke nok om vi ønsker ei stabil lampe. Her vil vi kort nevne to prinsipp som gjelder når vi skal vurdere hvor stabil en gjenstand er:
1) Støtteflaten bør tilfredsstille visse betingelser. Om gjenstanden velter vil den i praksis dreie om ei linje, og denne linja kan vi da betrakte som ei støttelinje. Jo lenger det er mellom de ulike støttelinjene, jo mer stabil vil konstruksjonen være. Generelt kan vi si at det er avstanden fra loddlinja gjennom tyngdepunktet til støttelinjene som er en viktig faktor som bestemmer hvor stabil en lampe er. Tilfeldige krefter som prøver å dreie gjenstanden ut av balanse, vil da ha mindre sjanse til å lykkes om avstanden fra loddlinjen til støttelinjene er lang. Noen eksempler. Jo nærmere bilens hjul er plassert til de fire hjørnene, jo mer stabil blir den. Jo mer kvadratisk en firkantet støtteflate er, jo mindre sjanse er det for at gjenstanden skal velte. Størst avstand blir det imidlertid mellom støttelinjene hvis støtteflata er rund.
Derfor brukes ofte rund sokkel på stålamper ol. Kontorstoler har ofte 5 føtter i stedet for 4. Dette gir større stabilitet og dessuten vil en slik stol fortsatt kunne stå om en fot knekker.
2) Tyngdepunktet bør være lavest mulig. Hvis ikke dette er tilfelle, vil vi kunne oppleve at relativt små krefter eller bevegelser vil kunne få gjenstanden ut av balanse. Eksempler: På biler er motor og tunge deler plassert lavest mulig. Stålamper og annet som må være høge har ofte et lodd nederst for å trekke tyngdepunktet nedover. Da blir de mer stabile.
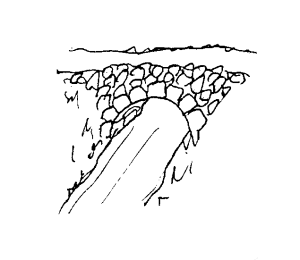
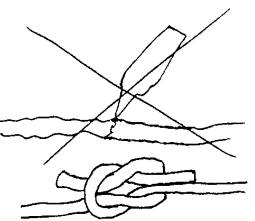
Tau blir vanligvis
knyttet og ikke limt fordi lim aldri blir så solid som "originalen".
Svak "lim" kan kompenseres av solid konstruksjon
De materialene vi bruker og de festemetodene som finnes (spiker, lim osv) har begrensninger når det gjelder styrke. Når vi skal konstruere noe som skal være solid, følger vi ofte visse prinsipp for hvordan ting skal settes sammen eller konstrueres. I gamle steinkirker og steinbroer har man vanligvis ikke brukt noe bindemiddel for å holde ting på plass. Når disse er så solide som de er, skyldes det selve konstruksjonen. Steinene som er brukt er solid på et område. Det er f.eks. relativt enkelt å slå i stykker eller knekke en stein om vi anvender kreftene rett. Derimot er det vanskelig å klemme sammen stein slik vi kan gjøre med f.eks. en svamp. Hvis vi så i steinkonstruksjoner ordner det slik at storparten av kreftene som oppstår går med til å klemme sammen stein vil vi kunne oppnå svært solide konstruksjoner. Her følger andre eksempler som viser at konstruksjonsmetoden betyr mye for hvor solid en gjenstand er:
Når vi knytter to tauender i stedet for å lime dem, er årsaken at limflata sjeldent blir like solid som tauet. Friksjonen i knuten kan derimot bli sterkere enn tauet. En god knute vil strammer seg til når den belastes. Derfor er det ofte ikke selve knuten som er det svake punktet.
Bruker vi spiker i ulike bærekonstruksjoner, bør vi unngå at kreftene på spikerfestene blir slik at spikrene trekkes ut. Belastningen på et gulv kommer oftest ovenfra og derfor bør vi spikre gulvet oppå bærebjelkene.
Bærende konstruksjoner i biler, hus, menneskekroppen og andre byggverk har visse former som ofte går igjen. Generelt vil vi unngå at visse punkt blir belastet med spesielt store krefter. Prinsippet er å fordele krefter på størst mulig område. Eksempler:
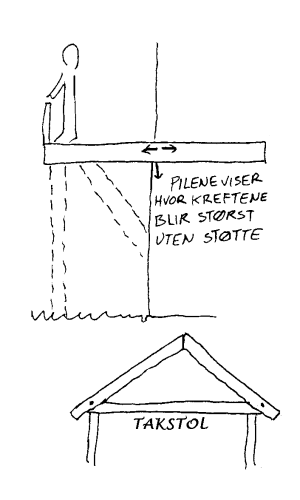
En veranda vil ofte stikke et stykke ut fra huset i horisontal retning. Beveger vi oss så på denne vil belastningen på verandaen bli større jo lenger fra veggen vi befinner oss. Når verandaen ikke har noen støtter ytterst vil de kreftene som holder verandaen oppe bli svært store der den er festet til veggen. Kraften her kan bli mye større enn kraften fra personen til verandaen. Årsaken er vektstangsprinsippet som er nevnt tidligere. Derfor er det viktig at veggen er solid under bærebjelken. Videre er det også viktig at selve bærebjelken er solid så den ikke knekker. En måte å avlaste de store kreftene som oppstår ved lange horisontale utspring er å lage skråstøtter. Disse vil ta opp mye av de kreftene som ellers vil bli svært sterke i et bestemt punkt. Finn ulike eksempler hvor skråstøtter brukes for å gjøre ting mer solid.
Et annet eksempel: Et tak på en garasje kan være flatt. Om spennet til de bærende bjelkene blir langt, vil presset på bjelken bli urimelig stort. Den kraften snøen på taket presser ned med midt på stokken, må nemlig overføres til veggen via bærebjelken. Det oppstår i denne sammenhengen et relativt stort strekk på undersiden av bjelken. Dette kan bli så stort at bjelken knekker. Om vi plasserer en støtte midt på bjelken vil strekket på undersiden av bjelken reduseres betraktelig. En alternativ takkonstruksjon er da et vanlig skråtak som bæres av såkalte takstoler. Uten å gå i detalj om denne typen takkonstruksjoner, er prinsippet at kreftene fra snøen på taket, overføres til veggene via krefter i lengderetningen på bjelkene i stedet for krefter på tvers av bjelkene.
Aktiviteter 5
På den ene siden kan det være nyttig for elevene å
lære å observere hva som gjør at ulike gjenstander (møbler
ol) er mer eller mindre stabile. En samtale med utgangspunkt i ting man har
tatt med til timen er nyttig i denne sammenhengen. En annen type aktivitet er
å be elevene lage mest mulig stabile eller solide konstruksjoner ved hjelp
av f.eks. papirark, klosser ol.