


30.10.03 Erling Skaar
Bygger på Emne 9
Målet for aktivitetene i dette heftet er å forstå de elektriske grunnprinsippene som gjelder i en strømkrets og kunne anvende dem i praktiske situasjoner. Begrepene strøm(I), spenning(U), effekt(W) og resistans(R) og sammenhengen mellom disse (U= RI og P= UI) er grunnleggende i all elektronikk. Andre sentrale begrep som blir behandlet er leder, isolator, kortslutning, sikring, seriekobling og parallellkobling. I praksis er dette en repetisjon av deler av emne 3
Om undervisningsopplegget:
Elektronikkpuslespillet er en samling av elektriske
og elektroniske komponenter som kan kobles sammen til forskjellig utstyr.
Den som vil lære noe om elektrisitet trenger teori eller informasjon.
De første sidene er med for å gi en teoretisk bakgrunn for
resten av opplegget. Men det er først når vi prøver å
anvende teorien i praktiske situasjoner at vi virkelig lærer. Heftet
inneholder også endel oppgaver og tanken bak er at de skal
være en kontroll på egen forståelse. Den som klarer oppgavene
har sannsynligvis forstått fagstoffet. Her bruker vi ordet prosjekt
om noen av de praktiske oppgavene hvor det er snakk om å lage nyttig
utstyr og anvende det i ulike sammenhenger. Prosjektbeskrivelsen er relativt
kortfattet og det er da opp til de som gjør prosjektet og finne
nye anvendelser og gjøre forbedringer. Mange har ellers fortalt
at de først forstod fagstoffet etter at de hadde arbeidet med å
formidle det videre til andre, og derfor vil vi her oppfordre leseren til
å lage nye oppgaver og prosjekt i tillegg til de som er nevnt her.
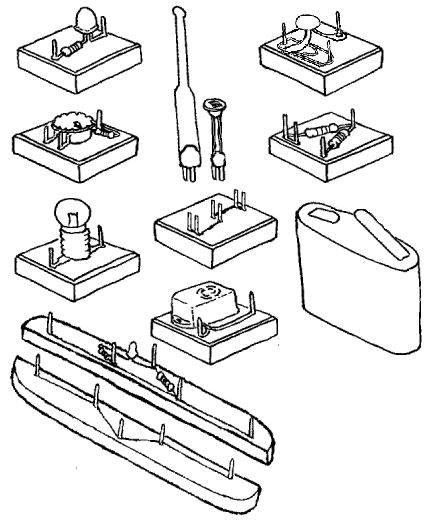
Utstyrsoversikt (m/ nyttige data)
En kvantitativ definisjon av strøm
I lærebøker er det vanlig å definere strøm
som ladningmengde pr. tidsenhet. Dette er da en kvantitativ definisjon
som er nyttig når vi skal finne hvor mye strøm det er snakk
om i bestemte situasjoner. Den samme definisjonen kan også uttrykkes
med symboler og vi får da: I= Q/t . De tilhørende standardbenevningene
er A= C/s (ampere = coulomb/sekund). Nå er det relativt vanskelig
å måle ladningsmengden Q og derfor er denne definisjonen mindre
nyttig i praktiske situasjoner.
En kvalitativ definisjon av strøm
Når vi skal arbeide med strøm trenger vi en forståelse
vi strøm som hjelper oss til å forstå ulike praktiske
situasjoner: Vi trenger med andre ord en kvalitativ forståelse av
hva strøm er, og her følger da en slik kvalitativ definisjon:
| Strøm er elektroner som forflytter seg i samme retning |
Dette er da en definisjon som det kan være nyttig å huske. Her følger så litt om bakgrunnen for denne utformingen og valg av begreper. Noen definisjoner bruker begrepet ladninger i stedet for elektroner for at definisjonen skal bli mer generell. Når vi her bare nevner de negative ladningene (elektronene), så er det fordi det er disse som vanligvis forflytter seg når det går strøm. Å velge det mer generelle begrepet ladning innebærer en generalisering som sannsynligvis skape en unødig avstand mellom teori og praksis. Det er videre verd å merke seg at elektroner alltid vil bevege seg litt fram og tilbake (termiske svingninger eller vibrasjoner). Det som kjennetegner disse bevegelsene er at de har tilfeldig retning og summen av slike bevegelser i et område vil da være tilnærmet null. Når vi har elektrisk strøm er det derimot snakk om at flere elektroner beveger seg i en retning enn i de andre retningene, og vi kaller da dette en forflytning. Merk ellers at definisjonen bruker "elektroner" i ubestemt form, og i praksis er det snakk om et mindretall av elektronene som forflytter seg, mens det store flertallet ikke forflytter seg. Merk videre de elektronene som forflytter seg fra batteriets minuspol til lederen ikke er de samme som de som forflytter seg fra lederen og over til batteriets plusspol. Strøm består altså av mange elektroner som flytter seg en liten bit hver. Når vi snakker om strøm, tenker vi da at elektronene beveger seg i et salgs stafettløp og ikke i et vanlig lengdeløp hvor samme deltaker passerer både startstreken og målstreken.
Merk eller at vekselstrøm skifter retning med jevne mellomrom. Dette er da fortsatt strøm ifølge definisjonen ovenfor. Her vil vi da i hovedsak konsentrere oss om likestrøm. Det vil si at strømmen hele tiden har en retning.

Strømretningsproblemet
Da menneskene oppdaget fenomenet som vi kaller elektrisk strøm,
så var man uheldig og definerte elektronladningen til å være
negativ. Man visste den gang ikke hvilke vei de bevegelige partiklene (elektronene)
beveget seg og dette valget gjorde da at elektronene fikk negativt fortegn.
Siden pluss og minus er motsatte størrelser betyr det at forflytningen
av negative elektron vil bli motsatt av den positive størrelsen
som vi kaller "elektrisk strøm". Vi sier altså at strømmen
går fra batteriets plusspol gjennom strømkretsen til minuspolen,
mens elektronene som i praksis forårsaker denne strømmen da
vil gå andre veien. Dette er en konstant kilde til forvirring i elektrisitetsopplæringen
og en mulig medvirkende grunn til at mange har gitt opp. Problemet kunne
vært løst om man internasjonalt hadde blitt enig om å omdefinere
elektronladningen fra minus til pluss, men da måtte også alle
lærebøker skrives om. Så langt har man latt være
å gjøre noe, og resultatet er sannsynligvis at alt som har
med elektrisitet å gjøre fremstår som vanskeligere enn
det egentlig er. I disse heftene har vi valgt å konsentrere oss om
"strømretningen" som da er den positive størrelsen siden
dette er vanlig i de fleste bøkene. Men det betyr da at hver gang
vi skal prøve å forstå virkemåten til enkeltkomponenter
så må vi "koble om" og tenke "elektronstrømretning"
som da er den motsatte retningen.
Kvantitative definisjoner av spenning
Nå finnes det mange måter å definere spenning. En
mulig kvantitativ definisjon: Spenning er forholdet mellom effektoverføring
og strøm. Om vi bruker symboler kan det samme uttrykkes ved
følgende formel: U= P/I . Effekten (P) er videre definert
som energimengde pr. tid (P= E/t) og siden strøm er definert som
ladningsmengde pr. tid så vil en enkel matematisk utledning hvor
vi forkorter bort tiden gi følgende alternative kvantitative definisjon:
Spenning
er energi pr ladning med formel: U= E/Q. Siden det er lettest
å måle strøm og effekt er den første formelen
mest aktuell når vi skal finne spenningsverdier. Den andre definisjonen
er derimot mest nyttig når vi skal forstå hva spenning egentlig
er. Standardbenevningen for spenning er volt og sammenhengene mellom benevningene
blir da: U= W/A= J/C (volt = watt/ampere = jule/coulomb)
En kvalitativ definisjon av spenning
Elektrisk spenning er mer diffus enn elektrisk strøm og derfor
er det vanskeligere å forstå spenningens rolle i praktiske
situasjoner. Her følger et forslag på en kvalitativt definisjon
av spenning som er nyttig når det gjelder å forstå spenningens
rolle i konkrete strømkretser:
| Spenning er det (en kraft) som driver/skyver/drar elektronene |
Kraft er et begrep innenfor mekanikken som kan forårsake forflytning av mekaniske gjenstander. Spenning er da det tilsvarende begrepet innenfor elektromagnetismen som kan forårsake forflytning av elektron. Spenning er da en slags kraft som oppstår mellom polene i en strømkilde (eks batteri) og den vil da fordeles på alle elektronene i strømkretsen. Merk at vi her bruker begrepet "elektronene" i bestemt form for å antyde at alle elektronene i kretsen vil oppleve en kraft som skyver/drar dem litt ut av likevektsposisjonene.
En forutsetning for all elektrisitet er at man kobler visse komponenter sammen i det vi kaller en strømkrets. En strømkrets er da en krets (lenke, kjede) av komponenter som leder elektrisk strøm. En viktig forutsetning for at det skal gå strøm er at kretsen er sluttet (sirkelformet, ikke brudd). En av komponentene i en strømkrets må videre være en strømkilde (batteri, generator/dynamo eller batterieliminator/transformator + likeretter). Det er da strømkilden som driver strømmen som da har ulik virkning i de ulike komponentene. En mulig definisjon av en strømkrets:
| En strømkrets er en krets/ring med ledende materiale som inkluderer en strømkilde |
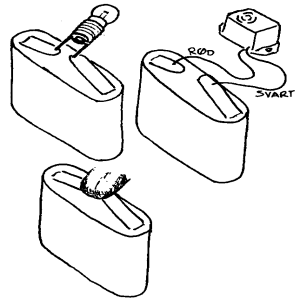
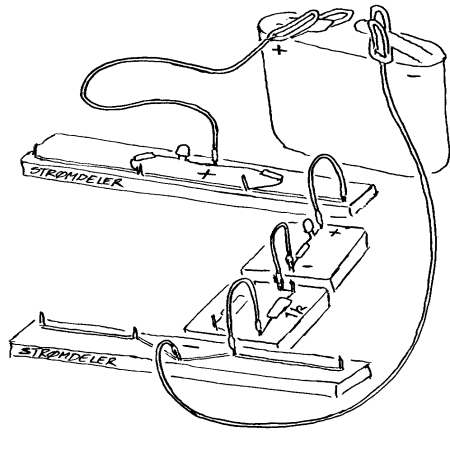
Hvordan lære om det "usynlige"? Et kjennetegn på begrepene strøm, spenning, resistans og effekt er at de er "usynlige". Det vil si at vi ikke kan oppdage dem direkte ved hjelp av de vanlige sansene. Den pedagogiske eller didaktiske utfordring er da å unngå at man knytter disse begrepene opp mot fysiske gjenstander, figurer eller andre distraherende faktorer og dermed henger seg fast i vrangforestillinger som da vil hindre en rett forståelse. Figuren viser at det er mulig å se, høre og kjenne strøm fordi strømmen kan lage henholdsvis lys, lyd og nerveinpulser i tungen, men slike erfaringer er egentlig ikke til så stor hjelp når det gjelder å forstå strøm. Det er altså ikke slik at erfaring med strøm nødvendigvis gir kunnskap om strøm. I skoler og annen opplæring er det vanlig å bruke tekst og figurer/bilder, og her vil vi da understreke at dette er uunværlige hjelpemidler også i såkalt praktisk undervisning. Generelt er det vel slik at tekster kan uttrykke det meste, men det er ikke nødvendigvis slik at det er lett å tilegne seg det som står i ei tekst. En figur eller et bilde kan på sin side "fortelle mer enn mange ord", og mange vil si at figurer/bilder er uunværlige i de fleste undervisningssammenhengene. Men figurer/bilder kan også være mer eller mindre nyttige i forhold til å forstå ulikt fagstoff, og her vil vi derfor kort kommentere tre ulike typer grafiske figurer som vi bruker i dette opplegget.

1 Avbildning
I dette elektronikkopplegget vil vi arbeide med ulike strømkretser
og en avbildning er da en tegning eller et bilde som viser komponentene
i strømkretsen slik de ser ut i virkeligheten. Det er viktig å
se den fysiske situasjonen hvor man bruker de ulike begrepene i og slike
avbildninger er da med på å knytte fagstoffet opp mot den fysiske
virkeligheten. Slike avbildninger bidrar altså til å trekke
beskrivelsene "ned på jorda" slik at man unngår at undervisningen
blir teoretisk og virkelighetsfjern. Avbildninger er også effektive
i forbindelse med praktiske instruksjoner. Med bilde eller figurer kan
man relativt lett vise hvordan man skal utføre bestemte handlinger.
Hovedproblemet med avbildninger er kanskje at de har med uvesentlige ting,
som kan henlede oppmerksomheten i feil retning. De er videre vanskelige
å forenkle på en rasjonell måte slik at huskearbeidet
blir lettere. Generelt kan vi si at kunnskap består av "huskestoff"
og "forståelse" og det er da et faktum at "husketiden" avtar når
kompleksiteten øker. I dette elekronikkopplegget vil vi bruke endel
avbildninger i starten, når strømkretsene er relativt enkle,
men metoden blir ubrukelig når kretsene blir litt større.
2 Koblingsskjema
For at man skal kunne fremstille mer kompliserte elektriske kretser
er det utviklet en standard måte som kalles koblingsskjema. Hensikten
er å beskrive hvordan de ulike komponentene er satt sammen på
en mest mulig enkel og oversiktlig måte. Man bruker da skjema som
består av symboler og streker. De enkelte komponentene har da fått
tildelt ulike symbol som da er enkle grafiske figurer og lederne som kobler
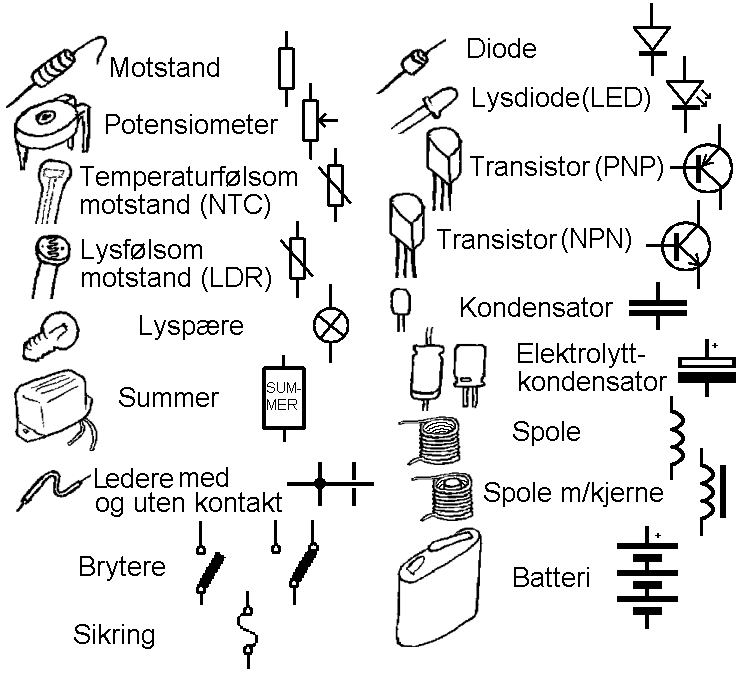
komponentene sammen er da symbolisert med enkle streker. Irammen ovenfor vises tegninger av noen vanlige komponenter sammen med navn og
symbol. Figuren lenger oppe visere en mellomting mellom symboler og tegning av
brikkene som vi kommer til å bruke litt her fordi det er lettere
å bruke puslespillet om figurene i veiledningen likner på det
ferdige produktet.

3 Tankemodeller
Som nevnt tidligere er det viktigste som kjennetegner en strømkrets
usynlig og den enkleste formen for hjelp til å forstå det som
ligger bak er vel å tilføye litt tekst til figurer.
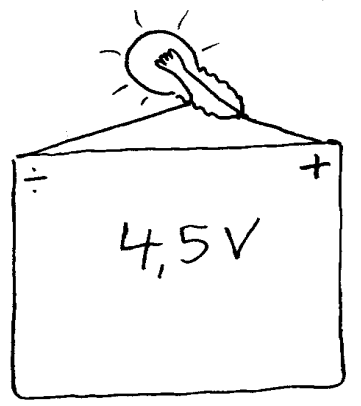
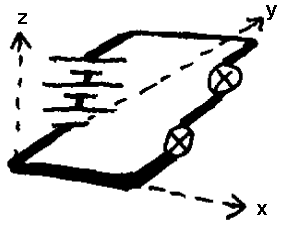
En annen fremstillingsmåte er å bruke flere dimensjoner for å få fram visse sentrale sider ved de ulike kretsene. Begrepet elektrisk spenning er f.eks. et diffust begrep for mange og om man lager en tredimensjonal figur hvor ulike høyder betyr ulike spenninger, så kan dette være en hjelp til å forstå spenningens rolle i en strømkrets. På figurer vil da strømmen "renne nedoverbakke" mens batteriet "pumper den opp igjen". Slike tankemodeller hører da med i en innføringsperiode. En som kan elektronikk vil da "se" spenningen og andre grunnleggende prinsipp når han ser et koblingsskjema, mens nybegynnere ofte trenger litt "starthjelp".
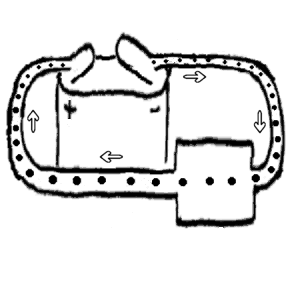
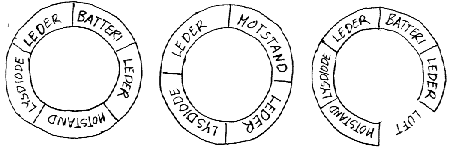
Det er også mulig å lage tredimensjonelle figurer som da kan fortelle noe om hvorfor det går strøm eller ikke i bestemte kretse. Til høyre vises noen eksempler hvor batteri, lyspære, lysdiode og motstand er tegnet tredimensjonelt hvor z-aksen representerer spenningen. Tallene på batteriet angir spenningen og jo høyere høydeforskjell man får jo større blir spenningen som drar/skyver elektronene rundt i strømkretsen. Merk at kreftene fra batteriet virker på elektronene langs hele strømkretsen, og grunnen er da at elektronene drar/skyver på hverandre innbyrdes. Denne tankemodellen er da nyttig for å forstå grunnleggende prinsipp. Den aktuelle koblingen har bare en "vei" som strømmen kan gå, og det betyr da at det går like mye strøm hele veien rundt. Strømmen vil derfor være lik i alle deler av en strømkrets. Dette kalles Kirschoffs 1. lov. Når det gjelder spenningen på ca. 4V, så vil den fordele seg med ca. 2V på hver av lyspærene.
En lysdiode tåler ikke å bli utsatt for en spenning på 4V og motstanden beskytter da lysdioden når den "bærer" ca. halve spenningen. Det at batteriets spenning fordeles på de ulike komponentene kalles Kirschoffs 2. lov. Alt som befinner seg på samme høyde har da samme spenning og her er det verd å merke seg at en leder vil ha samme spenning i hele sin lengde. En måte å forklare dette er at elektronene forflytter seg så lett i en leder at de vil være raske til å utjevne eventuelle spenningsforskjeller. Merk ellers at elektronene trekkes oppover utenfor batteriet (tenk luftbobler) mens strømmen trekkes nedover (tenk gravitasjonskraft).

Hovedbegrepene i dette heftet er strøm
og spenning. Siden vi ikke kan se disse direkte, er det nyttig å
bruke modeller eller bilder som da er noe som har visse likhetstrekk med
strøm og spenning, men som ikke er strøm og spenning. Om
du ikke er vant til å bruke modeller kan det virke forvirrende å
se eller lese mange ulike fremstillinger av hva som menes med strøm
og spenning. Her vil vi bare si at du fortest mulig må prøve
å få tak i hva som er det sentrale i modellene/bildene. Å
forstå modeller/bilder er da i praksis å kunne skille bort
alt uviktig og så sitte igjen med det sentrale som man da kobler
sammen med begrepene strøm og spenning. Mange ulikemodeller kan
derfor hjelpe oss til å unngå å fokusere på feil
ting når vi skal prøve å forstå hva strøm
og spenning egentlig er.
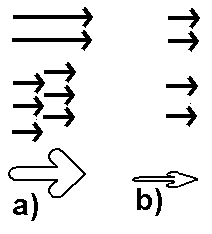
Det er vanlig å tegne strøm
som piler. Merk at strøm ikke er piler, men pilene henleder oppmerksomheten
vår til sentrale egenskaper ved strøm. Retningen på
pilen viser hvilke veg elektronene eller en tenkt positiv strøm går
(motsatte retninger). Lengden på pilene kan da si noe om størrelsen
på strømmen. Det samme gjør antall piler. Det vanligste
er å markere store og små strømmer med tykke og tynne
piler.
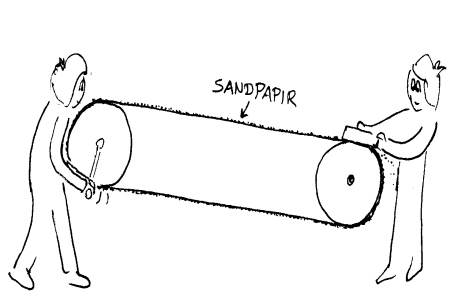
I noen sammenhenger er man interessert i å
få fram energisiden ved en strømkrets og i slike sammenhenger
kan man f.eks. bruke sandkornene i et sandpapir som bilde på det
som skjer i en strømkrets.
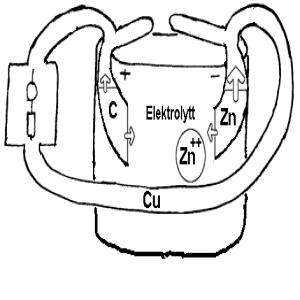
Når det gjelder spørsmålet om hva det er i batteriet som lager spenningen, så vil vi ikke gå noe særlig inn på dette her. Generelt bør vi først lære hvordan spenningen virker utenfor batteriet før vi lærer hvordan den oppstår inni batteriet. Men for at ikke noen skal oppleve batteriet som en forvirrende svart boks, vil vi her kort nevne at spenning vanligvis vil oppstå når to ulike elektroder er stukket ned i en såkalt elektrolytt. Figuren til høyre viser at disse metallene kan være karbon og sink. Ulike stoff vil ha ulik antall elektronhull og det vil i neste omgang bety at de kan oppstå ulikheter i hvor mange elektroner som trekkes i de ulike retningene i en strømkrets. Hvis denne kraftsummen blir forskjellig fra null vil vi totalt sett få en strøm av elektroner i den ene rertningen.
En enkel strømkrets
Til høyre vises en grunnleggende strømkrets
med koblingskjema. Hensikten med lysdioden er da å vise om det går
strøm. Lysdioden vil lyser når det går strøm,
og motstanden på 330Ω
vil da beskytte lysdioden mot å få for mye strøm/spenning.
Lag en kretsen som er vist her. Mulige grunner til at lysdioden ikke lyser:
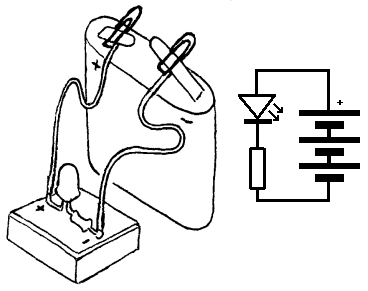
Kretsen ovenfor bruker relativt lite strøm (ca. 8mA). Den kan derfor være oppkoblet en stund uten at batteriet tappes noe særlig.
Ledere og isolatorer
Hva leder strøm? En viktig egenskap ved stoffene som omgir oss
er om de leder strøm eller ikke. Hvis et stoff leder strøm
kaller vi det en leder. Om det ikke leder strøm kaller vi
det en isolator. Hvis vi kobler andre ting inn i kretsen som er
vist over, kan vi se på lysdioden om disse gjenstandene eller stoffene
leder strøm. En lysdiode kjennetegnes ved at den trenger relativt
lite strøm for å lyse, og derfor vil denne kretsen kunne påvise
relativ små strømmer. Mer om dette senere.
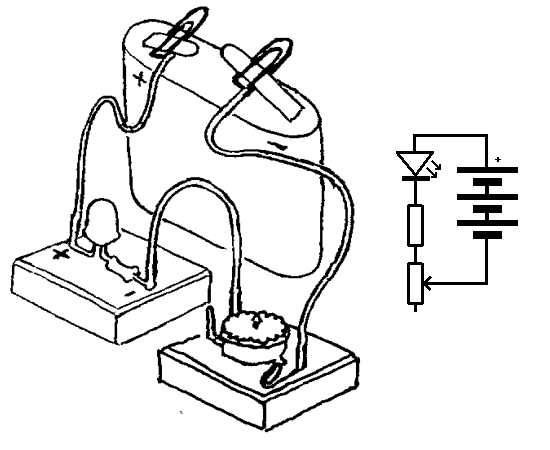
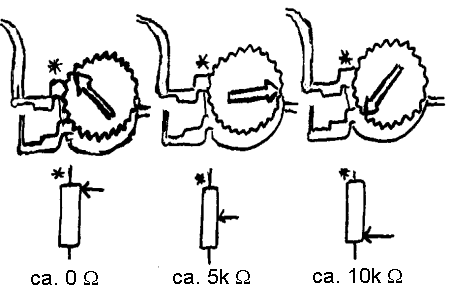
Hvordan resistansen bestemmer strømmen
Lag en enkel lysdimmer ved å koble opp kretsen som
vist yil høyre. Om vi vrir på den variable motstanden så vil lyset
fra lysdioden endre seg.
Forklaring Når vi skal forklarer det som skjer i elektriske strømkretser har vi tre ulike ord eller begrep som kan brukes. Disse er strøm (benevning: mA), spenning (benevning: V) og resistans (benevning: W). Siden alle disse begrepene er avhengige av hverandre er det vanskelig å lære om ett begrep av gangen. Denne strømkretsen viser da at en endring av resistansen i en strømkrets vil medføre endring i strøm og spenning. Følgende sammenheng mellom resistans og strøm gjelder alltid:
| Når vi øker resistansen i en krets, vil strømmen avta |
Noen typiske tallverdier
Når vi prøver å forstå
virkemåten til en strømkrets er det nyttig å vite litt
om hvor mye strøm og hvor stor resistans det er snakk om i konkrete
tilfeller. Den som arbeider litt med elektronikk har vanligvis et eget
multimeter slik at han kan måle strøm, spenning og motstand
selv. For de som ikke har tilgang på et multimeter vil vi her kort
nevne noen tallverdier. Grunnen er ikke at du skal huske verdiene, men
at du skal få en "føling" med hva slags tallverdier det er
snakk om i ulike strømkretser. Om du skal forstå de strømkretsene
som følger er det altså ikke nok å vite om det går
strøm eller ikke. Vi bør også ha en "føling
med" hvor mye strøm de ulike motstandene slipper gjennom. Strømmen
vil ellers variere litt med ulike batteri og lysdioder og tallene under
gir da bare en omtrentlig verdi. En lysdioden har også en resistans,
men fordi denne er relativt liten og ikke er fast, er det vanlig å
se bort fra denne.
Når variabel motstand har minst resistans
(100Ω) får
vi:
-Resistansen i hele kretsen: 430Ω
-Strømmen i kretsen: 4mA
Når variabel motstand har mest resistans
(10000Ω) får
vi:
-Resistansen i hele kretsen: 10430Ω
-Strømmen i kretsen: 0,4mA.
Seriekobling
Seriekobling av resistanser Som du kanskje ser
av koblingsskjemaet ovenfor så er totalresistansen i en krets lik
summen av resistansene i hver av komponentene. Men dette gjelder da bare
når komponentene er koblet i serie. Nå er det ikke bare resistanser
vi kan koble i serie, og her vil vi først gi en generell definisjon
av seriekobling:
| Komponenter er koblet i serie når de er koblet etter hverandre slik at den samme strømmen går gjennom alle komponentene. |
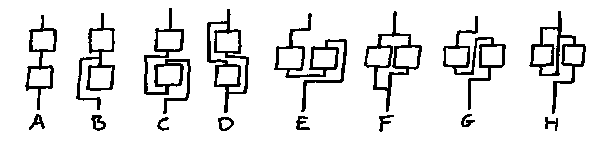
| Når motstander er seriekoblet finner vi totalresistansen ved å summere resistansen til hver av motstandene |
Dette er en nyttig regel som gjør at vi kan finne resistanser uten å bruke multimeter. Vi har for eksempel brukt denne i eksemplet ovenfor.
Lange ledninger betyr større resistans og mindre strøm. Prinsippet om at totalresistansen er lik summen av enkeltresistanser gjelder også for ledninger og det forklarer da hvorfor det er problemer med å føre strøm gjennom lange ledninger. I dette heftet antar vi at resistansen i de ledningene vi brukter er 0Ω, men dette er ikke helt riktig. Egentlig er det en liten resistans i alle ledninger, men om disse er korte er denne så liten at vi kan se bort fra denne. Men om vi f.eks. ønsker å føre strøm gjennom de tynne telefonledningene vi bruker her fra et hus til et annet vil vi fort oppdage at det blir lite strøm i ledningene. Også i en ledning på f.eks. 10 cm er det en liten resistans selv om vi ikke kan merke den. En ledning på 20cm vil da ha en resistans som er dobbelt så stor siden den er "to seriekoblede ledninger på 10 cm". Fortsatt er resistansen så liten at vi ikke merker den, men en ledning på f.eks. 100 meter er da 1000 ganger så lang som den som er 10 cm og det betyr da at denne har 1000 ganger så stor resistans. Om vi skal sende strøm over lange avstander bruker vi vanligvis tykke kobberledninger fordi resistansen er mindre i tykke ledninger enn i tynne ledninger.
Den største motstandene bestemmer strømmengden
i en krets
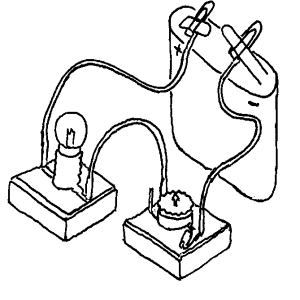
Hvis vi erstatter lysdioden med ei pære
slik som vist på figuren så får vi lite lys, selv om
vi skrur den variable motstanden på "maks". Hvorfor? Ei lyspære
trenger relativt mye strøm for å lyse og derfor har den liten
indre resistans (80Ω).
Men om det er andre motstander i kretsen så vil disse kunne hindre
at det går mye strøm, og det er da årsaken til at lyspæra
nesten ikke lyser. Den variable motstanden i elektronikkpuslespillet har
en sikkerhetsmotstand på 100Ω,
og vi får da en totalresistans på 180Ω
(80Ω+100Ω).
Dette gir en maksimal strøm omkring 22mA (I=U/R=4V/180Ω=22mA).
Til sammenlikning kan vi nevne at ei vanlig pære som er beregnet
på et 4,5V batteri har en indre motstand omkring 20Ω
og strømmen i ei vanlig lommelykt blir da omkring 200mA (I=U/R=4V/20Ω=200mA).
Merk 1: Den pæra vi bruker i elektronikkpuslespillet har spesiell stor resistans fordi vi senere skal koble den sammen med en transistor. De transistorene vi bruker tåler maksimalt 100mA. Om vi kobler denne pæra direkte til batteriet vil strømmen bli ca. 50mA (I=U/R=4V/80Ω=50mA)
Merk 2: Den variable motstanden vi bruker tåler ikke mye strøm. Hvis vi koblet ut sikkerhetsmotstanden på 100Ω så kunne vi fått pæra til å lyse maksimalt, men sannsynligheten er da stor for at motstandsbelegget i den variable motstanden blir ødelagt. Vi skal senere vise hvordan vi kan lage en lysdemper ved hjelp av den variable motstanden og lyspæra hvis vi i tillegg bruker en transistor.
Konklusjon: På samme måte som den svakeste lenken bestemmer styrken til et kjede, så kan vi si at den største motstanden i en seriekoblet strømkrets har mest innvirkning på strømmengden i kretsen.
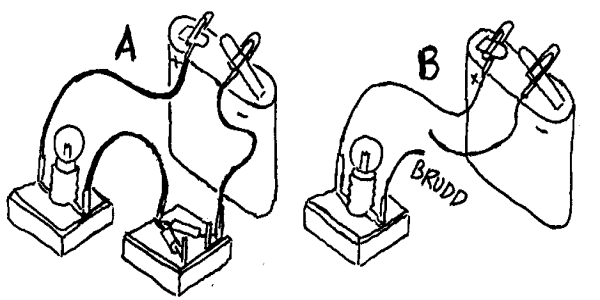
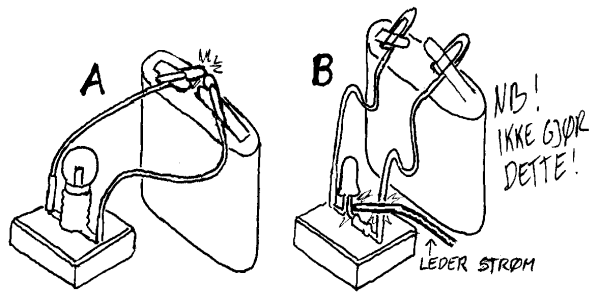
Strømbrudd
Strømbrudd er i prinsippet det samme som
om vi setter inn en motstand i kretsen som har for stor resistans. Pæra
til venstre lyser ikke ved for stor motstand(A) og ved brudd(B) (men batteriet
tappes ulikt mye)
Kortslutning
En kortslutning er egentlig en strømkrets
med for liten resistans. I praksis er det ingen som ønsker å
lage slike strømkretser, men det kan da oppstå feil som gjør
at strømmen tar snarveier som ikke var meningen. Generelt er det
slik at elektronstrømmen velger "minste motstands vei" fra minuspolen
til plusspolen. Det er da vår oppgave å passe på at det
ikke oppstår snarveier utenom komponentene. Hensikten med motstandene
er f.eks. å redusere strømmengden til et passende nivå.
Men hvis elektronene "ser" at det finnes snarveier til plusspolen utenom
"de anviste rutene" så startes det et "stormløp" som kan få
uheldige konsekvenser.
Figuren viser eksempler på kortslutninger:
I tilfelle A går strømmen direkte mellom bindersene i stedet
for å gå gjennom lyspæra. I tilfelle B går strømmen
utenom motstanden og lysdioden vil få for mye strøm slik at
den ødelegges.
Tidligere har vi lært at strømmen i en strømkrets øker når resistansen avtar. Om vi så har en strømkrets med en resistans nær 0Ω vil strømmen bli svært stor. En kortslutning er uheldig av flere grunner:
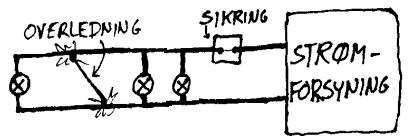
Hvordan sikre seg mot ødeleggende feil
For å unngå slike skadevirkninger
som er nevnt ovenfor bruker vi sikringer i ulike sammenhenger. Ei sikring
er ofte en leder som "brenner opp" om det går mer strøm enn
det den er beregnet for. (En sikring kan også være en mekanisme
som automatisk reduserer strømmen om denne blir for stor.) Når
sikringen går, vil strømmen brytes og dette hindrer da at
andre mer kostbare komponenter skal ødelegges eller at ledninger
skal bli varme og starte brann. Sikringen hindrer både at ledninger/komponenter
går varme og at strømforsyningen skal overbelastes.
Kortslutningsvarsel
Når det skjer brudd i strømkretsene
vil det vanligvis ikke skje noe galt mens vi leter etter feilen. Når
det derimot skjer en kortslutning, er det viktig at vi får stoppet
den før vi kjenner eller lukter varmen. Et batteri tappes fort ut
om det kortsluttes.
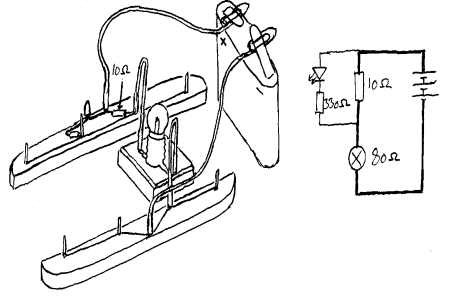
Elektronikkpuslespillet inneholder to strømdelere
som har til hensikt å gjøre tilkoblingen av ulike komponenter
enkle og oversiktlige. På strømdeleren som skal kobles til
den positive polen på batteriet finnes det da en lysdiode som lyser
om det skjer en kortslutning eller overbelastning. Denne kan du prøve
ved å koble opp følgende:
Koblingskjemaet viser da at strømmen går gjennom en motstand på 10Ω i tillegg til lyspæra som har en resistans på ca 80Ω. Det betyr at vi taper litt lys i forhold til om vi ikke hadde hatt motstanden på 10Ω. I praksis vil spenningen over lyspæra bli litt mindre enn den hadde vært uten motstanden, men denne spenningsreduksjonen er så liten at vi fortsatt kan regne med at vi har ca 4V over lyspæra. Det vi tjener på å sette inn denne motstanden er da følgende:
Testing av kortslutningsvarsleren
1) En direkteledning mellom strømdelerne
betyr kortslutning og lysdioden vil lyse. Om kortslutningen varer for lenge
vil motstanden på 10Ω
bli varm og kanskje bli ødelagt. Denne motstanden fungerer derfor
også som en slags sikring.
2) Om vi bytter ut pæra med ei på
0,3A (vanlig i lommelykter) vil strømmen bli så stor at lysdioden
lyser litt hele tiden. Det er da ikke snakk om kortslutning, men den røde lysdioden
varsler da om at strømmen er mer enn ca. 150mA. Det er nyttig å
få et slikt varsel fordi det da er en fare for at noen komponenter
kan bli ødelagt (transistorer ol).
Merk at den røde lysdioden ofte gi et lite
blink idé vi kobler til ei lyspære. Dette viser da at resistansen
i glødetråden er vesentlig mindre før den blir varm.
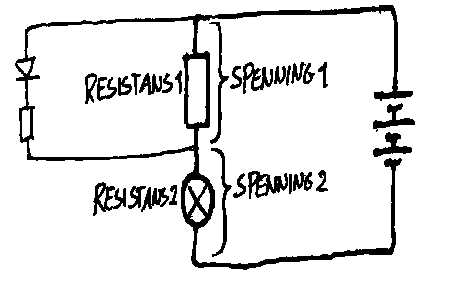
Virkemåten til kortslutningsvarsleren Betingelsen for at den røde lysdioden skal lyse er som nevnt tidligere at den får tilført en spenning over 1,5V. I skjemaet nedenfor betyr det at Spenning 1 1,5V. Hoveddelen av strømmen går gjennom motstanden på 10Ω og lyspæra og disse vil da fordele spenningen på 4V mellom seg. Forholdet blir da som forholdet mellom resistansene:
Lyspære med resistans 80Ω:
Resistans 1: 10Ω
(er 11% av 90Ω)
Spenning 1: 0,4V (er 11% av 4V)
Resistans 2: 80Ω
(er 89% av 90Ω)
Spenning 2: 3,6V (er 89% av 4V)
Totalresistans: 90Ω
Totalspenning: 4V
(Strøm:I=U/R=4V/90Ω=40mA)
Konklusjon: 0,4V er for lite til at lysdioden
vil lyse
Lyspære med resistans 15Ω:
Resistans 1: 10Ω(er
40% av 25Ω) Spenning
1: 1,6V (er 40% av 4V)
Resistans 2: 15Ω
(er 60% av 25Ω)
Spenning 2: 2,4V (er 60% av 4V)
Totalresistans: 25Ω
Totalspenning: 4V
(Strøm:I=U/R=4V/25Ω=160mA)
Konklusjon: 1,6V er nok til at lysdioden vil
lyse
Sammenheng mellom resistans og spenning
Talleksempelet foran viser at
det er en sammenheng mellom resistans og spenning. Her vil vi lage en huskeregel
som er nyttig når vi senere skal finne spenningen ulike steder i
en krets.
| Når motstander er koblet i serie, vil vi få stor spenning der det er stor resistans og liten spenning der det er liten resistans. |
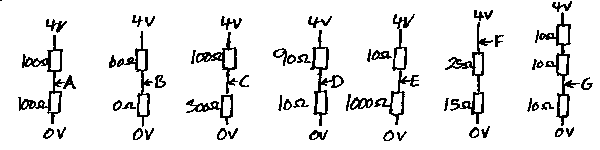
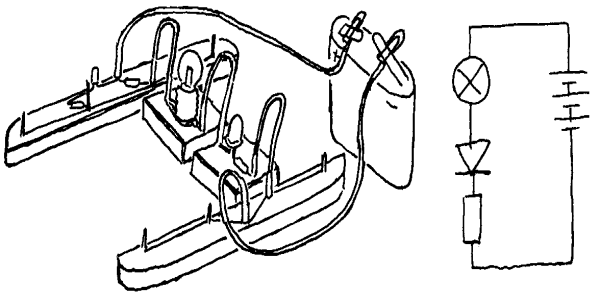
Husk at det er summen av resistansene som bestemmer hvor mye strøm det går gjennom en seriekobling. Regelen her sier da at det er forholdet mellom de ulike resistansene som bestemmer hva spenningen blir på ulike steder i kretsen. Vanligvis er det ikke så viktig å vite nøyaktig hva spenningen er. Derfor bruker vi ikke tid på å vise hvordan vi kan beregne spenningen matematisk. Det viktigste er at vi kan anslå hva spenningen er ulike steder. Figuren viser noen eksempler på seriekopling med noen enkle tall, og om du klarer å anslå hva spenningen er ved de ulike bokstavene, så har du forstått prinsippet.
Forsøk som illustererer spenningsdeling
Kobl opp kretsen som er vist på figur.
Hvorfor lyser ikke pæra?
Anslå totalresistans, strøm og spenningen
i A
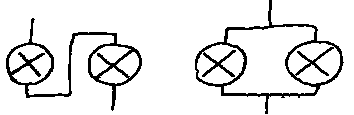
Når strømmen deler seg
Ofte lar vi en spenningskilde (batteri) sørge for strøm
til mange ulike komponenter. I prinsippet finnes det to måter å
koble komponenter til en spenningskilde. Den ene måten kalles seriekobling
og den har vi definert tidligere i dette heftet. Den andre måten
kalles parallellkobling.
| Komponenter er koblet parallelt om tilført strøm deles opp før den går gjennom komponentene |
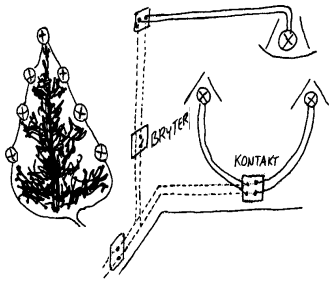
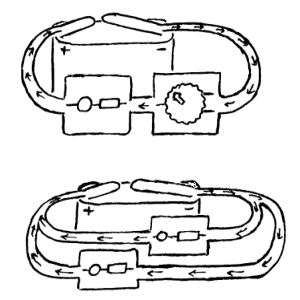
Nå er det lettere å forklare forskjellen mellom seriekobling og parallellkobling ved å bruke figurer enn ved å bruke ord. Koblingskjemaet ovenfor viser da to seriekoblede og to parallellkoblede lyspærer. Utfra dette skjemaet kan vi si at de parallellkoblede pærene har samme spenning mens de seriekoblede pærene har samme strøm. Videre er det slik at hvis den ene av en serie med seriekoblede pærer skrues ut, så vil alle pærene slukne. Lysene på et juletre er et eksempel på en slik seriekobling. Hvis vi derimot skrur ut en av mange parallellkoblede pærer, så er det bare denne ene pæra som slukner. Lyspærene i hjemmet er da et eksempel på en slik parallellkobling.
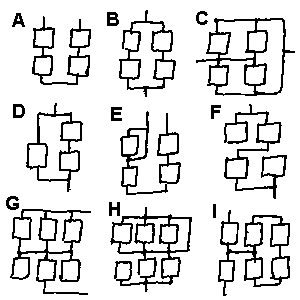
En elektrisk krets består vanligvis av en kombinasjon av parallellkoblinger og seriekoblinger. Figuren til høyre viser noen kretser og om du klarer å si hvor det er seriekoblinger, hvor det er parallellkoblinger og hvor det er en kombinasjon av disse, så har du sannsynligvis forstått hva som menes med seriekobling og parallellkobling. Skriv gjerne S(seriekobling), P(parallellkobling) eller K(kombinasjon av begge deler) ved skjemaene. Sett gjerne også kryss over de komponentene som ikke får strøm.
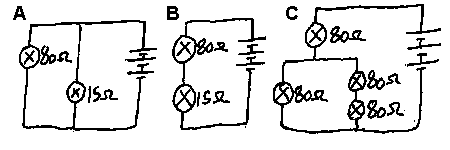
Det viktigste i forbindelse med begrepene seriekobling og parallellkobling er ikke å kjenne dem igjen når man ser dem, men heller å huske hvordan de ulike koblingstypene påvirker strøm og spenning. Kan du f.eks. si hvilke pære som vil lyse mest og minst i det tre tilfellene som er vist til høyre.
Brytere
Hensikten med en bryter er å koble strøm til og fra komponenter
eller elektrisk utstyr. Det skjer vanligvis ved at en strømleder
brytes eller kobles sammen (enkel bryter). (Senere skal vi da se at også
en transistor kan fungere som en bryter.) I noen tilfeller blir begge strømlederne
mellom spenningskilden og det elektriske utstyret brutt i en bryter (dobbel
bryter). En bryter kan også koble strømmen over fra en komponent
til en annen (vekslingsbryter). Figuren viser symboler for enkel bryter,
dobbel bryter og toveis vekslingsbryter.
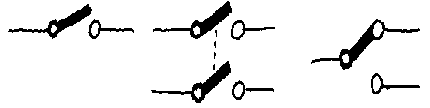
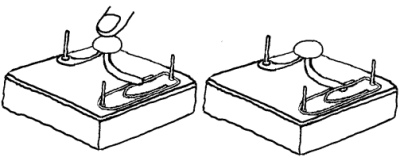
Her vil vi konsentrere oss om de bryterne som bryter/kobler sammen
en leder. Selv om vi bruker samme symbol på dem, så kan de
fungere på to ulike måter. I en vanlig lysbryter kobler vi
til strømmen i ett trykk og fra strømmen i et nytt trykk.
Denne bryteren er altså stabil i både 'på' og 'av'-posisjonen
og her kaller vi den bistabil bryter. I navnet ligger det at den er stabil
i to ('bi') posisjoner. Bryteren til en ringeklokke leder derimot bare
strøm så lenge man trykker på den. Denne bryteren er
da bare stabil i 'av'-posisjonen. Denne bryteren kan vi da kalle monostabil
bryter fordi den bare har en ('mono') stabil stilling. Den forenklede bryteren
som er laget av en splittbinders og en vanlig binders fungerer da som både
bistabil bryter og monostabil bryter.
Brytere skal alltid seriekobles. Når en bryter er seriekoblet
med det som skal ha strømmen vil den da bryte strømmen når
vi slår den av slik hensikten var. Om vi derimot kobler en bryter
parallelt med en komponent, vil bryteren representere "minste motstands
vei" og stjele all strømmen fra komponenten. Det blir med andre
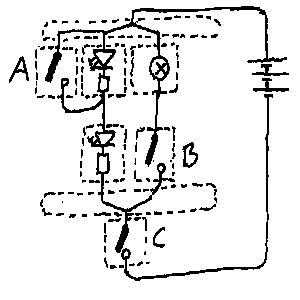
ord en kortslutning. Vi kan ha mange brytere i elektrisk utstyr. Den bryteren
som da kobler ut all strømmen kalles da hovedbryter. I figuren har
vi en parallellkoblet bryter (ikke skadelig slik den er koblet her), en
seriekoblet bryter og en hovedbryter. Forklar hva som skjer når de
ulike bryterne slåes av og på. Kobl gjerne opp kretsen som
er vist her og sjekk om du tenker rett. Om du mangler brytere så
er det mulig å bruke to ledningsender og en løs stift som
bryter.
1 Bruke lysdiode + batteri og finn betingelsen for at lysdioden skal lyse. (koble + til +) NB: Kobl ledninger kun til stiftene, ikke mellom lysdiode og motstand da dette vil medføre at lysdioden ødelegges.
2 Prøv variabel motstand (potensiometer) sammen med komponentene ovenfor (i en seriekobling) og spør elevene om når det går mye og lite strøm.
3 Kobl inn lysfølsom motstand i stedet for variabel motstand (potensiometer) og trekk konklusjoner. Hvorfor kan ikke lysdioden styre summer og lyspære direkte?
4 Introduser strømdelerne og fortell hensikten med disse. (advare mot overledning og gjøre koblinger mer oversiktlig)
5 La elevene leke litt med å koble ulike ting mellom strømdelerne. Det er ikke mulig å ødelegge komponenter om man kun kobler ledningene til stiftene.
Viktige begrep
Strøm: Elektrisk strøm er mange elektroner som beveger seg i samme retning (fra - til +). Symbol: I Benevning: A (ampere)
Seriekobling: Når samme strøm går gjennom to eller flere komponenter kalles det seriekobling.
Parallellkobling: Når strømmen deler seg før den går gjennom komponenter, sier vi at komponentene er parallellkoblet.
Resistans: Komponenter og ledninger kan ha stor eller liten resistans. Når resistansen er stor slippes lite eller ingen strøm gjennom (eks: 33kΩ -motstanden og kondensator). Når resistansen er liten slippes mye strøm gjennom (eks: ledninger og lyspære). Symbol: R Benevning: Ω (ohm)
Spenning: Elektrisk spenning er kraften som skyver/drar elektronene når vi har strøm. Ofte må spenningen til komponentene overskride en bestemt minimumsverdi (Umin) for at komponentene skal virke. En lysdioden vil f.eks. ikke lyse om spenningen er under 1,5V. Symbol: U Benevning: V (volt)
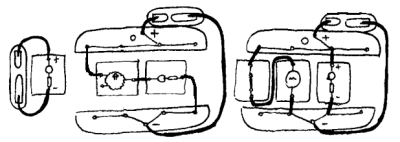
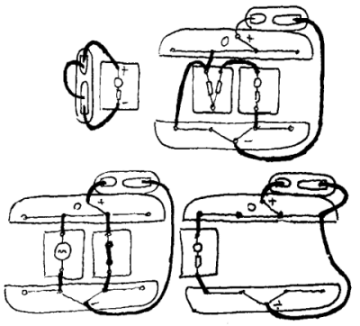
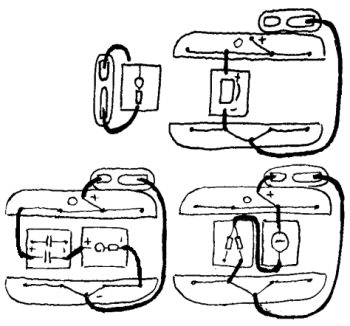
Eksempler:
1 For at det skal gå strøm må det være sammenhengende elektrisk kontakt fra - til + på batteriet. Dette kalles en strømkrets.
2 Om det finnes snarveier (ledere med liten resistans) som kan føre strømmen utenom komponenter kalles det kortslutning (eller overledning) og komponentene får da ikke strøm.
3 Komponentene virker ikke når de får for lite strøm. Årsaken til dette kan være brudd (manglende kontakt) i strømkretsen. Komponenter med stor resistans kan også forårsake at andre komponenter ikke virker (ved seriekobling).
Oppgaver
Spørsmål til ettertanke
1 Hvor mye vil du anslå at du har lært
om elektrisk strøm når du:
- Husker definisjonen av strøm.
- Husker alt som står i boka.
- Kan koble opp alle strømkretsene som
står i boka.
- Når du kan forklare hva som skjer i en
ny strømkrets.
- Kan lage nye nyttige strømkretser som
ikke står i boka.
- Kan finne feil i strømkretser og reparere disse.
(gradering fra f.eks. 0 til 10)
Oppgaver som tester forståelsen
2 Lysdioden, lyspæra og summeren trenger
ulik mengde strøm. Beskriv forsøk som viser hvilke som trenger
mest og minst strøm.
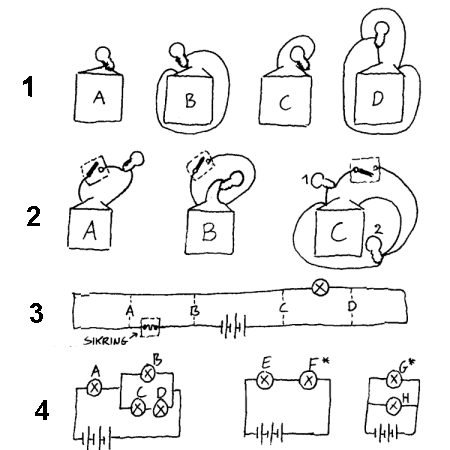
3 Hvor mange seriekoblede lysdioder kan lyse ved en spenning på 4V?
4 Bør en lysdiode kobles før eller etter en lysdiode?
5 Vil en grønn lysdiode lyse om vi kobler den til et 1,5V batteri?
6 Når lyser lyspæra i figur 1?
7 Hva skjer når vi trykker på bryteren i figur 2?
8 Hva skjer om det blir overledning/kortslutning ved A, B, C og D i figur 3?
9 Hvilke lyspærer lyser mest og minst i de kretsene i figur 4? (F har mindre resistans enn de andre pærene)
10 Tegn et koblingsskjema for en strømkrets med to lyspærer som styres av hver sin bryter, og en hovedbryter som slukker alle pærene.
11 Svar kort på oppgavene med stikkord.
Begrunnelser/utfyllende kommentarer skrives i en parentes.
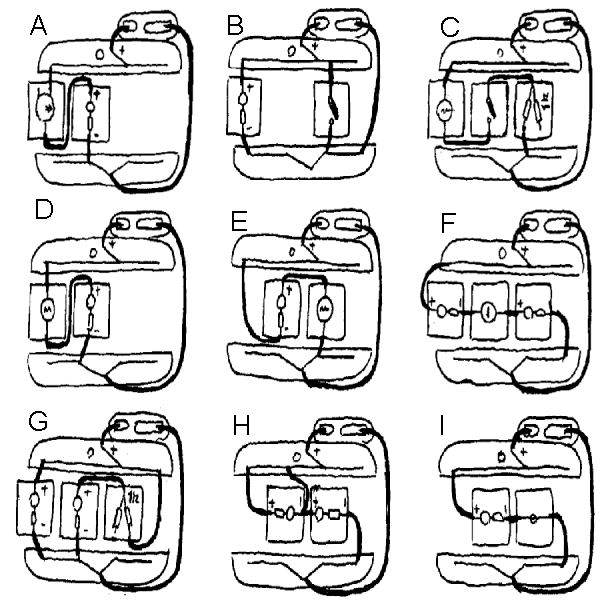
Eksempel:
A: Vil lysdioden lyse? Svar: Ja (Mest ved liten
resistans)
B: Når lyser lysdioden? Svar: Når
bryteren er av (Kortslutning ellers)
C: Når lyser pæra?Svar: Aldri (For
stor motstand)
Enkle koblinger:
D: Vil lysdioden lyse?
E: Vil lysdioden lyse?
F: Hvilke lysdiode lyser mest?
G: Hvilke lysdiode lyser mest?
H: Vil lysdiodene lyse?
I: Når lyser lysdioden?
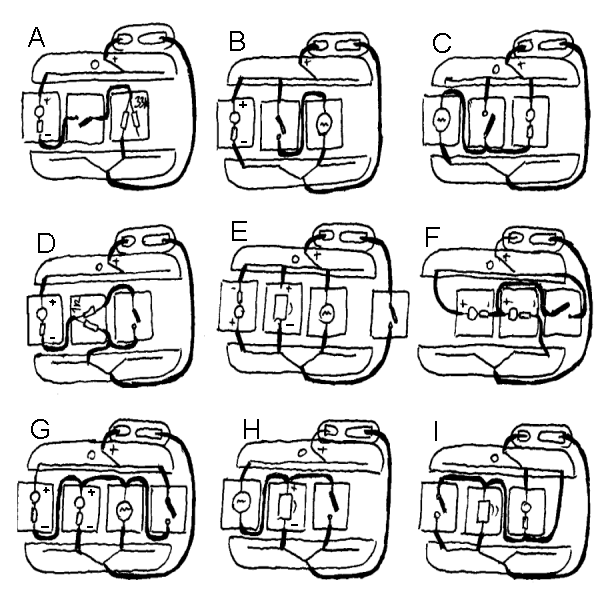
12 Oppgaver med bryterkoblinger:
A: Når lyser lysdioden?
B: Hva skjer ved på/av?
C: Hva skjer ved på/av?
D: Hva skjer ved på/av?
E: Hva skjer ved på/av?
F: Hva skjer ved på/av?
G: Hva skjer ved på/av?
H: Hva skjer ved på/av?
i: Hva skjer ved på/av?
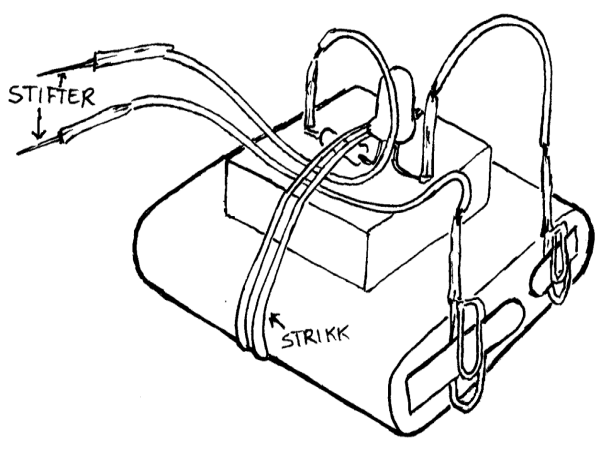
Lag en ledningsevnetester Når det oppstår feil i elektrisk utstyr, skyldes dette ofte strømbrudd. Her følger en nyttig tester som kan brukes for å finne strømbrudd i tillegg til at den også kan teste ledningsevne i ulike stoff. Bruk to ubrukte stifter i enden på ledningene og et strikk for å holde instrumentet sammen.
Brukeropplæring Når vi skal bruke et måleinstrument trenger vi vanligvis en brukeropplæring for at resultatet av målingene våre skal bli pålitelig. Her følger noen nyttige tips:

Nå er det vanlig å snakke om gode og dårlige ledere, og ved hjelp av testeren som er vist her kan vi skille mellom disse. Om lysdioden lyser mye når vi tester stoffet sier vi da at vi har en god leder. I skjemaet nedenfor kan vi markere det med stor 'L'. Om lysdioden lyser lite, sier vi da at vi har en dårlig ledere og vi skriver da en liten 'l' i skjemaet nedenfor. Om lysdioden ikke lyser sier vi da at vi har en isolator og vi skriver da bokstaven 'i' i skjemaet. Merk at det også finnes gode og dårlige isolatorere og senere skal vi lage et instrument som kan skille mellom disse. Figuren viser hvordan man teste en væske, en motstand og en blyant.
Finne ledningsevnen i ulike stoff Ledningsevnetesteren til å sjekke de tingene/stoffene som er nevnt i tabellen nedenfor leder strøm. Føy selv til nye ting/stoff.
| Ting/stoff | L/l/i | Ting/stoff | L/l/i |
| En nøkkel | Luft | ||
| Trebit | Stein | ||
| Papir | Appelsin | ||
| Blyantbly (grafitt) | Rent vann | ||
| Plast | Saltvann | ||
| Hud/fingrer | Saft | ||
| Melk | |||
Noen konklusjoner om ledere og isolatorer Etter at ledningsevnen i ulike stoff er undersøkt, er det naturlig å prøve å trekke noen konklusjoner. Her vil vi da nevne noen generelle konklusjoner som eventuelt kan brukes for å kontrollere egne data. Generelt er metaller gode ledere, og i ledninger bruker man da oftest kopper. Det som kjennetegner gode ledere er at de har mange bevegelige elektron. På den andre siden er plast, gummi, glass, luft ol. dårlige ledere og disse brukes da ofte som isolasjon rundt elektriske ledninger. Andre stoff vil da lede strøm mer eller mindre. En generell regel er da at fuktighet (tilstedeværelse av vann) gjør mange stoff ledende. Et eksempel er kjøkkensalt. Tørre saltkorn leder ikke strøm, men når det blandes ut i vann leder det strøm. Generelt kan vi si at jo fuktigere et stoff er, jo bedre leder det strøm. Til vanlig regner vi ikke rent vann som en leder men som vi senere skal se er vann heller ikke en god isolator. Her vil vi derfor kalle rent vann, hud ol. for dårlige isolatorer.
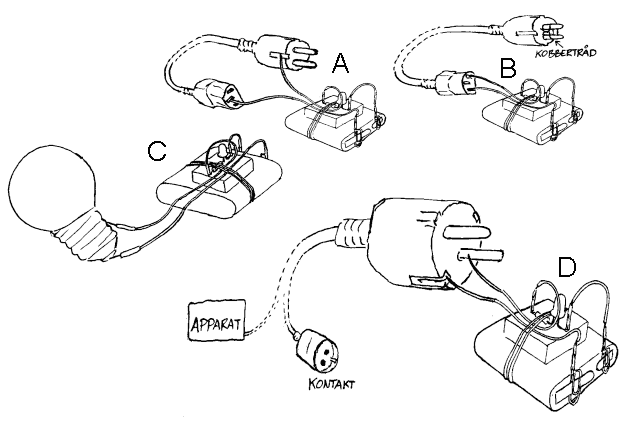
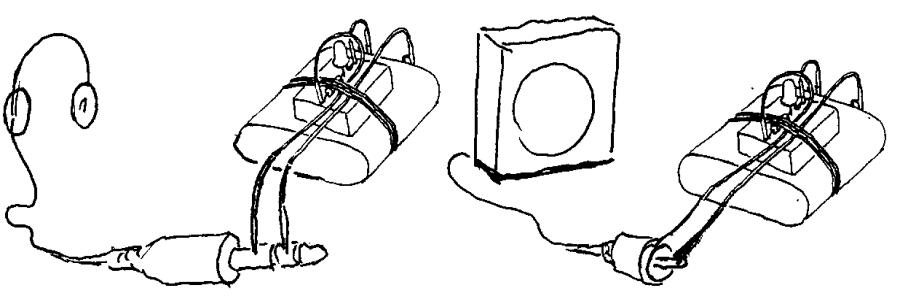
Teste høytalere, datakabler oa.
Den ovennevnte testeren kan også brukes til å teste om høytalere
er ok, om datakabler er ok eller om man rett og slett ønsker å
finne ut hvilke ledere som hører sammen i to ender av en kabel.
Den kan videre brukes til å finne brudd i koblingsbrett og andre
elektriske instrument, men dette vil vi komme tilbake til når det
er aktuelt. Her vil vi bare oppsummere med å si at en leder som er
beregnet på å lede mye strøm også kan lede lite
strøm. Strømmen gjennom lysdioden vår er på ca.
8mA og denne lille strømmen vil da ikke ødelegge utstyr som
er beregnet på mye større strømmer. Merk ellers at
andre strømkilder må kobles ut før man bruker testeren
som er vist her. Her vil vi til slutt oppfordre leseren til å tenke
ut andre anvendelser av den enkle testeren som vi har laget her.
Hvis lysdioden
lyser og det kommer lyd fra høytaler i figuren vet vi at høytaleren
er i orden og eventuelle feil finnes da sannsynligvis i forsterker eller
andre steder.
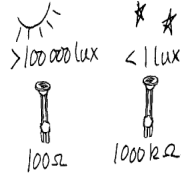
Lag en lysmåler
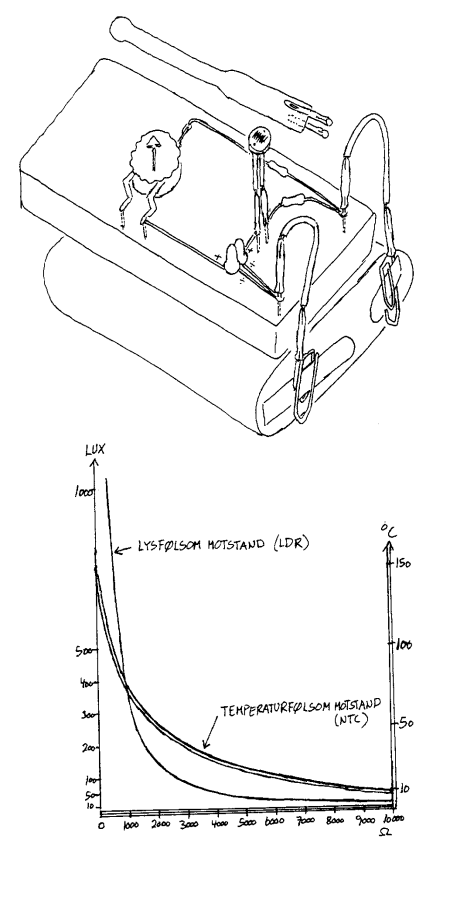
I elektronikkpuslespillet finnes det en lysfølsom motstand (og
en temperaturfølsom motstand) som endrer motstanden i forhold til
det lyset som treffer den. Her vil vi vise hvordan vi kan bruke denne for
å finne en lux-verdi for det lyset som omgir oss. Lux er enheten
for lysinnstråling. Den lysfølsomme motstanden har en resistans
omkring 100Ω i solskinn
og omkring 1000 kΩ
(=1 000 000 Ω) i
mørke. Dette svarer da til en lysstyrke på mer enn 100000
lux om dagen og mindre enn 1 lux i måneskinn.
Nå er øynene våre dårlig
til å anslå hvor mye lys det er i ulike situasjoner. Årsaken
er at øynene er konstruert for å se både når det
er mye lys om dagen og når det er lite lys om natten. Det finnes
altså prosesser i øyet vårt som tilpasser seg etter
hvor mye lys det er, og hjernen som da mottar synsintrykkene vil da ikke
oppdage at det er så mye forskjell på dagslys og "nattlys"
som det virkelig er. Den lysfølsomme motstanden derimot vil ha en
resistans som har et direkte forhold til det lyset som treffer den. I elektronikkpuslespillet
finnes det ikke noe som kan vise luxverdien direkte, og derfor vil vi her
utnytte en øynene våre på et område hvor de gir
pålitelige data. Selv om øynene ikke er flinke til å
bestemme absolutt lysstyrke så er de ganske flinke til å avgjøre
hva som lyser mest når lyskilder befinner seg nær hverandre.
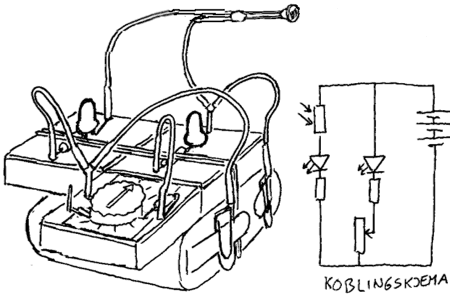
Ved hjelp av elektronikkpuslespillet kan vi lage lysmåleren som er
vist til høyre.
Forklaring av virkemåten Kretsen er en parallellkobling hvor strømmen sprer seg til to like lysdioder med samme farge. Når lysdiodene lyser like sterkt vet vi at det går like mye strøm gjennom dem. Det er da en lysfølsom motstand (LDR) og en variabel motstand som bestemmer hvor mye strøm det skal gå gjennom de to lysdiodene. Når vi bruker den som lysmåler vil lyset bestemme strømmen i den ene lysdioden og så stiller vi inn lyset i den andre lysdioden slik at de lyser like mye. Pilen på den variable motstanden vil da peke på en lux-verdi. For å lettere avgjøre når lysdiodene lyser like mye, kan det være lurt å snu disse vekk fra lyskilden og det kan også være lurt å lage en skjerm som hindrer at lyset fra lyskilden treffer lysdiodene.
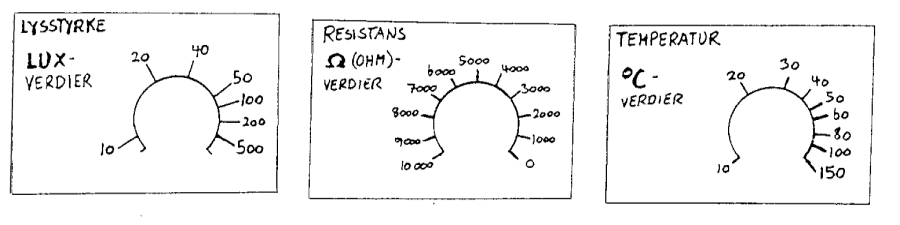
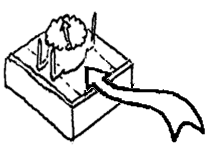
Kalibrering av lysmåleren Kalibrering betyr at vi lager en rett skala på et måleinstrument. I dette tilfellet betyr det at vi må bruke et ferdig kalibrert luxmeter og måle lyset som treffer måleinstrumentet vårt. Der som pila til potensiometeret peker skriver vi da denne lux-verdien. Vi gjør så det samme for ulike lux-verdier og resultatet blir da en skala som er vist over. Nå er det ikke så mange som har et luxmeter og meningen her er at man kopierer skalaen under og plasserer den under den variable motstanden. Merk at du må bruke den endekontakten på den variable motstanden som er nærmest de høye lux-verdiene, ellers vil skalaen gå feil vei.
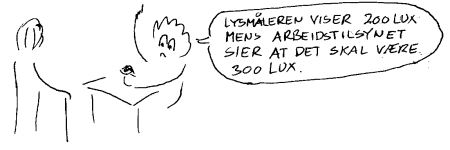
Bruksområde og sammenlikningsverdier
Merk at det her er mange ulike feilkilder og du må ikke stole for
mye på denne enkle lysmåleren. Det gjelder spesielt ved store
lux-verdier hvor skalaen er svært tett. For at du skal ha noe å
sammenlikne egne verdier med, så vil vi her oppgi noen lux-verdier
som anbefales av Selskap for Lyskultur og som da brukes av Statens Arbeidstilsyn.
| Villagater/småveier 2-4 | Korridorer 80 |
| Gater med stor trafikk 6-10 | Vanlige oppholdsrom 150 |
| Byggeplasser 40-80 | Leserom/klasserom 300 |
| Formingsrom 500 |
Tabell over egne lysstyrkeverdier
| Beskrivelse | Luxverdi |
| I klasserommet på pulten | |
| I en korridor | |
| Ute i solskinn | |
| En solskinnsdag i en tett skog | |
| Ute en dag det regner | |
| I vinduet tidlig på morgenen | |
| I vinduet kl. 1300 | |
| Hjemme i stua om kvelden | |
Her vil vi da beskrive og forklare noen enkle transistorkretser som kan lages ved hjelp av elektronikkpuslespillet. Det er da viktig at leseren hele tiden prøver å forstå hva som skjer i de ulike kretsene, og ikke bare gjør aktivitetene for å se hva som skjer. Mål for dette kapitlet er:
Forståelse for hvordan transistoren kan brukes som bryter og forsterker i ulike sammenhenger.
I tillegg til de komponentene fra elektronikkpuslespillet som var nevnt i forrige kapittel trenger man her to transistorer, en summer og en kondensatorbrikke.
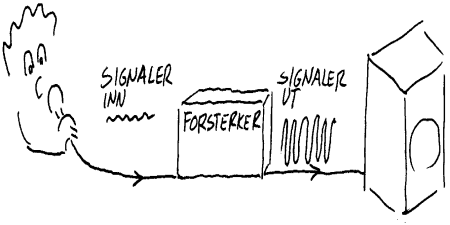
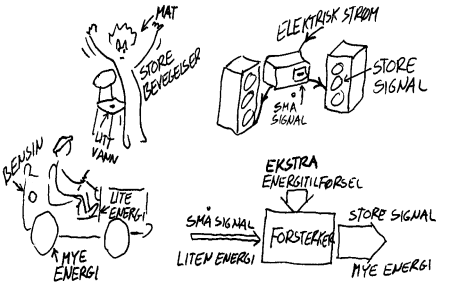
Ordet forsterke betyr at noe blir sterkere. I en forsterker vil da innsignalene fra en mikrofon være svaker enn utsignalene til en høytaler. De svake signalene som kommer fra mikrofonen vil med andre ord styre de sterke signalene som går til høytaleren. Energien ut av en forsterker er større enn energien som går inn på inngangen. Om vi tenker oss om er det ikke vanskelig å finne andre eksempler på slik forsterkning. I en bil vil f.eks. små krefter mot gasspedalen styre mye større krefter i drivhjulene. Også i oss mennesker skjer det slike forsterkningsprosesser. Gjennom sansene våre mottar vi relativt små signaler som i sin tur medfører at vi gjør ulike større handlinger. Felles for all slik forsterkning er at det er mer energi i utsignalene eller innsignalene og det trenges derfor en ekstra energitilførsel. Forsterkeren får energi via en elektrisk kontakt, bilen får energi fra bensintanken og vi mennesker får energi gjennom den maten vi spiser. Merk at der det skjer en forsterkning vil det alltid finnes en ekstra energitilførsel.
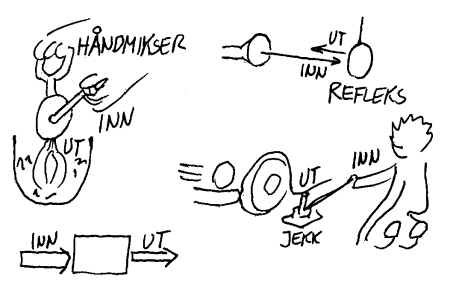
Eksempler hvor det ikke er snakk om forsterkning
For å virkelig forstå hva som menes med forsterkning er det også nyttig å kjenne eksempler på energiprosesser som ikke innebærer forsterkning. Et refleks er et eksempel på noe som mottar signal (lys) og så sender disse tilbake uten å forsterke. Reflekset bruker altså bare energien i tilført lys når den "lager" den lysstrålen som sendes tilbake. I en håndvisp tilfører hånden energi til sveiven og mikseren vil da omforme denne energien til en annen type bevegelse (raskere). I en biljekk tilføre vi energi til håndtaket, som så brukes til å hever bilen. Kraften som hever bilen er annerledes (større) enn den kraften vi tilfører jekken, men energien er den samme (eller litt mindre på grunn av friksjon). Det er altså ikke snakk om en energiforsterkning. I disse tilfellene er det altså mer eller mindre av tilført energi som vi får ut. Det skjer altså ikke en tilførsel av ekstra energi slik som i en forsterkning. Det betyr i praksis at signaler og annen energi vil bli svakere ved hver omforming. Energien ut blir altså mindre eller lik energien inn i disse tilfellene.
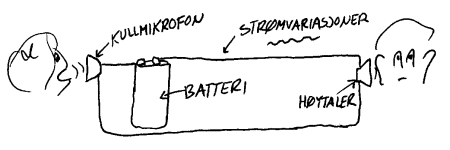
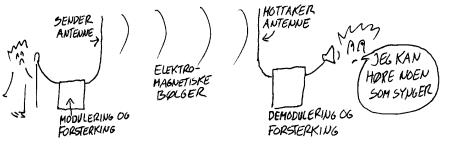
Når det gjelder elektrisk energi kan vi bruke den til lyspærer og elektromotorer uten å bruke forsterkere. Alle aktivitetene i hefte 1 er da eksempler på elektriske prosesser hvor det ikke skjer forsterkning. Det er f.eks. mulig å variere strømstyrken ved hjelp av variable motstander og signaloverføring ved hjelp av telefon var da mulig også uten forsterkning. Til høyre vises prinsippet for de første telefonene. I mikrofonen varierer resistansen som følge av trykkforandringer, og høytaleren beveger seg som følge av strømforandrindringer.
Radiorøret - den første elektriske forsterkeren
Før radiorøret ble oppfunnet var det klare grenser for hvor svake signaler man kunne måle eller påvise. Radiokommunikasjon skjer f.eks. via elektromagnetiske signal som er sterke ved senderen og svært svake ved mottakeren. Det trenges derfor en forsterking i radiosenderen som da omformer vanlig tale og musikk til sterke radiobølger. Ved mottakeren trenges det så en tilsvarende en forsterker som omgjør svake radiobølger til hørbar lyd i høytaleren. Radiorøret fungerer som en strømforsterker og oppfinnelsen av dette gjorde blant annet at man kunne måle eller påvise langt svakere signal enn tidligere. Her vil vi ikke gå inn på radiorørets virkemåte, men bare nevne at virkemåten har mye til felles med virkemåten til transistoren som da er tema for dette heftet. Det viktigste nye som fulgte etter radiorørets oppfinnelse var vel radioen og det er vel grunnen til at navnet 'radiorør'. Radiorøret er relativt sammensatt og komplisert og dessuten trenger det relativt mye energi for å virke. Det er nok grunnen til at det ikke ble så anvendelig som transistoren senere ble.

Transistoren - grunnlaget for moderne elektronikk
Transistoren ble oppfunnet i 1948, og det er da denne som er grunnlaget for moderne elektronikk. Den er billig å produsere, enkel å bruke og nyttig i mange ulike sammenhenger. I vårt moderne samfunn har vi gjort oss avhengig av elektronisk utstyr på de fleste områdene og derfor er det nyttig for folk flest å vite litt om virkemåten til det utstyret vi bruker til daglig. En forståelse for transistorens virkemåte vil sannsynligvis gjøre at vi bedre forstår mulighetene og begrensningene som ligger i moderne elektronisk utstyr. Generelt kan vi vel si at en grunnleggende forståelse for det utstyret vi bruker vil hjelpe oss med å styre teknologien i stedet for at teknologien styrer oss.
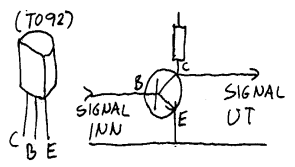
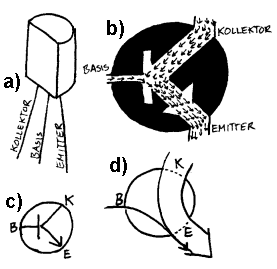
Transistoren kan brukes til forsterkning og det er da nyttig å tenke på den som en forsterker når du arbeider med dette heftet. En vanlig forsterker har da en inngang, en utgang og en ekstra energitilførsel som vist foran. En transistor har tre foter, og her vil vi da først understreke at det ikke er en direkte en-til-en-sammenheng mellom disse. Når vi skal overføre et elektrisk signal eller elektrisk energi trenger vi to ledere som nevnt tidligere. Inngangen på transistoren er da fotene som har fått navn B (basis) og E (emittere). Det er videre en felles utgang og energitilførsel som da er knyttet til fotene som kalles C (kollektor) og E (emittor). Bokstavene er vanlig i internasjonal litteratur. Selve navnene har en historisk bakgrunn og for å unngå unødvendig forvirring vil vi i dette heftet kun bruke de tre bokstavene. Emittoren (E) er da felles for inngangen og utgangen og i praksis vil signalene på de to andre variere i forhold til denne som da får en slags stilling som en passiv referanse. Bokstaven E står alene i alfabetet mens de to andre B og C er naboer og her vil vi da bruke dette som en slags huskeregel. I en forenklet og litt upresis forklaring sier vi da at signalet går inn på B (første bokstav) og går ut på C (etterfølgende bokstav).
Hvis vi skal prøve å formulere en huskeregel som sier noe kort om hva en transistor gjør så kan det f.eks. bli som følger:
I en transistor vil en liten strøm gjennom B styre en mye større strøm gjennom C-E. |
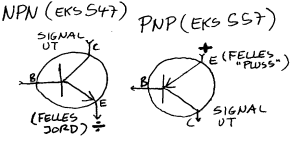
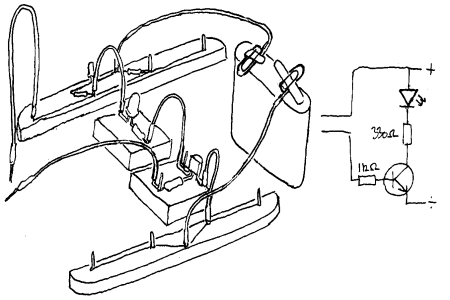
I transistorene vi foreløpig bruker i elektronikkpuslespillet (BC547B) vil C-strømmen være 200-450 ganger større enn B strømmen. I dette hefte vil vi da for enkelhet skyld si at en slik transistor gir en strømforsterkning på 300 ganger. Videre finnes det to typer transistorene (NPN og PNP) og det som skiller disse fra hverandre er da om elektronene går ut eller inn på B. 547-transistorene er NPN transistorer og her går elektronene ved normal bruk ut av B.
En enkel strømforsterking
Kobl opp kretsen som er vist til høyre. Lysdioden skal da lyse om du f.eks. holder på de to løse ledningene med fingrene. Du kan da også stikke de to løse ledningene ned i vann eller holde de bort i fuktig papir eller liknende. I alle tilfellene vil lysdioden lyse. Dette viser da at vi mennesker og det meste som er fuktig vil lede strøm, om enn ganske lite strøm. Forklaringen på det som skjer er da at når vi tar på de to løse ledningene vil det gå en liten strøm gjennom B på transistoren videre gjennom oss og til pluss på batteriet. Denne lille strømmen vil i sin tur gjøre at det går en strøm som er 300 ganger større gjennom C på transistoren. Siden denne strømmen også går gjennom lysdioden vil vi da "se" denne strømmen.
Hvor stor er så den strømmen som går gjennom oss i dette tilfellet? Hvis vi antar at strømmen gjennom C og lysdioden er IC=4mA vil da strømmen gjennom B og hendene våre være
IB=4mA/300=0,013mA=13µA.
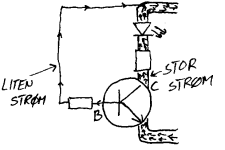
Normalt vil vi ikke merke strømmer gjennom kroppen vår som er mindre enn 0,5mA, og når vi her kan påvise at det går strøm gjennom kroppen vår så er det fordi vi har en forsterker. Transistoren forsterker altså en liten strøm ved å "lage" en annen strøm som er 300 ganger så stor og når vi sender denne strømmen gjennom en lysdioden vil denne lyse.
Noen lurer kanskje på om ikke motstanden på 1kΩ som beskytter transistoren vil redusere forsterkingen og gjøre tallene ovenfor usikre. Det vil den gjøre, men siden en typisk resistans i kroppen vår mellom to hender er på 100kΩ, så er en resistans på 1kΩ relativ liten. Tallene som brukes i dette heftet vil da alle være usikre, men hensikten med dem er da å gi talleksempler som har rett størrelsesorden. Det kan bety at tallene kanskje er feil med en faktor 2 men sannsynligvis ikke en faktor 10. Om vi i elektrisitetsammenheng aldri ser tallverdier for resistans, strøm og spenning, vil vi heller ikke oppdage den store variasjonen som finnes i disse verdiene. Et eksempel er vann. Ofte sier vi at rent vann ikke leder strøm, men forsøket ovenfor viser da helt tydelig at vann leder strøm. Det er da først når vi ser eksempler på tallverdier at vi skjønner at man kan si at 13µA er en stor strøm i noen sammenhenger men en ubetydelig strøm i andre sammenhenger.
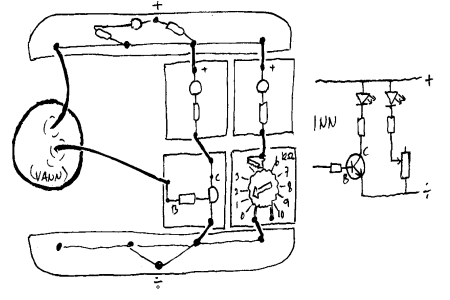
En strømmåler med stor følsomhet. Basert på prinsippet som er nevnt foran kan vi da lage en strømmåler (eller resistansmåler) tilsvarende lysmåleren vi viste i forrige kapittel. Hvis vi her antar at forsterkingen i transistoren alltid er 300 ganger kan vi lage en strømmåler som måler svært små strømverdier. Kobl til en ny lysdiode og en variabel motstand slik figuren viser:
Her vil vi da først nevne at denne strømmåleren blir upålitelig om vi kalibrerer lysmåleren som skissert her. Påliteligheten kan forbedres endel om vi kalibrerer måleren med et multimeter som viser verdier i µA-området. Poenget her er imidlertid å vise et prinsipp mer enn å lage et nøyaktig måleinstrument.

Prinsippet for strømmåleren er da den samme som lysmåleren i forrige hefte. Vi vrir på den variable motstanden til to lysdioder lyser like mye. På den variable motstanden bruker vi så en skala som viser hvor mange kΩ den er innstilt på. Videre antar vi at spenningen over den variable motstanden er fast lik 3V. (Merk at det er minimum 1,5V over en lysdiode når den lyser.) Når vi så kjenner spenning og resistans i en motstand kan vi beregne strømmen ved hjelp av Ohms lov: U=RI. U står da for spenning, R står for resistans og I står for strøm. Dette er da bare definisjonsformelen for resistans i en motstand (R=U/I), og vi vil derfor ikke bruke mer tid på den her. Her følger så et eksempel på hvordan vi går fram for å finne en verdi for strømmen som går gjennom en person som holder på de to kontaktene.
Eksempel: Vi antar da at pilen på den variable motstanden står på 1kΩ når lysdiodene lyser like mye. Vi finner så først strømmen gjennom motstanden som da er lik strømmen gjennom lysdiodene som igjen er lik kollektrorstrømmen:
Kollektorstrøm: IC = U/R = 3V/1000Ω = 3mA
Så bruker vi forsterkingen på 300 ganger og finner basisstrømmen:
Basisstrøm: IB = IC/300 = 3mA/300 = 10µA
Kretsen som er vist ovenfor (uten ekstra lysdiode og variabel motstand) kan brukes som varsler eller alarm i mange ulike sammenhenger. Om vi erstatter lysdioden med en summer vil vi få lyd i stedet for lys. I eksemplet her har vi parallellkoblet en summer og en lysdiode og praksis viser da at summeren trenger mer strøm enn lysdioden for å reagere. Rent vann og fuktige fingrer vil f.eks. lede så mye strøm gjennom B at strømmen gjennom C vil bli stor nok til å starte summeren.
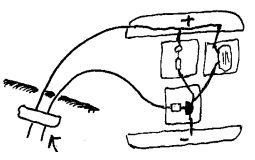
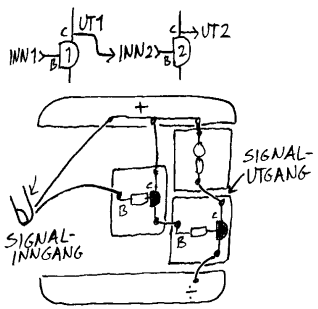
Væskenivåvarsler Om vi f.eks. vil ha et varsel når vannet i badekaret når en viss høyde kan vi da henge to stifter i den aktuelle høyden slik som vist under.
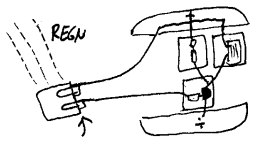
Fuktighetsalarm Om vi derimot vil ha en fuktighetsalarm/regnvarsler kan vi feste ledningene til to binderser som så i sin tur festes til en papirbit. Papirbiten kan så plasseres under åpen himmel ved hjelp av ei lenger ledning. Summeren vil da varsle når det blir regn. Merk at det går litt tid i regnevær før papiret blir så vått at summeren starter. Om du ønsker å få varsel ved de første regndråpene bør du øke forsterkingen som vist seinere i heftet.
Økt strømforsterking ved hjelp av flere transistorer
Noen mener kanskje at 300 er en stor forsterking. I elektronikksammenheng har man ofte mye høyere forsterkninger, og her vil vi da vise hvordan transistorer kan kobles sammen slik at forsterkingen blir større. Elektronikkpuslespillet inneholder to transistorer og om vi kobler disse etter hverandre vil den totale strømforsterkingen bli 300*300 = 90 000 i prinsippet. I praksis er det ulike forhold som gjør at strømforsterkningen vil variere endel i slike tilfeller, men for enkelhets skyld vil vi anta at forsterkingen virkelig blir så høy som antydet her.
Nå finnes det ulike måter å koble sammen transistorer. Prinsippet er imidlertid at signalet som går gjennom C på den første transistoren sendes inn på B på den neste transistoren. Det signalet som da kommer ut på C på den siste transistoren vil da være styrt av det signalet som gikk inn på den første transistoren. Se prinsippskissen.
Figuren viser da en mulig kobling hvor vi har en forsterkning i to trinn. Når du skal forstå virkemåten er det viktig å være klar over at signal og strøm er to ulike ting og de kan derfor ha ulik retning. Strømmen av elektroner vil alltid gå fra minus til pluss. Når vi her snakker om signal tenker vi her på variasjoner i strømstyrke. I praksis kan vi foreløpig tenke på signal som strøm eller ikke strøm. Om vi ikke berører de to ledningene som representerer inngangen på forsterkeren som er vist ovenfor vi det da ikke gå strøm gjennom lysdioden som vi da kaller utgangen. Signalet er med andre ord 0 eller ingen strøm. Om du så berører inngangen med fingrene vil du se at lysdioden blinker eller lyser. Signalet kan vi da kalle 1 eller strøm. Merk at du bør ha litt dempet lys for å kunne se når lysdioden lyser svakt.
En forklaring på virkemåten: Når det går en svært liten strøm gjennom B på den første transistoren vil denne sørge for at det kan gå en større strøm gjennom C på den samme transistoren. Denne siste strømmen vil da samtidig gå gjennom B på transistor nr 2 og C på denne transistoren vil da slippe gjennom en stor strøm. En liten strøm på inngangen medføre altså en stor strøm på utgangen.
Om vi kobler sammen to transistorer som vist her vil alarmene og varslerne som er skissert foran få en brå overgang mellom strøm og ikke-strøm og det er vanligvis en fordel når det er snakk om alarm eller varsler. Her vil vi da bare oppfordre den enkelte til å eksperimenter med ulike tilkoblinger til kretsen som er vist her. Det er liten fare for å ødelegge noe om man kun kobler ting til stiftene.
Påvisning av statisk elektrisitet og elektriske felt
Før vi forlater den enkle strømforsterkeren med to forsterkertrinn som er vist ovenfor, så vil vi bare nevne at vi her har en forsterker som har så stor forsterkning at den kan påvise både statisk elektrisitet og elektromagnetiske felt. Dette er da miljøpåvirkninger som vi ikke kan oppdage direkte ved hjelp av sansene våre, men som noen mener kan ha en uheldig innvirkning på helsen vår.
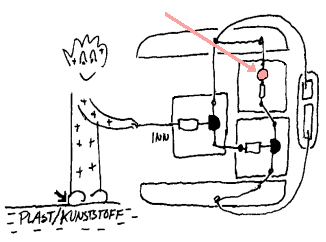
Merk først at om du berører begge ledningene på inngangen av forsterkeren, så vil lysdioden lyse. Det kommer da av at huden leder strøm og det har vi da snakket om tidligere. Men vi kan også oppleve at lysdioden lyser om vi bare berører den lederen som er koblet til basis på den første transistoren. Dette krever da en forklaring.
De fleste har vel opplevd å få elektrisk støt når man ta på metaller etter at man har vært i kontakt med kunstfiber eller liknende. Mange har vel også opplevd at håret "reiser seg" seg når man bruker kam. Dette er da forårsaket av statisk elektrisitet. Den omtalte forsterkeren kan da påvise statisk elektrisitet som da er mindre enn den som gir slike utslag som nevnt her. Hvis du tar på inngangen vil man ofte se et blink i lysdioden. Styrken og lengden kan variere, men før eller siden vil lysdioden slukne og om du så berøre den igjen uten at du har gjort noe annet, vil den vanligvis ikke blinke. Men om du f.eks. gnir fotene mot gulvet eller gjør andre ting mellom hver gang du berører ledningen vil den blinke. Det klareste beviset for at det her er snakk om statisk elektrisitet får vi vel om vi gnir fotene mot gulvet mens vi holder på lederen. Merk at det ikke er alle gulvbelegg og fottøy som gir rett positiv spenning, så det kan hende du må gjøre flere forsøk for å observere det som er beskrevet her. Tenk gjerne ut ulike forsøk for å finn ut mer om det elektrostatiske feltet i ulike sammenhenger.
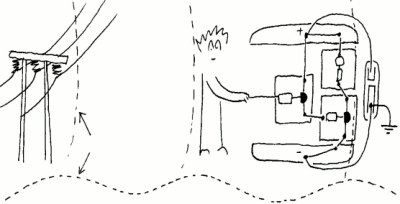
Når det gjelder elektromagnetisk stråling så er hovedkilden til denne de elektriske ledningene i og omkring husene våre. Disse fører da vekselstrøm med en frekvens på 50 Hz og den sender da ut elektromagnetiske bølger med samme frekvens. Når frekvensen er så lav betyr det at både vi og forsterkeren vil påvirkes i samme takt siden vi er små i forhold til bølgelengden (når det elektromagnetiske feltet trekker elektronene i forsterkeren i en retning, så vil også elektronene i oss som befinner oss i nærheten trekkes i samme retning). Derfor oppstår det normalt ikke noen elektrisk strøm mellom oss og forsterkeren som følge av det elektriske feltet. Men om vi jorder bare forsterkeren (kobler en ledning fra minus på forsterkeren til jord i et elektrisk støpsel eller til godset/metallet på noe som er jordet), så vil forsterkeren "ligge i ro" og ikke "svinge" med de elektromagnetiske feltene. Vi vil imidlertid fortsatt "svinge" og om vi da tar på den ene lederen på inngangen til forsterkeren vil det se ut som om lysdioden lyser konstant. Det gjør den da ikke, men fordi den blinker med en frekvens på 50Hz vil vi ikke se blinkingen. Vi fungerer med andre ord som en slags antenne som da overfører elektromagnetiske svingninger fra det elektromagnetiske feltet som omgir oss til inngangen på forsterkeren. Styrken på lyset sier da noe om hvor sterkt elektromagnetisk felt vi befinner oss i. Er du langt fra elektriske ledninger vil du kanskje ikke se lys i dioden i det hele tatt.

Her vil vi først gjenta at en transistor er en strømforsterker. Nå er det imidlertid et mål å forsterke svake signal på en nøyaktig og sikker måte med minst mulig energiforbruk. Generelt er det da slik at hvis vi øke motstandene, så vil strømmen avta. For å måle/påvise svake signal må motstanden være høy for at ikke det vi måler skal påvirkes for mye av strømmene i måleutstyret. Før eller siden blir da strømmen så liten og usikker at den er vanskelig å bruke strøm som "signalbærer". I det forrige heftet nevnte vi imidlertid at det er en sammenheng mellom høy motstand og høy spenning i seriekoblede kretser, og i det følgende vil vi derfor gå over til å bruke spenning som kjennetegn på signal i stedet for strøm. Nå er det en nær sammenheng mellom strøm og spenning og generelt vil vi ikke kunne ha det ene uten at vi også har det andre. Her velger vi imidlertid å konsentrere oss om spenningen i stedet for strømmen, og grunnen er da at det da blir lettere å forstå virkemåtene til vanlige elektroniske kretser. Transistorer og dioder har da alle en såkalt terskelspenning som innebærer at de kun virker når spenningen overstiger en bestemt minimumsverdi. Hvis vi da lar spenningen variere omkring den aktuelle terskelspenningen vil vi da kunne oppnå stor forsterkning og stor nøyaktighet i utstyret uten at det går mye strøm. Figuren til høyre kan oppfattes som to ansikt eller en vase avhengig av om vi konsentrerer oss om svarte eller hvite felt. Den andre figuren kan bli oppfattet som en gammel eller ung dame. Strøm og spenning har en tilsvarende avhengighetsforhold av hverandre. Her påstår vi da at det er lettest å forstå elektroniske kretser om vi konsentrerer oss om spenningen.
Spenningen er som tidligere nevnt den kraften som drar/skyver på elektronene, og i en transistor må vi på B (mellom B og E) ha en spenning på minimum ca 0,5V for at transistoren skal virke.
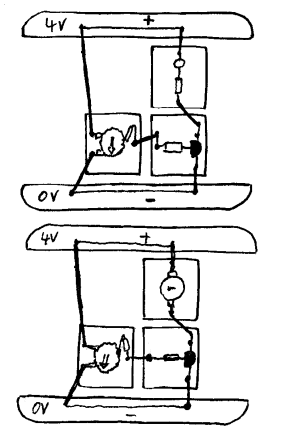
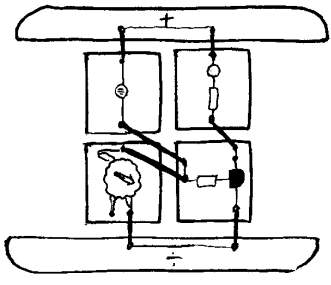
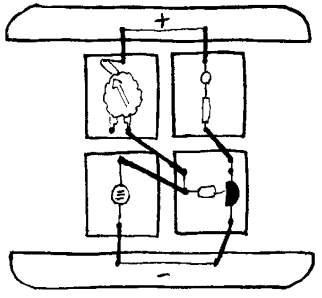
Hva skjer når vi endrer spenningen på B
Kobl opp kretsen som er vist til venstre og se hva som skjer når vi vrir på potensiometeret. Når potensiometeret kobles til 0V og 4V vil den tredje variable kontakten på potensiometeret få en spenning mellom disse ytterpunktene. Når spenningen på den tredje kontakten blir omkring 0,5V vil lysdioden slukne eller tennes avhengig av hvilke veg vi vrir hjulet. Hvis vi erstatter lysdioden med ei lyspære ser vi tydeligere at vi kan justere lysstyrken trinnløst fra fullt lys til ingen lys. Dette kalles da lysdimming. Som tidligere nevnt bør vi ikke bruke sterkere pære enn 6V/50mA i dette tilfellet fordi transistoren vi bruker ikke er beregnet på store strømmer. Men om vi erstatter transistoren med en såkalt effekttransistor vil vi da kunne koble til pærer som trekker mer strøm. Som nevnt tidligere er det fortsatt en liten strøm som styrer en større strøm.

Her velger vi imidlertid å konsentrere oss om spenningen på inngangen (B) og utgangen (C). Vi ser altså at når spenningen på B øker vil lyset øke. Grunnen til at lyset øker er da at spenningen over pæra øker fordi transistoren trekker spenningen på C ned mot 0V eller jord. Denne alternative forklaringen kan virke forvirrende i starten, men her vil vi anbefale leseren å bruke litt tid på å "koble om" fra å tenke strøm til å tenke spenning. Alle eksemplene i dette heftet kan forklares med "strømforklaringen", men de som ønsker å gå videre og forstå nye kretser og selv kunne lage enkle nyttige kretser, må lære seg å "tenke spenning". Her følger så den samme kretsen som er vist ovenfor gjengitt som tankemodell. I modellen er det da en sammenheng mellom høyde og spenning.
Lag en lysvarsler/lysstyrt alarm
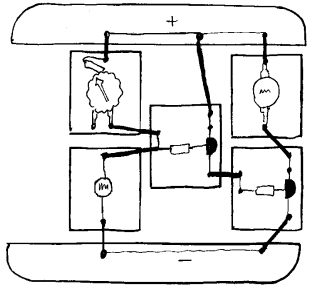
Kobl opp kretsen som er vist her. Vri på potensiometeret slik at lysdioden slukner. Vri så litt tilbake slik at dioden akkurat tenner igjen. Som figuren viser er det en motstand mellom B og 0V (potensiometer) og en motstand mellom B og 4V (lysfølsom motstand). Som nevnt i forrige kapittel er det størrelsesforholdet mellom resistansene i de to motstandene som bestemmer spenningen på B. Siden spenningen på B må være minimum 0,5V for at transistoren skal lede, vet vi da at spenningen nå er rett over denne terskelspenningen. Hvis vi så skygger for den lysfølsomme motstanden vil resistansen i denne øke, og lysdioden vil da slukne. Årsaken er da at endringen i resistansen medfører at spenningen til B kommer under terskelspenningen og dermed vil transistoren slutte å lede. Vi har dermed laget en varsler eller alarm som varsler når lysmengden øker over en viss grense som vi da på forhånd kan bestemme ved å vri på potensiometeret.
Skyggevarsler Om vi bytter plassering av potensiometeret og lysfølsom motstand, slik figuren ovenfor viser, får vi en varsler eller alarm som reagerer når det blir skygge. Den lysfølsomme motstanden vil da forårsake høyere spenning på B om resistansen øker.
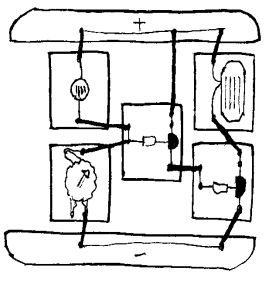
Automatisk lystenning
For å spare energi vil gatelys tennes automatisk når det blir mørkt og slukke når det blir lyst. Ved hjelp av elektronikkpuslespillet kan vi vise prinsippet for en slik automatisk lysstyring. I prinsippet kan vi da bruke koblingen fra skyggevarsleren som er vist foran og så erstatte lysdioden med lyspæra. Dette fungerer da ikke så bra fordi lyspæra trenger mer strøm enn det denne koblingen normalt vil levere. En forsterkning på 300 ganger er altså for lite. I praksis vil det være et såkalt relé som styrer strømmen til gatelys. Et relé er da en mekanisk bryter som styres av en liten strøm. I vårt tilfelle trenger vi altså mer strøm gjennom pæra og vi kan da øke forsterkningen ved å bruke to transistorer som vist til
høyre.
Vekkerklokke
Tenk deg at du ønsker ei vekkerklokke som varsler når det blir lyst, noe som da varierer med skydekke og årstid. Denne kan da se ut som vist til høyre. Denne vil da varsle når det blir lyst
Nå er det slik at lyset kommer gradvis om morgenen og variabelt skydekke kan gjøre at lysmengden både øker og minker i korte perioder. Vekkerklokka som er vist her vil derfor bruke relativt lang tid fra den får litt strøm til får så mye strøm at den gir full lyd. Selv om vi bruker to transistorer og har ei relativt stor forsterkning vil det altså være en tid hvor vi ikke vet om bryteren er på eller av. Det finnes relativt enkle elektroniske kretser som gir en rask omkobling og dessuten unngår gjentatte inn- og utkobling som følge av små variasjoner i innsignalet (eks schmittriggeren). I dette heftet vil vi imidlertid konsentrere oss om de grunnleggende prinsippene og et slikt prinsipp er da at vi kan bruke transistoren som en bryter. Men om signalene som kommer inn har svært små variasjoner, vil bryteren kunne komme i en slags mellomstilling hvor den ikke vet om den er avslått eller påslått. I mange situasjoner er det uheldig. Elektronikkpuslespillet er da laget med henblikk på at slike udefinerte tilstander ikke skal skape store problem. En datamaskin inneholder da tusenvis av transistorer og om den skal fungere rett er det nødvendig å unngå at transistorene havner i en udefinert mellomstilling.
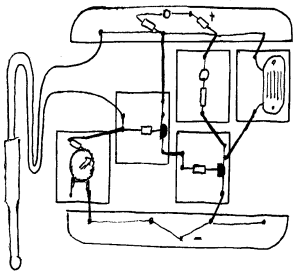
Temperaturvarsler/termostat
I elektronikkpuslespillet finnes også en temperaturfølsom motstand. Her vil vi da bare kort gi et eksempel på bruk av denne. Generelt er det da slik at en LDR (lysfølsom motstand) vil ha en mye større variasjon i resistans en NTC (temperaturfølsom motstand) under normale forhold. Det betyr med andre ord at det er vanskeligere å lage en varsler som reagerer raskt når temperaturen endres langsomt. Kobl opp kretsen som er vist her og bruk gjerne ledningsparet på 3m slik at temperaturføleren kan plasseres et stykke fra resten. Hvis du så stille potensiometeret slik at det nesten er lys/lyd kan du så bruke fingrene på den temperaturfølsomme motstanden og oppleve at summeren starter som følge av denne lille oppvarmingen. Den aktuelle kretsen kan da brukes for å varsle når temperatur i luft, vann eller annet når et visst nivå. Men som nevnt tidligere vil det være en viss udefinert mellomtilstand som gjør at temperaturene blir unøyaktige.
Som en oppsummering vil vi her da si at transistorer kan kobles sammen og få en slags bryterfunksjon. En bryter er da noe som har to stillinger, en 'på' og en 'av'. Problemet med transistorbrytere er da at en udefinert mellomstilling, men generelt er det da slik at jo flere transistorer vi bruker, jo mindre problemer får vi med denne mellomstillingen. Så langt har vi koblet lysdiode, lyspære og summer til utgangen av transistorforsterkeren. I senere hefter vil vi vise hvordan vi kan koble utgangen til en datamaskin og det åpner da for helt nye muligheter når det gjelder å behandle og lagre data som vi får fra utstyret vårt.
Til nå har vi sett hvordan motstander kan fordele spenning mellom seg og hvordan transistorer kan forsterke signal. I elektronikkpuslespillet finnes det også en kondensatorbrikke og her vil vi da vise hva kondensatorer kan gjøre i elektroniske koblinger.
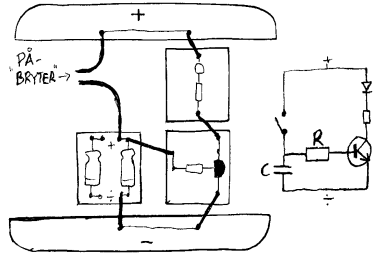
Tidsbryter
Kobl opp koblingen som er vist til venstre. Når på-bryteren kobles fra ser vi at lysdioden lyser en kort tid før den slukner. Forklaringen på denne tregheten er da at kondensatoren ble oppladet mens bryteren var på, og kondensatoren vil da levere strøm til B etter at bryteren er frakoblet. En kondensator er i praksis som et lite batteri som kan lades opp og lades ut. Den enkle kretsen som vi har her hvor en kondensator (C) lades ut over en motstand (R) er en grunnleggende krets innenfor elektronikken og den kalles da en RC-krets. Slike kretser vil da forårsake en tidsforsinkelse eller en treghet som er nyttig i mange sammenhenger. I tilhørende teorihefte vil vi gå nærmere inn på virkemåten til kondensatoren. Her vil vi da bare nevne en praktisk huskeregel for hva som kjennetegner en kondensator.
En kondensator kan lagre energi (strøm/spenning) og representerer derfor en treghet som hindrer raske forandringer |
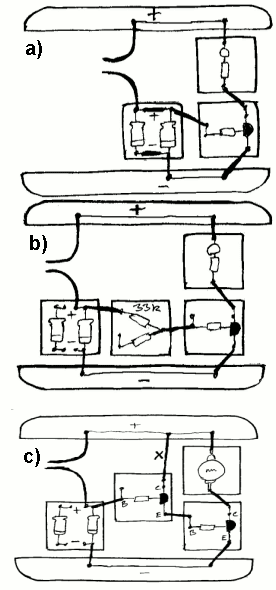
I prinsippet er det tre måter å forlenge utladingstiden til kondensatoren. Den ene er å velge en C med større kapasitans. I vårt tilfelle kan vi parallellkoble de to kondensatorene slik som vist i figur a) og lysdioden vil da lyse lenger fordi kapasitansen blir dobbelt så stor. Alternativet er å øke resistansen til R. Det kan vi da gjøre om vi kobler en resistans på 33kΩ i serie med den som er på 1kΩ. Dette er gjort i figur b) og den totale resistansen blir da 34kΩ.
En dypere forståelse for transistorens virkemåte Strømmen som lader ut kondensatoren(e) i tilfellet ovenfor vil også gå gjennom transistoren fra E til B. Her vil vi først understreke at det ikke er noen vanlig resistans her. Når først spenningen på B overstiger 0,5V vil strømmen gå tilnærmet fritt som gjennom en diode og vi antar derfor at resistansen er 0O her. Hensikten med basismotstanden på 1kO er da nettopp å hindre at vi får for stor strøm mellom E og B, da en slik stor strøm vil ødelegge transistoren.
Så langt er det ikke noe nytt i forhold til det som er nevnt tidligere. Det er først når vi kobler til en ekstra transistor som vist i c) at vi får en effekt som kanskje overrasker noen. I dette tilfellet har vi erstattet lysdioden med en lyspære som bruker forholdsvis mye strøm, og selv da får vi en ganske lang lysetid fra vi kobler fra bryteren til lyspæra slukner. Hvordan forklarer vi så dette? Nå vil det være en spenning omkring 0,5V mellom E og B på begge transistorene og det betyr da at kondensatoren vil levere strøm mens spenningen på kondensatoren faller fra 4V til ca 1V. Kravet om at det må være minst 0,5V mellom E og B på transistorene gjør altså at transistorene vil slutte å lede når spenningen over kondensatoren når 1V. Den lange lysetiden forteller da at strømmen fra transistoren er svært liten siden det går så lang tid, og det er da litt overraskende når denne strømmen bare passerer to motstander med en total resistans på 2kΩ. Hva er det så som reduserer strømmen, når det ikke er en stor resistans. Hvis vi kobler ut ledningen som er merket med X på figuren, ser vi at utladingen går så fort som vi skulle forventet med en resistans på 2kΩ. En mulig forklaring på dette "mysteriet" er da at det ikke bare er B-strømmen som styrer C-strømmen i en transistor, men C-strømmen vil også "undertrykke" B-strømmen slik at den maksimalt blir en trehundredel av C-strømmen.
Om du ikke forstår alt som er nevnt her, så er hovedpoenget at vi ovenfor har vist en krets som kan brukes for å lage relativt lange tidsforsinkelser. I utlandet er det f.eks. vanlig at lys i korridorer og på toalett styres av en tilsvarende krets. Vi trykker da bare på bryteren og lyset vil da lyse ett minutt eller mer før det så slukkes automatisk.