

2003 Erling Skaar
Finne dag og tid ved hjelp av solur
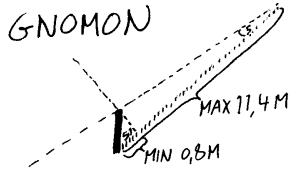
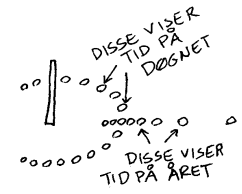
Den eldste og enkleste formen for solur er en såkalt gnomon som i praksis er en stokk eller liknende som stikker loddrett opp fra bakken. Når sola skinner vil så stokken lage en skygge på den horisontale plassen omkring og her vil det da finnes informasjon om hva klokken er når skyggen faller på den ulike stedene. Slike klokker var vanlige på offentlige steder over hele verden og statuen av Olav Tryggvason i sentrum av torget i Trondheim er da et eksempel på et slikt solur. En gromon viser da tiden på døgnet i den tiden hvor solen er oppe, men den kan også lett utvides til å vise dato eller tid på året. Vi vet at lengden på skygger varierer med årstida og om vi velger ut den lengste skyggen fra en gnomon som inntreffer ca kl 12 (ca kl 1 ved sommertid), så kan vi langs denne skyggen lage en kalender.
Hva slags krav må vi stille til selve stokken? Her vil vi da først gi noen tips til hvordan elever kan være med å utvikle "klokkedelen" og så vil vi komme tilbake til hvordan vi kan tilføye "kalenderdelen", men vi bør i utgangspunktet plassere stokken slik at den takler både klokkedelen og kalenderdelen best mulig. De færreste vil vel ha problemer med å fremskaffe og plassere en vertikal stokk som f.eks. rager 1 meter over bakken i nærheten av skolen. Problemet er imidlertid at det ikke er likegyldig hvor vi plasserer den og elevene kan da være med å vurdere plassering i forhold til solforhold og krav til en hensiktsmessig horisontal flate på skyggesiden. Mange steder i Norge vil sola være borte i store deler av vinteren, men om man i utgangspunktet har funnet en flate hvor sola også skinner om vinteren, så er det nyttig å vite at solhøyden ved vintersolverv vil være ca 5° i Volda (62° N). Dette tallet fremkommer som differansen mellom vinkelavstanden til polpunktet (90° -62° =28° ) som fortelle om solhøyden ved vårjevndøgn og høstjevndøgn og solas største vinkel sør for ekvator (ca 23° ). Det betyr videre at en 1m høy gnomon vil kaste en skygge på 11,4 meter på en horisontal flate (1m/11,4m=tg(5° )) ved vintersolverv i Volda. Hvis man da ønsker at stokken også skal fungere som en kalender hele vinteren, så må man altså ha en slette på ca 12 meter nord for stokken (eller en vegg som vi kan tegne på). Det er også verd å merke seg at sola kan være over horisonten fra kl. 3 om morgenen til 21 om kvelden på våre breddegrader og det betyr da at det i tilfelle bør være plass for en skygge i sørvestlig og sørøstlig retning hvis horisonten er lav i nordlig retning. De færreste stedene i Norge har en lav horisont helt rundt og det viktigste er da at horisonten er rimelig lav i sørlig retning der hvor sola befinner seg i skoletiden. Hvis en gnomon er for tynn vil den ikke lage en klar skygge og om den blir for tykk blir det avlesingen av tiden mer usikker. Prøving og feiling eller beregninger utfra soldiameteren på ½° kan være nyttige aktiviteter for elever.
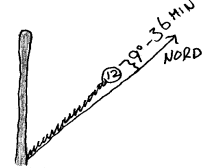
En gnomon som viser tid på døgnet Når så stokken er på plass, er neste oppgave å lage en skala. Om grunnen er asfalt kan man bruke kritt/maling eller slå ned spiker med store hoder. Om grunnen er grus eller gress, kan man bruke stein bordbiter eller liknende og i noen tilfeller er det mulig å feste slike ting ved å slå ned en kile som markøren så festes i. Poenget er at vi trenger noen faste markører omkring stokken som står fast. Når så skyggen faller på eller peker mot de ulike klokkemarkørene så skal det være lett å finne ut hva klokka er. For å unngå misforståelser om hvordan avlesingen skal skje foreslår vi her å bruke midtpunktet av skyggen og midtpunktet av markøren - ikke kanten av skyggen som kanskje kan være fristende i noen tilfeller. Når det gjelder avstanden mellom stokken og markørene så er det viktig å være klar over at skyggelengden i Volda midt på dagen ved sommersolverv fra en 1 meter høy stokk vil være ca 81 cm. Høyeste solvinkel ved sommersolverv i Volda er (90° -62° )+23° =51° (tg(51° )=81cm/100cm). Det betyr at vi bør plassere ihvertfall noen klokkemarkører ca 1 m fra stokken. Når sola er på det høyeste vil da ikke skyggen nå fram til en markør som befinner seg 1 m fra stokken, men skyggen vil da peke mot denne markøren. Når sola er lavere vil skyggen være lengere og det er ikke noe i vegen for at man også plasserer markører lenger unna for at avlesningen skal bli mer nøyaktig. Når vi så skal plassere ut markørene i rett vinkel kan vi da gjøre ett av to. Enten velger vi en soldag og møter hver time ved soluret og plasserer rett markør det skyggen er på dette aktuelle tidspunktet. Dette er en relativt tidkrevende aktivitet og vanskelig å planlegge siden sannsynligheten for at det skal være sol en bestemt dag i Norge er relativt liten. Det andre alternativet er å bruke et kompass og finne retningen mot nord. Volda har lengdegrad 6° V. Det er da de som bor på 15° V (15° =360° /24) som har sola i sør nøyaktig klokka 12 middeleuropeisk tid. I Volda vil da sola være i sør 0,6 timer = 36 min etter klokka 12 (0,6=((15-6)/15). Siden sola forflytter seg 15° på en time vil den da forflytte seg 9° på 36 min. Dette betyr altså at 12 markøren må plasseres 9° vest for nord om soluret skal gå rett. Mange synes denne matematikken er forvirrende og et alternativ er da å plassere en markør utfra en virkelig solskygge og så kan man plassere de andre markørene rett i forhold til den første markøren.
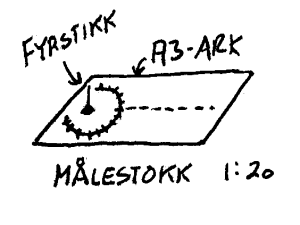
En liten modell av soluret Når man skal bygge hus er det vanlig å lage en tegning på papir først. Om vi skal lage et solur er det tilsvarende nyttig å lage en modell på papir først. Hvis vi bruker et A3 ark og en fyrstikk med høyde 5cm. Målestokken blir da 5cm:100cm=1:20. Lag så en sirkel med radius 5cm inntil kanten av en kortside. Vi tenker oss så at fyrstikken skal plasseres i sentrum av denne sirkelen. Plasser så 12 tallet som da markerer skyggen midt på dagen slik at denne skyggen peker normalt mot den kortsiden som er lengst unna. Se figur. Del så sirkelen inn i 24 (sola bruker 24 timer helt rundt) og sett klokkeslett fra f.eks. 5 til 19 ved hjelp av merker langs en sirkelbue. Vi har da en modell av et solur og vi kan da teste det ved å plassere modellen på et horisontalt underlag og vrir det slik at starttida blir rett. Da vil også alle de andre målte tidene bli rett og vi trenger altså ikke kompass.

Solkalenderen Som nevnt ovenfor kan en gnomon også brukes som en kalender og her vil vi kort skissere hva vi må tilføye til soluret ovenfor for at vi også skal kunne lese av tid på året. I prinsippet er det mulig å lese av kalendertiden ulike tider i løpet av en dag, men her vil vi forutsette at man kun leser av kalendertiden når solen er på sitt høyeste. Merk at solhøyden endrer seg lite fra 12 til 12.36 og derfor blir feilen ikke merkbar om vi antar at sola har sin største vinkelavstand fra horisonten klokken 12. I et virkelig solur kan man da male en rett linje på asfalten eller legge ned et eller flere bord gjennom 12-markeringen. I modellen tegner vi da en tallinje fra fyrstikken gjennom 12-punket og det er da langs denne linjen at vi markerer ulike datoer. Skyggelengden vil da peke på noen datoer og utfra dette kan vi lese av en cirka dato.
Hvordan vet vi så hvor vi skal plassere de ulike datoene. I Almanakk for Norge finnes en tabell som viser "Solsenterets deklinasjon (vinkelavstand fra himmelekvator) og solhøyde over horisonten ved middagstid. Denne er noenlunde lik fra år til år og nedenfor har vi plukket ut noen ca. verdier, to fra hver måned:
Datoer: |
|
Dekl: |
Polv: |
Solh: |
Skygge[m] |
|
|
21.12 |
-23 |
28 |
5 |
11,4 |
6.1 |
6.12 |
-22 |
28 |
6 |
9,5 |
21.1 |
21.11 |
-20 |
28 |
8 |
7,1 |
6.2 |
6.11 |
-16 |
28 |
12 |
4,7 |
21.2 |
21.10 |
-11 |
28 |
17 |
3,3 |
6.3 |
6.10 |
-6 |
28 |
22 |
2,5 |
|
21.3 |
21.9 |
0 |
28 |
28 |
1,88 |
|
6.4 |
6.9 |
6 |
28 |
34 |
1,48 |
|
21.4 |
21.8 |
11 |
28 |
39 |
1,23 |
|
6.5 |
6.8 |
16 |
28 |
44 |
1,04 |
|
21.5 |
21.7 |
20 |
28 |
48 |
0,90 |
|
6.6 |
6.7 |
22 |
28 |
50 |
40,8 |
|
21.6 |
|
23 |
28 |
51 |
0,81 |
Polvinkel til Volda (vinkelen mellom oss og nordpolen) er da 28°
og om vi summerer Deklinasjon og polvinkel får vi solhøyda oppgitt i grader. Hvis vi så bruker tangens (tg) på en kalkulator kan vi finne lengden til en skygge som en 1m lang vertikal stokk lager: skyggelengde=1/tg(v). Hvis vi så skal finne skyggelengden i modellen vår som har målestokk 1:20 så kan det være nyttig med litt hoderegning og man kan da halvere tallene ovenfor og så flytte kommaet ett hakk slik som antydet her: 1,48 -> 0,74 -> 0,074 (=7,4cm)
Den ferdige modellen viser da at skyggen blir uhensiktsmessig lang om vinteren og det kan derfor være en fordel å ha en vegg 2-3 meter nord for stokken. Man kan da markere vinterdatoene på denne veggen og det blir da lettere å lese av siden skyggen er skarpere jo nærmerer man befinner seg. Problemet er kanskje å beregne hvor merkene skal plasseres. Et tips i denne sammenhengen er å bruke en stor tavletranspotør og et vater og så kan en markere punktene mens noen andre sikter inn.
Vise lokale solmerker ved hjelp av OH
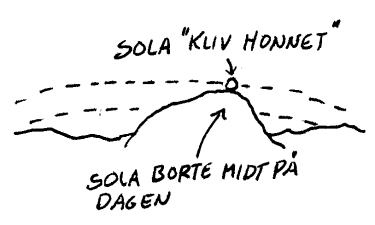
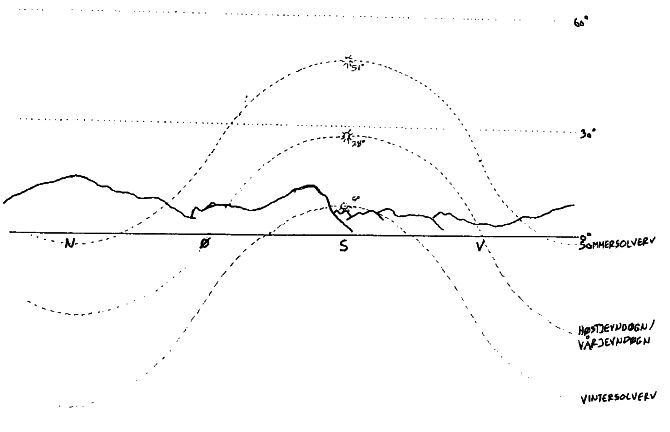
Tidligere generasjoner var flinkere til å observere det som skjer på himmelen enn dagens generasjoner. Kanskje er tiden inne til å lære de nye generasjonene noen grunnleggende observasjonsteknikker? I Volda er snakker man f.eks. om datoen når sola dukker fram for første gang om våren, når sola "kliver honnet" (det vil si at den går over Rotsetthornet) og hvor sola går ned ved Jonsok. Det er altså snakk om å observere hvor sola befinner seg i forhold til den lokale horisonten til ulike tider. Vi kan så klippe en sol av gul plast og så plassere den ulike steder i forhold til horisonten som befinner seg på veggen. Vi kan da videre sette på klokkeslett som vertikale linjer som skjærer horisonten bestemte steder og disse kan da være til hjelp om vi vil anslå tida utfra solas stilling. Når det gjelder solhøyden vil den variere i løpet av året, og det er også mulig å tegne inn de ulike banene som den følger. I denne sammenhengen er det nyttig å vite at solbanen blir ensinuskurve hvor amplituden er lik polavstanden (28°
for Volda). Skissen under viser hvordan sola beveger seg i forhold til horisonten sett fra Kårstadbygget i Volda.

Hjemmelaget
solhøydemåler
I ulike sammenhenger kan det være aktuelt å måle solhøyden. Solhøyden er vinkelen mellom horisontalplanet og solstrålene som når oss. Om sola er svært lavt eller dekkes av halvgjennomtrengelige skyer er det mulig å se på sola, men generelt må vi aldri legge opp til aktiviteter hvor elevene skal se på sola. Hvordan er det da mulig å måle solhøyden. En måte er å lage en solhøydemåler slik som vist på figuren til høyre. Gravitasjonskraften har retning 90°
på horisontalplanet og det er da den som stiller inn skiva slik at skyggen fra sola viser rett vinkel. Solhøydemåleren kan da lages av vanlig hvit kartong og vinklene kan da tegnes over på pappen fra en tavletransportør. I sentrum plasserer man så en liten stift/spiker og det er da denne som lager skyggen som viser solhøyden. Man kan da bruke denne for å måle solhøyden flere ganger i løpet av en dag og da vil man kunne på et tid-høyde-diagram få fram en sinuskurve. En annen variasjon er å erstatte gradene med datoer slik som vist i forbindelse med solkalenderen. Hvis man da henger solhøydemåleren i nærheten av et sørvendt vinduet kan man bruke den som en kalender som viser en ca. dato.
Nå er det relativt få detaljer vi kan se med bare øynene i universet. Vi kan f.eks. se et mønster på månen, men vi må ha kikkert for klart å se at det er snakk om fjell og sletter med en mørkere farge. En kikkert på f.eks. 7x50 er grei å bruke om vi ønsker å se nærmere på nattehimmelen. Med en slik kikkert er det da også mulig å se Jupiters måner og endel flere stjerner enn de vi ser med bare øynene. Men generelt er det lite ekstra å se om vi bruker kikkert og når man er ute med barn om kvelder så der det vel mest aktuelt å konsentrere seg om noen kjente stjernebilder og eventuelt si navnet på planeter om disse er synlige.
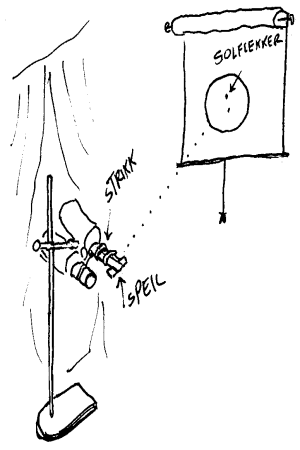
På dagtid er det vanligvis bare sola som er synlig, men månen og noen planeter kan også være synlig. Nå vet vel alle at man ikke må se direkte på sola og det er da en selvfølge at man heller ikke må kikke inn i en kikkert som rettes mot sola. Her vil vi imidlertid kort vise en måte som man kan observere sola og se solflekker uten fare for øynene. En kikkert er laget for å gi stor forstørring av fjerne gjenstander og til høyre vises et enkelt oppsett hvor vi fester en vanlig 8X40 eller 7X50 prismekikkert i et stativ og fester et speil til kikkerten. NB: Kikk aldri direkten mot sola gjennom en kikkert! Når så kikkerten rettes mot sola vil den lage an avbildning av sola som speilet reflektere opp i taket eller på en annen hvit flate. Merk at det er mulig å få solbildet skarpt ved hjelp av den vanlige skarpstillingen til kikkerten. Ved hjelp av dette oppsettet er det da mulig å se solflekkene på sola og det er da også mulig å se at sola beveger seg, siden bildet forflytter seg relativt fort. Solskiva vil f.eks. forflytte seg sin egen diameter i løpet av 2 minutt (x/(24*60)min=0,5° /360° ). Det skjer også på himmelen men her er det verre å observere det fordi vi aldri må se direkte på sola. De andre himmellegemene sender da ut så lite lys at det er mer hensiktsmessig å se på disse direkte gjennom kikkerten i stedet for å lage avbildninger på hvite flater.
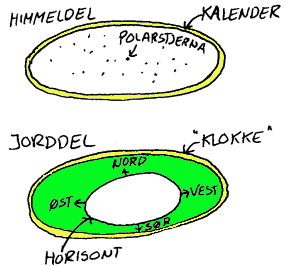
Finne stjerner ved hjelp av en stjernefinner
En stjernefinner består av en "himmel-del" som er et stjernekart hvor en forholdsvis stor del av stjernehimmelen er projisert inn på et flatt ark. På samme måten som det oppstår forvrengning når ei rund jord skal inn i på flate ark i en atlas, så vil det også være forvrengninger i et stjernekart. I tillegg til en fast "himmel-delen" (stjernekartet) så består stjernefinneren også av en vridbar "jord-del" som da er ment å være horisonten til observatøren. På horisonten er det da markert hvor vi finner nord, sør, øst og vest. Jorddelen er i praksis et sirkelformet hull og alt inni sirkelen er da den delen av stjernehimmelen som vi til enhver tid ser. Det er da verd å merke seg at halve himmelen vil befinne seg inni sirkelen til en hver tid selv om det ikke ser slik ut på det flate stjernekartet. I ytterkant av stjernekartet er det da avsatt en "kalender" (datoer og måneder) og en hel runde svarer da til ett år. Denne omliggende kalenderen viser da retningen til sola i forhold til polarstjerna i løpet av året. Sett fra jorda ser det altså ut som sola beveger seg i en sirkel på himmelen (
ekliptikken - gul sirkel på stjernekartet nedenfor) og denne sirkelen går da gjennom de 12 stjernebildene i dyrekretsen (Zodiak). Polarstjerna befinner seg i midtpunktet av stjernekartet. På "jord-delen" av stjernefinneren er det da en "klokke" som går til 24.
stjernefinner for utskrift til skriver
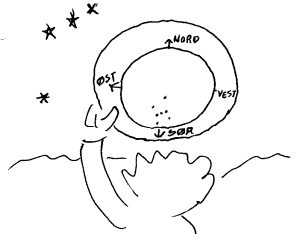
Bruken av stjernefinneren er enkel. Det forutsettes at man kjenner dato og klokkeslett for når observasjonen skal foregå. Man vrir så "kalenderen" i forhold til "klokken" slik at rett klokketid og rett dato står overfor hverandre. Da vil stjernefinneren vise hvordan stjernehimmelen ser ut på det tidspunktet, inkludert hva som er nord, øst, vest og sør. I motsetning til et vanlig kart som vi skal "se ned på", må vi her holde stjernekartet over oss for at nord, øst, vest og sør skal komme rett i forhold til hverandre. Nå er det tungvint å stå å se rett opp med stjernefinneren over hodet, og tanken er da at man velger å se i en retning (nord, øst, vest eller sør) og så holder vi stjernefinneren foran oss slik at pilen for den aktuelle himmelretningen peker ned. Stjernekartets nederste halvdel vil da gi et bilde av den delen av himmelen som vi da ser. Det krever da litt øving i å kjenne igjen de ulike stjernebildene. På stjernekartet finne man da bare et utvalg av de sterkeste stjernene og hjelpestrekene som ofte finnes på stjernekart finnes da ikke på himmelen.
For barna i småskolen er jorda ufattelig stor og det er vel begrenset hva de kan oppfatte når det gjelder størrelsene i universet. L97 nevner imidlertid at man skal arbeide med en "modell" for solsystemet og her vil vi da bare kort skissere hvordan man kan lage en skalamodell som viser rett størrelsforhold mellom jorda, sola og månen. I tabeller kan vi f.eks finne følgende data:
|
|
Diameter |
Avstand fra jorda |
|
Jorda |
13 000 km |
|
|
Månen |
3 500 km |
380 000 km |
|
Sola |
1 400 000 km |
150 000 000 km |
En enkel metode for å lage en skalamodell er da å f.eks. tegne ei sol på tavla som er har diameter 1,4m (1mm svarer til 1 000 km) og så klippe ut jorda og månen i samme målestokk fra et ark. De tre figurene vil da vise innbyrdes størrelsforhold og i neste omgang er det så mulig å plassere dem i en avstand fra hverandre slik at også avstanden blir i samme målestokk. Mange blir overrasket når de ser hvor lita jorda er i forhold til avstandene og størrelsene til våre nære naboer i universet. Nå er de aktuelle avstandene basert på visse antakelser som ikke er 100% sikre og det kan tenkes at man i framtiden må revidere de oppgitte verdiene.
Skalamodell av solsystemet:
Tabellen viser et annet forslag til størrelse og avstand i en
modell av solsystemet. Merk at 30 m mellom sola og jorda betyr
at man sannsynligvis ikke får plassert begge disse i et klasserom. Når
13 millioner meter blir 2,6 mm (13 000 000 000 -> 2,6) blir målestokken
1:500 000 000
|
jord |
13->2,6mm |
|
|
måne |
3,5->0,7mm |
380->7,6cm |
|
sol |
1400->28cm |
150 000->30m |
Skalamodell av avstander i universet
Om vi velger å lage en modell hvor sola er 0,7mm blir målestokken
1:200 000 000 000 og vi får da følgende avstand og størrelse:
|
|
avstand fra sola |
diameteren til himmellegemene |
|
a-centauri: |
21km |
0,7mm |
|
Sirius: |
44km |
3mm |
|
Polarstjerna: |
3 300km |
6mm |
|
Betelguse: |
2 600 km |
50cm |
Disse verdiene overrasker de fleste og det er da mulig at avstander og størrelser i universet kanskje må revideres i framtida.

Modell som forklarer hvorfor vi ser ulike stjernebilder ved ulike årstider
Figuren viser hvordan man kan plassere noen
utvalgte stjernebilder. Personen som går
rundt sola med jorda i hånden må gå 'mot klokka' og dreie jorda '
mot klokka'. Merk videre at jordaksen alltid må helle samme retning (mot
skytten)
Noen vinkeleksempler
I astronomien er vi oftest interessert i å finne vinkelen mellom to siktlinjer. Vi befinner oss da i skjæringspunktet mellom siktlinjene. Her vil vi kort nevne noen tips om hvordan vi kan anslå vinkler uten å bruke avanserte instrument. Følgende er ofte et godt utgangspunkt for å anslå størrelser på ulike
synsvinkler:
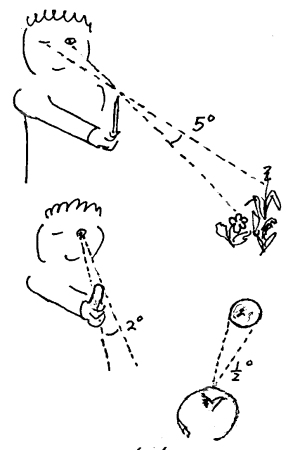
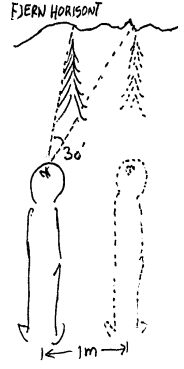
1 Holder vi en blyant eller liknende på strak arm. Når vi blunker vekselvis med hvert øye vil blyantens tilsynelatende forflytning mot bakgrunnen tilsvare ca 5°.
2 Holder vi hånda rett fram med løftet tommel vil tommelens brede tilsvare ca 2° .
3 Diameteren til sola og månen tilsvarer en vinkel på ca 1/2° .
I astronomien er vi ofte interessert i vinkler som er mindre enn en grad. En grad er delt opp i 60 bueminutter (') og hvert bueminutt er igjen delt opp i 60 buesekunder ("). Vi får et inntrykk av hvor stort et bueminutt er om vi tegner 1 mm tykke streker 1 mm fra hverandre på et ark. Hvis vi så plasserer dette arket 2,7 m unna, vil hver strek tilsvare 1'.
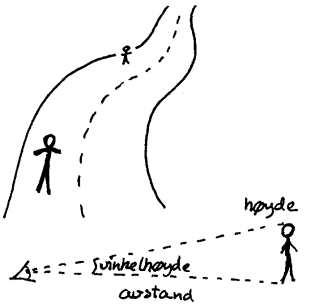

Beregning av størrelser ved hjelp av vinkler
Vinkler er en viktig faktor når det gjelder å beregne størrelse og avstand til objekt. Ofte vil vi ubevisst anslå størrelse og avstand til ulike gjenstander uten at vi tenker over at det er vinkler som ligger bak. Om vi ser to personer et stykke fra hverandre på en veg, vil den nærmeste ha en større vinkelhøyde. Men siden den andre befinner seg lenger unna vil vi automatisk justere for dette om vi skal anslå hvilken person som er størst. Nå er det mye som kan forstyrre vår innebygde beregning av størrelse og avstander. Derfor kan det av og til være nyttig å gå litt mer vitenskapelig til verks. Generelt vil vi ha 3 variable faktorer: vinkel, avstand og størrelse. Kjenner vi to av dem, kan vi beregne den tredje.
Boermetoden kan bare brukes på jorda
En enkel metode for å beregne avstand, kalles boermetoden. Denne baserer seg på at vinkelen mellom øynene og en blyant el.l. holdt på strak arm, er ca. 5°
for alle mennesker. Videre forutsetter den at vi kjenner størrelsen på en eller annen gjenstand som befinner seg ved objektet som vi skal beregne avstanden til. Det kan f.eks. være et menneske (2m) en bil (5m) et hus (10m) eller liknende. Ved å holde en blyant eller liknende på strak arm og blunke annenhver gang med øynene, kan vi så utfra kjente størrelser beregne hvor langt blyanten flytter seg. Det tallet vi får
her skal så multipliseres med 10 og resultatet blir avstanden.

Parallaksemetoder kan brukes i universet
Om vi ikke vet noe om størrelsen til objektet som vi ønsker å finne avstanden til, kan ovennevnte metode ikke brukes. I utgangspunktet kjenner vi hverken størrelse eller avstanden til himmellegemene. Vi kjenner bare avstander her på jorda og prinsippet i paralaksemetoden er da at vi tar
utgangspunkt i en kjent lokal avstand. Vi forflytter oss så mellom endepunktene til den lokale avstanden og måler så vinkelen til et fjernt legeme. Til høyre har vi vist denne situasjonen. Vi kan da forflytte oss langs grunnlinjen i trekanten og måle denne med f.eks. metermål. Når vi befinner oss i endepunktene i trekanten kan vi da måle vinkelen mellom grunnlinjen og et fjernt punkt og i den aktuelle trekanten vil
vi da kjenne grunnlinjen og to vinkler. Vi kan da bruke kjente matematiske formler for å beregne den
tredje vinkelen de to andre sidene i trekanten
Alle som har kjørt bil eller tog har observert at nære gjenstander synes å forflytte seg mer enn fjerne gjenstander. Horisonten og svært fjerne gjenstander synes nesten ikke å bevege seg i det hele tatt. Dette prinsippet kan utnyttes til å beregne avstanden til ulike nære objekt. Denne metoden forutsetter altså at vi har en fjern horisont med tilnærmet uendelig avstand som referanse for vinkelmålinger. I parallaksemetoden er da prinsippet at observatøren forflytter seg en kjent avstand. Det objektet vi ønsker å beregne avstanden til, vil da forflytte seg litt i forhold til bakgrunnen. Vinkelen til denne forflytningen kan relativt lett måles. Om den fjerne bakgrunnen ikke ligger rett bak objektet, kan vi bruke en loddsnor som hjelpemiddel for å måle denne forflytningen. Når vi så kjenner en avstand og har funnet en vinkel, kan vi beregne avstanden til den aktuelle gjenstanden. Til slike beregninger trenger vi et relativt nøyaktig vinkelmål. Om vi plasserer en linjal i enden av et sammenrullet A4-ark som da er ca 30 cm langt, og kikker gjennom rullen på linjalen, vil hver millimeter tilsvare ca 10'. Denne vinkelmåleren kan vi så bruke til å anslå vinkelforflytningen, og avstanden kan da utledes utfra tabellen nedenfor. Metoden kan brukes på trær og bygninger i nærheten av skolen. Merk at bakgrunnen som vi beregner forflytningen i forhold til, må være mye lenger unna enn objektet vi beregner avstanden til. Følgende tabell kan brukes for å omgjøre vinkler til avstander.
Målt vinke:l |
1m forflytning: |
5m forflytning: |
10m forflytning: |
1° |
57m |
280m |
570m |
30' |
110m |
550m |
1,1km |
10' |
340m |
1700m |
3,4km |
5' |
690m |
3400m |
6,9km |
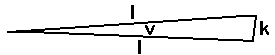

Når vi bruker vinkler for å beregne avstander, har vi vanligvis en trekanter med to lange sider (l) og en kort side (k) og vinkelen mellom de to lange sidene (v). Formelen: sin(v)=tg(v)=k/l gjelder tilnærmet for trekanter hvor det er snakk om en kort side og to lange sider som er mye lenger enn den korte.
1 Bruk ovennevnte formel for å finne ut hvor langt fra hverandre to streker må tegnes på tavla for at personen med
en avstand på 3 m skal se en vinkel mellom dem på:
a) 2°
k=______ b) ½°
k=______
Øyevinkel(blunke med utstrakt hånd): 5°
Tommelbreddevinkel(utrakt hånd): 2°
Sol/måne-diameter: 0,5°
=30'
Øyets oppløsning: 0,008°
=0,5'=30" (gjennomsnittsperson)
b) Egen øyevinkel:_____
Egen tommelbredde:________
c) Plasserer ark med strekfelt med 1mm streker i avstand 3 m. Hva blir synsvinkelen til hver enkel strek/mellomrom i avstand 3 meter? _______
Finn øyets oppløsning til en personer ved å be han
plassere seg i en avstand hvor strekfeltet går over til å bli en
grå flate. l:______ k:________ Øyets oppløsning v:______________
Kommentar:
a) 2°
på 3 meter blir 10cm (tommelbredde) 5°
på 3 meter blir 26cm (øyevinkel)
c) 1mm i avstand 3 meter svarer til 1,1' (bueminutt)
Om strekene er synlig på 6 m har vi: sin(v)=1mm/6m => Maksimal oppløsning: v=0,6'=34" (buesekund)

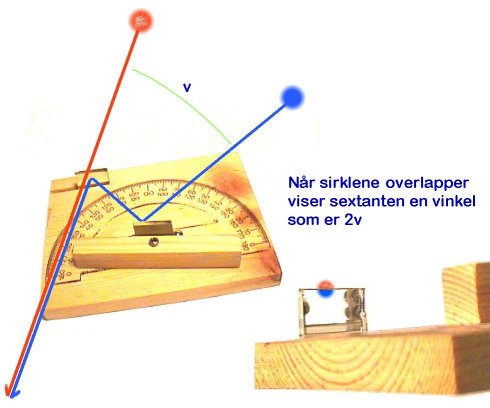
Bildene viser profesjonell sextant og hjemmelaget sextant:

Hjemmelaget sextant Siden vinkelskalaen på denne er hentet fra en vanlig transportør må man dobble avlest vinkel for å finne virkelig vinkel. Når man bruker kunstig horisont skal man ved bruk av vanlig sextant halvere den vinkelen man får, noe man slipper når man bruker den hjemmelagede sextanten. Merk at den hjemmelagede sextanten bare har en oppløsning omkring ½ grad mens en profesjonell sextant har en oppløsning ned til ca 1 bueminutt. Bruk ikke hjemmelaget sextant til å måle solhøyde da denne mangler filter til å demper sollyset.

1 Vinkelhøydemåling .
Fremgangsmåte: Bruk hjemmelaget sextant og ei skål som er full med vann
eller et horisontalt speil (kalles kunstig horisont). Plasser deg så slik at du ser det du skal måle vinkelhøyden til både i vannflata og direkte. Bruk så sextanten til å føre de to delene sammen. Når så de to toppene berører hverandre vil sextanten vise vinkelhøyden
direkte. (Om man bruker en vanlig sekstant må man halvere verdien når
man bruker kunstig horisont).
a)Bruk dette prinsippet til å bestemme vinkelhøyden (v) til Rotsetthornet. v=________
Kommentar
Hjemmelaget sextant gav 14,5°
og siden vinkelen fra denne må halveres samtidig som bruk av kunstig horisont innebærer en dobling av vinkel, så er vinkelhøyden til Rotsetthornet 14,5°
Til venstre vises prinsippet for den hjemmelagede sextanten. Hvis man vrir hendelen til 0°, så vil vi over og i speilet se den røde kulen (om alt er rett justert og man kikker rett). Når vi så skal finne vinkelen mellom den røde og blå kula vrir vi så på hendelen slik at den blå kula vises i speilet der den røde kula var (se figur) og da vil sextanten vise en vinkel som er dobbelt så stor som den virkelige vinkelen mellom kulene. Merk at vinkelen blir unøyaktig om kulene er for nær den som måler. En sextant fungerer best når vi måler vinkler mellom gjenstander som er langt borte.
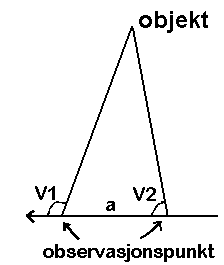
2 Avstandsmåling v.h.a. lokal avstand og to lokale vinkler
Fremgangsmåte: Mål først vinkel mellom objekt og en linje som er ca 90°
i forhold til målelinja (v1). Bruk et fjernt punkt som endepunkt for den tenkte linjen. Forflytt deg så kjent avstand (a) på f.eks. 1 m og gjør en ny vinkelmåling (v2). Avstanden til objektet blir: l=a/tg(v) når v=|v1-v2|.
Bruk dette prinsippet sammen med hjemmelaget sextant og finn avstanden til flaggstanga.eller
nærmeste hus
Avstanden til:________ v1=____ a=_____ v2=____ l=_____
Hva er den maksimale avstanden man kan måle med denne metoden om man antar at sextanten har en oppløsning på 1° og man kan forflytte seg maksimalt 5 meter _____
Kommentar:
Målte vinkel mellom flaggstanga og et punkt ca 90°
unna, før og etter at vi hadde forflyttet oss 1 meter normalt på siktelinja til flaggstanga. Forskjellen i vinkel vi målte i disse to tilfellene var 84°
-80°
=4°
. Formelen sin(4°
)=1m/l gir flaggstangavstand: l=14m
Hvis oppløsningen til hjemmelaget sekstant er ½°
vil maksimalavstanden vi kan måle ved å forflytte oss 5m være i størrelsorden l=5m/sin(0,5)=570m
3 Parallaksemetoden( lokal avstand og "fjern vinkel")


Linjalvinkelmåler: Om man ønsker å måle små vinkler ned til ca 5 bueminutt (5') kan man holde en linjal i en avstand på ca 69 cm (strak hånd) og da vil hver mm på linjalen svare til ca 5 bueminutt mens 12 mm svarer til en grad.
Fremgangsmåte: Forutsetningen for at denne metoden skal gi rett verdi er at man ser en horisont som er mye fjernere enn det vi skal måle avstanden til (målepunktet). Om horisonten er langt over målepunktet kan en loddsnor være til hjelp. Merk først et punkt på horisonten som står rett bak/over objektet. Forflytte deg så en kjent avstand (a) sidelengs og merk deg et nytt punkt på horisonten som ligger rett bak/over objektet. Mål så hvor stor vinkel målepunktet har forflyttet seg i forhold til horisonten (v).
Bruk dette prinsippet sammen med linjalvinkelmåler og bestem avstanden (l) til et
tre i nærheten og en bygning nede i sentrum.
Tre: a=_____ v=__________ l=a/sin(v)=_______
Bygning: a=_____ v=__________ l=a/sin(v)=_______
Kommentar:
Bildene ovenfor av en tretopp er tatt gjennom 2 vinduer
med avstand 1m mellom. Skalaen som er lagt på bildene øverst viser
grader (5 bueminutt er ca 1 mm i linjalvinkelmåleren) og vi får
avstand:
l=1m/sin(1)=57m
Parallaksemetoden brukt på pipe i Volda sentrum med Folkestadfjellene som referanse gav en vinkelforflytning på 10' når vi forflyttet oss 4,5m. Formelen sin(10')=4,5m/l gir: l=1,5km