 Erling Skaar (17.1.01)
Erling Skaar (17.1.01)^2000 EM1 EM2 EM3 EM4 Aktiviteter Oppgaver 00UV 01UV 02UV 03UV 04UV 05UV
Elektrisitet og magnetisme 3:
Elektrisk strøm
 Erling Skaar (17.1.01)
Erling Skaar (17.1.01)
Innhold:
Innledning om strøm
Elektrodynamikken er den delen av elektrisitetslæren hvor elektrisk strøm er en vesentlig del. I elektrostatikken var det da snakk om relativt mye spenning og lite strøm, mens her er det da snakk om relativt små spenninger, men mye strøm.
 Litt historikk
Litt historikk
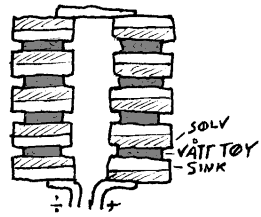
Grunnlaget for elektrisk strøm var kjent før 1800, og man hadde også laget maskiner som kunne produsere store statiske spenninger ved at stoff ble gnidd mot hverandre. Men denne elektrisiteten hadde liten praktiske verdi. Det var først da man klarte å produsere en viss mengde elektrisk strøm at utviklingen skjøt fart. Her vil vi først nevne en oppdagelse som på en spesiell måte inspirerte datidens forskere til å studere det vi i dag kaller elektrisk strøm. I 1786 observerte Luigi Galvani (1737-1798) at metalltråder som ble stukket inn i en froskefot kunne aktivisere musklene. Han mente at han hadde oppdaget en slags "dyre-elektrisitet". Disse forsøkene var en medvirkende årsak til at Alsessandro Volta (1745-1827) i 1800 laget det første batteriet. Dette bestod av alternerende lag av sinkskiver, sølvskiver og stoff som var dynket i en saltløsing. Han hadde da oppdaget at det oppstod små spenninger når ulike metaller ble stukket ned i saltløsinger og ved å koblet sammen flere celler kunne han få så mye strøm at den kunne brukes til noe praktisk. Ved hjelp av slike batteri ble det da gjort mange ulike forsøk i tiden som fulgte. Batteriet er fortsatt en viktig strømkilde, men det var da først etter at Michael Faraday (1791-1867) oppdaget induksjonen som igjen var grunnlaget for å produsere strøm ved hjelp av dynamo/generator at man fikk så mye strøm at folk flest kunne gjøre seg nytte av denne.
 Et interessant trekk ved vitenskapens oppdagelse av elektrisitetens hemmelighet er at de ulike grunnleggende oppdagelsene ikke førte til en umiddelbar anvendelse av kunnskapen. Et problem var at det kreves kreativitet for å kunne "se" hva elektrisiteten kan brukes til i en tid hvor elektrisiteten ikke ble brukt til noe nyttig. Et annet problem var at det tok relativ lang til fra elektrisiteten ble oppdaget, inntil man klarte å fremskaffe større mengder med stabil strøm. I de siste hundre årene kan vi vel si at det er brukt svært store ressurser på å produsere mest mulig stabil elektrisk energi på en billigst mulig måte. I dag har vi derfor rikelig tilgang på elektrisk strøm, selv om vi aldri kan si at vi har fått nok. Et kjennetegn på vår tid er da en kontinuerlig søking etter å finne nye anvendelser for elektrisk strøm. Hovedmotivet bak den elektriske tannbørsten er vel ikke en etterspørsel eller et utbredt behov, men muligheten for å tjene penger på et nytt produkt.
Et interessant trekk ved vitenskapens oppdagelse av elektrisitetens hemmelighet er at de ulike grunnleggende oppdagelsene ikke førte til en umiddelbar anvendelse av kunnskapen. Et problem var at det kreves kreativitet for å kunne "se" hva elektrisiteten kan brukes til i en tid hvor elektrisiteten ikke ble brukt til noe nyttig. Et annet problem var at det tok relativ lang til fra elektrisiteten ble oppdaget, inntil man klarte å fremskaffe større mengder med stabil strøm. I de siste hundre årene kan vi vel si at det er brukt svært store ressurser på å produsere mest mulig stabil elektrisk energi på en billigst mulig måte. I dag har vi derfor rikelig tilgang på elektrisk strøm, selv om vi aldri kan si at vi har fått nok. Et kjennetegn på vår tid er da en kontinuerlig søking etter å finne nye anvendelser for elektrisk strøm. Hovedmotivet bak den elektriske tannbørsten er vel ikke en etterspørsel eller et utbredt behov, men muligheten for å tjene penger på et nytt produkt.
Elektrisk strøm i dag
Det som er nevnt tidligere om elektrisitet og magnetisme er relativt fjernt fra folk flest. Hovedgrunnen er vel at elektrisk utstyr fungere selv om vi ikke skjønner hvordan de fungerer. Når det derimot gjelder begrepet elektrisk strøm, så er dette et begrep som de fleste opplever som relevant i hverdagen. De fleste har vel opplevet at det er mye som stopper opp om strømmen forsvinner. Dette betyr vel at folk flest er mer motivert for å lære noe om strøm enn mye av det andre som er omtalt i dette heftet. Elektrisk strøm er et praktisk begrep som brukes i mange sammenhenger, men det betyr ikke nødvendigvis at det er enkelt å forstå. Hensikten med dette kapitlet er da å gi en grunnleggende forståelse for hva som ligger i begrepet elektrisk strøm.
 I Norge får vi hoveddelen av vår elektriske strøm fra vannkraft. Det betyr at det er potensiell energi i vann som omdannes til elektrisk energi. Her er det verd å merke seg at strømmen produseres i samme øyeblikk som vi forbruker den i lyspærer og alt det andre vi omgir oss med. Strømmen dannes i generatorer som bygger på induksjonsprinsippet som Faraday oppdaget, og føres til oss via et elektrisk kraftnett som da er strømførende ledninger. Vi bruker da denne strømmen til oppvarming, lys og mye annet.
I Norge får vi hoveddelen av vår elektriske strøm fra vannkraft. Det betyr at det er potensiell energi i vann som omdannes til elektrisk energi. Her er det verd å merke seg at strømmen produseres i samme øyeblikk som vi forbruker den i lyspærer og alt det andre vi omgir oss med. Strømmen dannes i generatorer som bygger på induksjonsprinsippet som Faraday oppdaget, og føres til oss via et elektrisk kraftnett som da er strømførende ledninger. Vi bruker da denne strømmen til oppvarming, lys og mye annet.
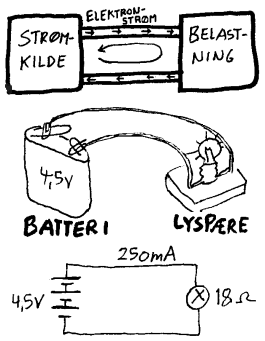
 Elektrisk strøm er "elektroner som forflytter seg" og slik sett er den enkel å forstå. Men det er da ikke selve strømmen som bør få æren for alt som blir utført elektrisk utstyr. Når strømmen er så nyttig som den er, så er det fordi man har utviklet en teknologi som utnytter elektrisk strøm som energikilde. Om vi så ønsker å forstå det som skjer i det elektriske utstyret vi omgir oss med til daglig, så er det viktig å forstå endel grunnleggende prinsipp og lovmessigheter og det er da det vi vil konsentrere oss om her. Målet med dette heftet er å hjelpe leseren til å forstå grunnprinsippene i elektrisitetsforsyningen.
Elektrisk strøm er "elektroner som forflytter seg" og slik sett er den enkel å forstå. Men det er da ikke selve strømmen som bør få æren for alt som blir utført elektrisk utstyr. Når strømmen er så nyttig som den er, så er det fordi man har utviklet en teknologi som utnytter elektrisk strøm som energikilde. Om vi så ønsker å forstå det som skjer i det elektriske utstyret vi omgir oss med til daglig, så er det viktig å forstå endel grunnleggende prinsipp og lovmessigheter og det er da det vi vil konsentrere oss om her. Målet med dette heftet er å hjelpe leseren til å forstå grunnprinsippene i elektrisitetsforsyningen.
Elektrisk strøm kan enten være vekselstrøm eller likestrøm. Forskjellen på vekselstrøm og likestrøm er da at vekselstrømmen skifter retning flere ganger i sekundet, mens likestrømmen alltid har samme retning i lederen. Her vil vi i første omgang trekke fram endel lovmessigheter og begrep som er felles for både vekselstrøm og likestrøm. Vi vil da senere komme tilbake til en nærmere forklaring av de to strømformene og se på noen praktisk eksempler. Her er det viktigst å vite at vi vanligvis får likestrøm fra batteri, mens vi får vekselstrøm gjennom lysnettet. Her vil vi ellers kort nevne at vi kan bruke både vekselstrøm og likestrøm til lyspærer og varmeovner. Når det derimot gjelder elektromotorer og det meste av det andre utstyret vi omgir oss med, så er de da konstruert enten for vekselstrøm eller likestrøm.
 Fakta om strøm
Fakta om strømI naturen vil vi ikke ha strøm uten at vi har en strømkrets. Grunnen er da at naturen motsetter seg store konsentrasjoner av ladninger, som man da ville fått om man bare flyttet elektroner fra et sted til et annet. Det betyr videre at strømkilden som driver strømmen må både avgi og ta imot elektroner for at det skal gå strøm. Grunnen til at vi nevner dette her er at dette sannsynligvis er et nyttig tankeprinsipp som kan være til hjelp når man skal forstå definisjonene som følger.
Strøm (I) er 1)elektroner (ladninger) som forflytter seg i samme retning (kvalitativ definisjon) 2)ladniningsmengde (gjennom et tverrsnitt) pr. tidsenhet: I=Q/t [A=C/s] (kvantitativ definisjon)
Strømkrets er en krets (ring) med ledende materiale som inkluderer en strømkilde.
|
 Det som er nevnt ovenfor er grunnbegrepene i den såkalte Ohms lov: V=RI som er en eksperimentell lovmessighet som gjelder tilnærmet i mange praktiske situasjoner, men den gjelder da ikke for ikke for såkalte halvledere (dioder, transistorer ol.). Fordi loven er så enkel er den nyttig når vi ønsker å finne kvantitative verdier for spenning og strøm i hele strømkretser eller i deler av strømkretser og enkeltkomponenter. Siden loven ikke gjelder i alle sammenhenger bør man derfor ikke basere forståelsen av strøm og spenning på denne. Da vil man i tilfelle få problemer med å forstå virkemåten til grunnkomponentene i moderne elektronikk.
Det som er nevnt ovenfor er grunnbegrepene i den såkalte Ohms lov: V=RI som er en eksperimentell lovmessighet som gjelder tilnærmet i mange praktiske situasjoner, men den gjelder da ikke for ikke for såkalte halvledere (dioder, transistorer ol.). Fordi loven er så enkel er den nyttig når vi ønsker å finne kvantitative verdier for spenning og strøm i hele strømkretser eller i deler av strømkretser og enkeltkomponenter. Siden loven ikke gjelder i alle sammenhenger bør man derfor ikke basere forståelsen av strøm og spenning på denne. Da vil man i tilfelle få problemer med å forstå virkemåten til grunnkomponentene i moderne elektronikk.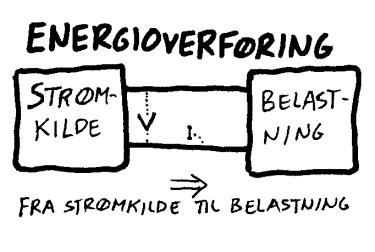
En annen viktig formel er effektformelen: P=VI som forteller oss hvor mye energi som er involvert i elektriske kretser. |
Siden P=Energi/t og I=q/t så får vi også Energi=Vq som da kan brukes som en kvantitativ definisjon av spenning.
Her følger videre en liste over sentrale begrep innenfor elektrodynamikken som vi skal komme tilbake til:
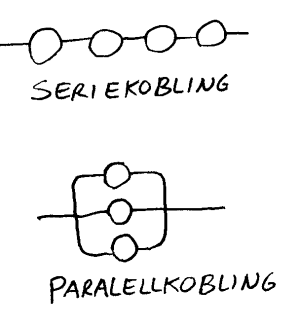
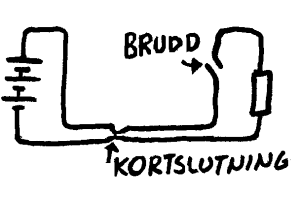
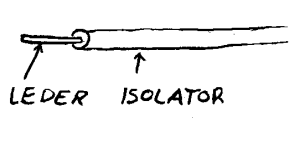
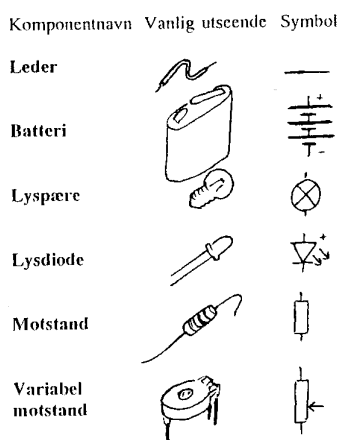
Seriekobling - når komponenter er koblet etter hverandre slik at den samme strømmen går gjennom alle komponentene. Parallellkobling - når strømmen fordeles gjennom to eller flere komponenter. Kortslutning/overledning - feilsituasjon hvor resistansen i kretsen blir for liten. Store strømmengder kan da ødelegge ting. Brudd - feilsituasjon hvor resistansen i kretsen blir for stor og strømmen blir da tilnærmet 0. Koblingskjema oversikt over elektrisk krets hvor komponenter er erstattet med symbol. Leder - har liten resistans Isolator - har stor resistans |
 Litt kvalitativt om strøm
Litt kvalitativt om strøm Før vi ser på noen konkrete strømkretser, vil vi her først prøve å danne oss et fysisk bilde av hva som ligger i begrepene strøm, resistans og spenning.
Hva er strøm?
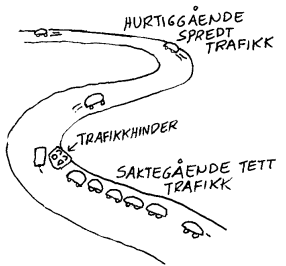
Begrepet strøm er det relativt lett å forstå fordi det er lett å danne seg et indre bilde av hva det handler om. På en vei kan vi f.eks. ha en strøm av biler. Her vil vi kort understreke at det ikke er farten til bilene eller antall biler hver for seg som bestemmer strømmen, men det er da en kombinasjon av begge disse. Bilstrømmen (antall biler som passerer et punkt pr minutt) kan f.eks. være den samme om man har en tett saktegående kø eller om vi har spredte biler med høy hastighet. Elektrisk strøm er vanligvis elektroner som beveger seg gjennom en leder, og generelt kan da mange saktegående elektroner gi like mye strøm som få raske elektroner.
 Hvorfor er spenning og resistans vanskelige begrep?
Hvorfor er spenning og resistans vanskelige begrep?
Spenning og resistans er to andre viktige begrep som da bestemmer hvor stor elektrisk strøm vi skal ha i konkrete tilfeller. Disse er da begrep som mange har problemer med å forstå. Årsaken kan være at lærebøker har mislykkes med å gi et nyttig indre bilde av hva som egentlig ligger i disse begrepene. Her vil vi bruke litt tid på å bygge opp en fysisk forståelse for hva som ligger i de aktuelle begrepene slik at man har noe konkret å tenke på når man senere skal anvende dem i konkrete situasjoner. Alternativet blir ofte en slags manipulering med diffuse begrep som før eller senere fører til at forståelsen erstattes med pugging.
Grunnlaget for å forstå spenning og resistans er at man forstår hvordan elektronene er plassert i atomene. Ifølge kvantemodellen er det snakk om en slags diffuse elektronskyer som beveger seg i baner omkring atomkjernene. Dette er en pedagogisk dårlig modell av atomet, som i mange tilfeller fungerer som et "slør" som hindrer forståelse og "dreper" interessen for fysikk. Mange mener også at det er en faglig dårlig modell som hemmer moderne forskning.
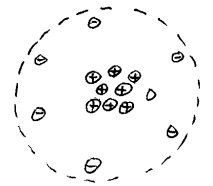 En pedagogisk atommodell
En pedagogisk atommodell
I praktiske kjemi- og fysikksammenhenger har man vanligvis valgt å betrakte elektronene som små ladninger som befinner seg i bestemte posisjoner i atomet, og dette vil vi da også gjøre her. Elektronene befinner seg da mer eller mindre nær kjernen i atomet og ifølge em-modellen er det magnetiske og elektriske krefter som holder dem på plass. Hvis vi f.eks. prøver å "puffe" et elektron nærmere kjernen vil magnetiske krefter motvirke dette. Om vi så prøver å "dra" elektronet bort fra kjernen vil elektriske krefter motvirke dette.  Tilsvarende vil omliggende elektroner også lage elektriske og magnetiske krefter som gjør at et elektron heller ikke vil kunne bevege seg rundt kjernen. Elektronene befinner seg altså i et såkalt potensialhull som da er forårsaket av elektriske og magnetiske krefter fra omgivelsene. Denne situasjonen har mange likhetstrekk med ei kule i et fat med avrundet bunn. Kula vil alltid føle en kraftsum som trekker den mot sentrum av skåla, men den kan da oscillere eller svinge litt fram og tilbake. Hvis svingningene blir for store kan så kula hoppe over kanten. Tilsvarende kan vi også tenke at elektroner kan forlate et potensialhull.
Tilsvarende vil omliggende elektroner også lage elektriske og magnetiske krefter som gjør at et elektron heller ikke vil kunne bevege seg rundt kjernen. Elektronene befinner seg altså i et såkalt potensialhull som da er forårsaket av elektriske og magnetiske krefter fra omgivelsene. Denne situasjonen har mange likhetstrekk med ei kule i et fat med avrundet bunn. Kula vil alltid føle en kraftsum som trekker den mot sentrum av skåla, men den kan da oscillere eller svinge litt fram og tilbake. Hvis svingningene blir for store kan så kula hoppe over kanten. Tilsvarende kan vi også tenke at elektroner kan forlate et potensialhull.
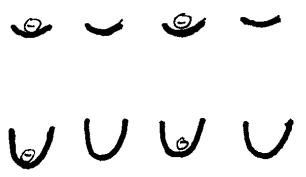 Hva er resistans?
Hva er resistans?
Tidligere har vi definert resistans som noe som hindrer strøm, og som et indre bildet kan vi tenke på resistansen som et uttrykk for hvor høye kanter det er i potensialhullet. Ulike stoff har ulike resistans. Et isolerende stoff vil da ha svært stor resistans og det betyr da at alle elektronene befinner seg i dype potensialhull. Det er da vanskelig å løsrive eller flytte på elektroner. Metaller er på den andre siden gode ledere og det betyr da at de har mange potensialhull med relativt lave kanter.
 Termisk energi gjør at elektroner beveger seg
Termisk energi gjør at elektroner beveger seg
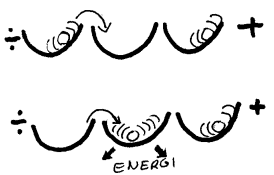
Temperatur er et utrykk for hvor mye elektronene svinger fram og tilbake i potensialhullene sine. Jo høyere temperaturen er jo mer svinger de. Elektronene vil da aldri ligge helt i ro i et potensialhull. Dette betyr videre at elektroner ofte hopper fra ett hull til et annet, men fordi denne hoppingen har tilfeldig retning snakker vi ikke om elektrisk strøm i dette tilfellet. Elektrisk strøm kjennetegnes av at mange elektroner beveger seg i samme retning. Når elektronene i et stoff vibrere sender de ut elektromagnetiske bølger som absorberes av naboelektron og slik sett vil de kontinuerlig utveksle energi som kan gi enkeltelektroner nok energi til å hoppe over i et nytt potensialhull. Et elektron som ramler ned i et nytt potensialhull vil da vibrere bort overskuddsenergien som elektromagnetiske bølger og slik kan vi tenke oss at energien overføres mellom elektronene samtidig som totalenergien er konstant.
 Hva skjer når vi kobler til et batteri?
Hva skjer når vi kobler til et batteri?
Hva skjer så hvis vi kobler en motstandstråd (leder med litt stor resistans) til et batteri? Motstandstråden vil da oppleve et overskudd av elektroner ved minuspolen og et underskudd av elektroner ved plusspolen. Mellom disse vil det da oppstå et elektrisk felt som vil forskyve elektronene i potensialhullene i motstandstråden. Elektriske krefter gjør da at elektronene vil bli trukket litt oppover kanten av potensialhullene (mot plusspolen). Det svarer da til at elektronene får hjelp til å hoppe over i et nytt potensialhull. Resultatet blir at flere elektroner enn normalt vi hoppe over til nye potensialhull og totalt sett får vi en elektronstrøm mot plusspolen. Hver gang et elektron ramler ned i et potensialhull vil det frigjør energi i form av elektromagnetiske bølger eller varmestråling, og denne strålingen vil da øke når det går strøm gjennom motstandstråden. Derfor blir motstandstråden varm.
 Hva er spenning?
Hva er spenning?
Tidligere har vi presentert formelen som viser hvor mye energi som omdannes fra elektrisk energi til varme i elektrisk utstyr: P=VI. Her vil vi da bruke denne for å danne oss et fysisk bilde av bidraget fra spenningen V. De fleste vil oppleve det innlysende at energiomformingen fra elektrisk energi til varme er proporsjonal med antall elektroner som er involvert. Her vil vi derfor konsentrere oss om det fysiske innholdet i begrepet spenning(V). I et homogent elektrisk felt (homogent felt betyr at feltet er like sterkt i hele området) har man følgende sammenheng: V=Ed (d er lengden av motstandstråden). Siden spenningen er proporsjonal med det elektriske feltet som igjen er proporsjonalt med de elektriske kreftene (E=F/q) betyr det at spenningen forteller noe om kraften som trekker elektronene ut fra sentrum i potensialhullene. Dette gjør at vi kan bruke kraft som et begrep som karakteriserer spenningen og det er dermed mulig å danne seg et fysisk bilde av spenningen gjør i motstandstråden. 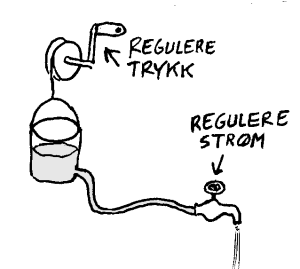 Vi tenker altså på spenning som en "kraft" som trekker elektroner ut fra sentrum i potensialhull. Ifølge formelen V=Ed så er det også en d involvert, og her vil vi bare si at det skjer en energiomforming fra strøm til varme langs hele motstandstråden og derfor må vi tenke på spenningen som en "totalkraft" og ikke en enkel kraft som virke på et enkelt elektron. I et energiperspektiv kan vi da si at den aktuelle "totalkraften" gjør at elektronene som hopper starter "høyere" i potensialhullet sitt enn de ender i det nye potensialhullet og denne energiforskjellen er da bidraget fra spenningen.
Vi tenker altså på spenning som en "kraft" som trekker elektroner ut fra sentrum i potensialhull. Ifølge formelen V=Ed så er det også en d involvert, og her vil vi bare si at det skjer en energiomforming fra strøm til varme langs hele motstandstråden og derfor må vi tenke på spenningen som en "totalkraft" og ikke en enkel kraft som virke på et enkelt elektron. I et energiperspektiv kan vi da si at den aktuelle "totalkraften" gjør at elektronene som hopper starter "høyere" i potensialhullet sitt enn de ender i det nye potensialhullet og denne energiforskjellen er da bidraget fra spenningen.
Når vi her beskriver spenningen som en "kraft" så bruker vi "" for å marker at det ikke er snakk om en kraft slik den er definert i mekanikken. Nå har det også vært brukt andre ord som 'trykk', 'energi' og 'arbeid' i forsøk på å gi en fysisk forklaring av hva som ligger i begrepet spenning. Det er selvfølgelig mulig å avvise alle slike forsøk og si at 'spenning' er 'spenning'. Dette er da selvfølgelig rett, men problemet er da at denne definisjonen av spenning gir liten hjelp til å danne oss et indre bilde av hva det dreier seg om. Erfaring har vist at vi mennesker trenger hjelpeforklaringer for å danne oss indre bilder av det vi skal forstå. Alternativet er da å pugge det "ekspertene" har sagt, men det er det vel bare ekspertene som er tjent med.
 Skoleaktiviteter
SkoleaktiviteterI skolen ønsker man vanligvis å gi en innføring i grunnprinsippene i elektrisitetslæra, og det er da et ønske om å unngå kompliserende forhold. Sammenhengen mellom elektrisitet og magnetisme er en kompliserende faktor som vi her har utsatt til neste kapittel. Her vil vi da prøve å presentere elektrisiteten som et "rent" elektrisk fenomen. Det betyr at vi kan trekke inn begrep som leder, isolator, bryter, strømbrudd, kortslutning, sikring, lyspære, varmeovn, parallellkobling, seriekobling ol, men vi styrer unna motorer, ringeklokken, elektromagneter, transformatorer ol., men vi vil ikke gi en grundig forklaring av virkemåten. Disse vil vi da komme tilbake til i neste kapittel. 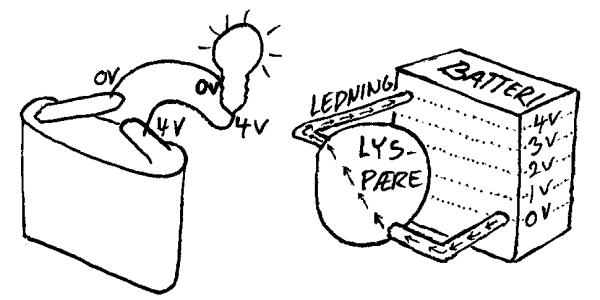 Når elevene skal lære om elektrisitet er det viktig å gjøre undervisningen konkret. Her følger da noen forslag til aktiviteter hvor et 4,5V batteri og en lysdiode utgjør kjernen. Lysdiodens hovedoppgave er da å markere når det går strøm, og den vil da lyse med langt mindre strøm enn ei lyspære. Det betyr på den ene siden at vi sparer energi og på den andre siden kan vi påvise langt svakere strømmer enn om vi brukte ei lyspære. Hensikten med motstanden diodebrikken
er da å sikre at lysdioden ikke får mer strøm enn den tåler.
Når elevene skal lære om elektrisitet er det viktig å gjøre undervisningen konkret. Her følger da noen forslag til aktiviteter hvor et 4,5V batteri og en lysdiode utgjør kjernen. Lysdiodens hovedoppgave er da å markere når det går strøm, og den vil da lyse med langt mindre strøm enn ei lyspære. Det betyr på den ene siden at vi sparer energi og på den andre siden kan vi påvise langt svakere strømmer enn om vi brukte ei lyspære. Hensikten med motstanden diodebrikken
er da å sikre at lysdioden ikke får mer strøm enn den tåler.
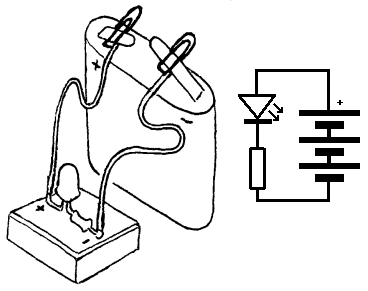 Aktivitet 1
Aktivitet 1
Kobl opp kretsen som er vist til høyre. Lysdioden skal lyse om koblingen er rett. Mulige grunner til at lysdioden ikke lyser:
- Lysdioden snudd feil vei (dioder leder strøm bare en vei)
- Defekt batteri, defekt lysdiode, ledningsbrudd
Forklaring:
Kretsen bruker relativt lite strøm (ca. 8mA). Den kan derfor være oppkoblet en stund uten at batteriet tappes noe særlig. Studer derfor kretsen mens du leser forklaringene som følger her. Når lysdioden lyser betyr det at vi har elektrisk strøm. Elektrisk strøm betyr at det går elektroner fra minuspolen på batteriet gjennom en motstand og gjennom en lysdiode til plusspolen på batteriet. Ikke tenk at enkeltelektroner beveger seg helt fra minuspolen til plusspolen på batteriet. Figuren
viser også koblingskjemaet til strømkretsen. Det er da en enkel krets hvor lysdioden lyser når det går strøm, og hensikten med motstanden på 330W er da å beskytte lysdioden mot å få for mye strøm/spenning.
 Ledere og isolatorer
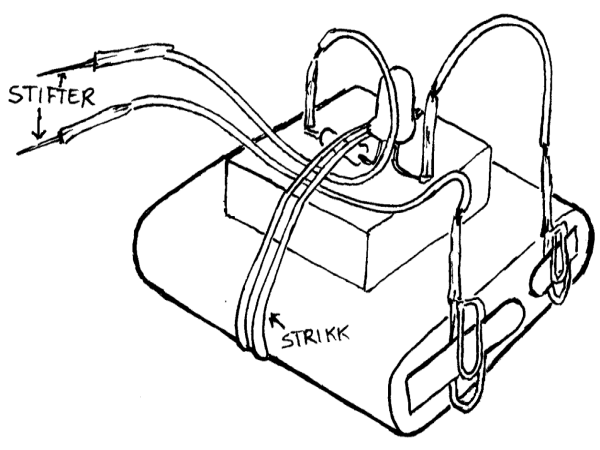
Ledere og isolatorerAktivitet 2: Lag en ledningsevnetester
Når det oppstår feil i elektrisk utstyr, skyldes dette ofte strømbrudd. Til
høyre vises en nyttig tester som kan brukes for å finne strømbrudd i tillegg til at den også kan teste ledningsevne i ulike stoff.
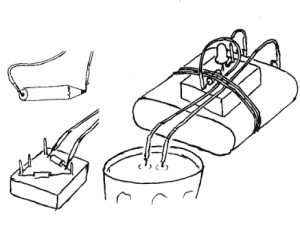 Problemstilling: Hva leder strøm?
Problemstilling: Hva leder strøm?
Et viktig kjennetegn på stoffene som omgir oss er om de leder strøm eller ikke. Hvis et stoff leder strøm kaller vi det en leder. Om det ikke leder strøm kaller vi det en isolator. Her vil vi da først bruke testeren til å sjekke hva som leder strøm. Nå er det vanlig å snakke om gode og dårlige ledere, og ved hjelp av testeren som er vist her kan vi skille mellom disse. Om lysdioden lyser mye når vi tester stoffet sier vi da at vi har en god leder. I skjemaet nedenfor kan vi markere det med stor 'L'. Om lysdioden lyser lite, sier vi da at vi har en dårlig ledere og vi skriver da en liten 'l' i skjemaet nedenfor. Om lysdioden ikke lyser sier vi da at vi har en isolator og vi skriver da bokstaven 'i' i skjemaet. Merk at det også finnes gode og dårlige isolatorer og det er da mulig å lage et instrument som kan skille mellom disse. Til venstre vises hvordan man tester motstanden på 1000W og vann.
Finne ledningsevnen i ulike stoff Ledningsevnetesteren til å sjekke de tingene/stoffene som er nevnt i tabellen nedenfor leder strøm. Føy selv til nye ting/stoff.
| Ting/stoff | L/l/i | Ting/stoff | L/l/i |
| En nøkkel | Luft | ||
| Trebit | Stein | ||
| Papir | Appelsin | ||
| Blyantbly (grafitt) | Rent vann | ||
| Plast | Saltvann | ||
| Hud/fingrer | Saft | ||
| Melk | |||
 Noen konklusjoner om ledere og isolatorer
Noen konklusjoner om ledere og isolatorer
Etter at ledningsevnen i ulike stoff er undersøkt, er det naturlig å prøve å trekke noen konklusjoner. Her vil vi da nevne noen generelle konklusjoner som eventuelt kan brukes for å kontrollere egne data. Generelt er metaller gode ledere. På den andre siden har vi plast, gummi, glass, luft ol. som regnes som gode isolatorer og de brukes derfor ofte som isolasjon rundt elektriske ledninger. Andre stoff vil da lede strøm mer eller mindre. En generell regel er da at fuktighet (tilstedeværelse av vann) gjør mange stoff ledende. Et eksempel er kjøkkensalt. Tørre saltkorn leder ikke strøm, men når det blandes ut i vann leder det strøm. Generelt kan vi si at jo fuktigere et stoff er, jo bedre leder det strøm. Til vanlig regner vi ikke rent vann som en leder men det
er lett og vise at vann heller ikke er en isolator. Her vil vi derfor kalle rent vann, hud ol. for dårlige isolatorer, men om det er mørkt omkring oss så vil vi kanskje
kunne se at lysdioden lyser når vi putter ledningsendene i rent vann.
Problemstilling 2: Søke etter feil/strømbrudd i elektrisk utstyr
Testeren som er vist foran kan også brukes til å søke etter brudd og feil i elektrisk utstyr. Her følger noen tips. 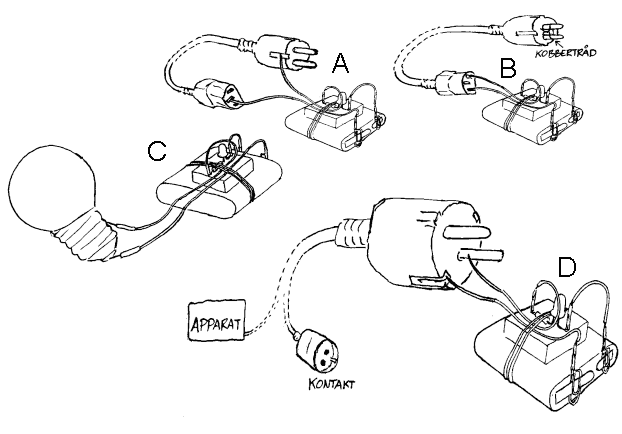 Sjekke lyspærer: Vanligvis sjekker man en lyspære (glødelampe) ved å sette dem inn en holderen og tilføre beregnet spenning (220V, 12V, oa.). Men om det er tungvint eller upraktisk så kan vi koble til testeren slik som vist til høyre og lysdioden vil da lyse om pæra er i orden
(C). Vanligvis vil glødetråden ryke når pæra går og da virker testeren. Men om det er en indre kortslutning i lyspæra vil lysdioden lyse selv om pæra er defekt, men sansynligheten for slike feil er liten.
Sjekke lyspærer: Vanligvis sjekker man en lyspære (glødelampe) ved å sette dem inn en holderen og tilføre beregnet spenning (220V, 12V, oa.). Men om det er tungvint eller upraktisk så kan vi koble til testeren slik som vist til høyre og lysdioden vil da lyse om pæra er i orden
(C). Vanligvis vil glødetråden ryke når pæra går og da virker testeren. Men om det er en indre kortslutning i lyspæra vil lysdioden lyse selv om pæra er defekt, men sansynligheten for slike feil er liten.
Påvise brudd i kabler/ledninger: Det finnes mange ulike løse kabler og skjøteledninger. Brudd i disse gjør at det elektriske utstyret som bruker kablene ikke virker eller blir farlig å bruke. A
og B vise eksempler på hvordan vi kan sjekke om det er brudd i slike ledninger. NB! Ledninger og kabler må alltid trekkes ut av kontakten før de testes. Det er livsfarlig å berøre ledninger som er tilkoblet 220V. Ledningen som er vist her har to ledere som fører strøm og en jordledning. På figur A testes jordledningen. Om det er brudd på denne kan apparatet fortsatt virke, men det kan da bli farlig å bruke det i våte rom. Prøving og feiling er ofte nødvendig for å finne hva som hører sammen når det gjelder strømledningene, hvis du da ikke er så lur at du kobler de to lederne sammen i den ene enden og kobler testeren til den andre enden (B).
Påvise jordingsfeil: Hvis det er kontakt mellom en av strømledningene og jordledningen kan det føre til farlige strømstøt hos brukeren. Nyere sikringsbokser vil koble ut strømmen ved slike feil, men det skjer ikke i eldre sikringsbokser. I
figur D vises hvordan man kan teste om det er overledning i en ledning eller i et elektrisk apparat. Om lysdioden lyser når man berører jord sammen med en av strømlederne, er det en jordingsfeil og apparatet/ledningen må ikke brukes. (Merk at lysdioden skal lyse om man berører begge strømlederne fra et apparat, hvis bryteren står på og apparatet er i orden.)
Aktivitet 3: Lag en enkel lysdimmer
Kobl opp kretsen som er vist her. Om vi vrir på den variable motstanden så vil lyset fra lysdioden endre seg.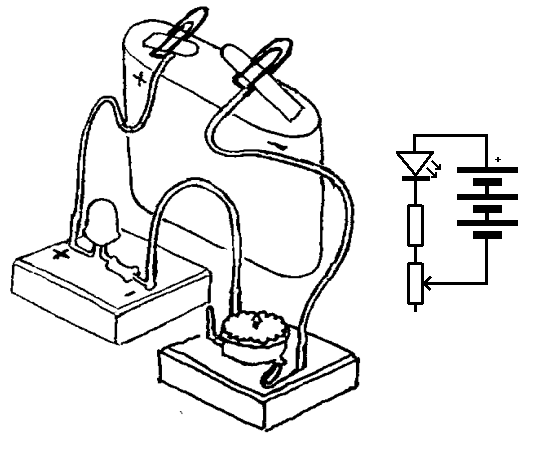
Forklaring:
Når vi skal forklarer det som skjer i elektriske strømkretser har vi tre ulike ord eller begrep som kan brukes. Disse er strøm (benevning: mA), spenning (benevning: V) og resistans (motstand) (benevning: O). Siden alle disse begrepene er avhengige av hverandre er det vanskelig å lære om ett begrep av gangen, og det er også vanskelig å si at ett begrep er mer grunnleggende enn de andre. Her vil vi imidlertid anta at resistansen (motstanden) er mest grunnleggende. Årsaken er da at vi kan endre resistansen i en strømkrets på ulike måte og denne endringen vil da medføre endring i strøm og spenning. En endring i strøm og spenning vil normalt ikke medføre endring av resistansen.
Forsøk viser da at når vi øker resistansen i en krets vil strømmen avta. En lysdiode eller ei lyspære vil lyse mer jo mer lys som går gjennom den, og derfor kan vi se når det går mye og lite strøm i denne kretsen. Når det gjelder den variable motstanden, så blir resistansen større når pila fjerner seg fra den endekontakten som brukes.
Strømbrudd
Strømbrudd er i prinsippet det samme som om vi setter inn en motstand som har for stor resistans i kretsen. Grunnen til at pæra til høyre ikke lyser er for stor motstand(A) og brudd(B) (men batteriet tappes ulikt mye) 
Kortslutning
En kortslutning er egentlig en strømkrets med for liten resistans. I praksis er det ingen som ønsker å lage slike strømkretser, men det kan da oppstå feil som gjør at strømmen tar snarveier som ikke var meningen. Generelt er det slik at elektronstrømmen velger "minste motstands vei" fra minuspolen til plusspolen. Det er da vår oppgave å passe på at det ikke oppstår snarveier utenom komponentene. Hensikten med motstandene er f.eks. å redusere strømmengden til et passende nivå. Men hvis elektronene "ser" at det finnes snarveier til plusspolen utenom "de anviste rutene" så startes det et "stormløp" som kan få uheldige konsekvenser. Eksempler på kortslutninger er vist til venstre: I tilfelle A går strømmen direkte mellom bindersene i stedet for å gå gjennom lyspæra. I tilfelle B går strømmen utenom motstanden og lysdioden vil få for mye strøm slik at den ødelegges. 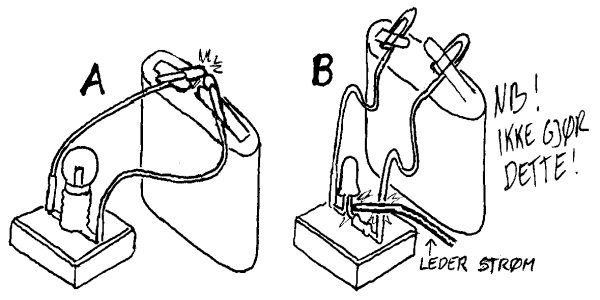
Sikring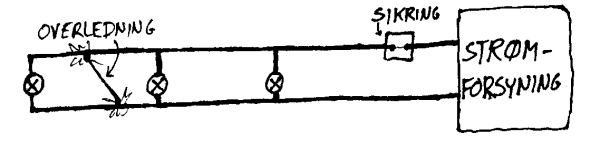 For å unngå slike skadevirkninger bruker vi sikringer i ulike sammenhenger. Ei sikring er ofte
en leder som "brenner opp" om det går mer strøm enn det den er beregnet for. Tidligere har vi lært at strømmen i en strømkrets øker når resistansen avtar. Om vi så har en strømkrets med en resistans nær 0W vil strømmen bli svært stor. En kortslutning er uheldig av flere grunner:
For å unngå slike skadevirkninger bruker vi sikringer i ulike sammenhenger. Ei sikring er ofte
en leder som "brenner opp" om det går mer strøm enn det den er beregnet for. Tidligere har vi lært at strømmen i en strømkrets øker når resistansen avtar. Om vi så har en strømkrets med en resistans nær 0W vil strømmen bli svært stor. En kortslutning er uheldig av flere grunner:
1) Batteri blir fort oppbrukt (energisløsing)
2) Komponenter blir varme og kan ødeleggesNår sikringen går, vil strømmen brytes og dette hindrer da at andre mer kostbare komponenter skal ødelegges eller at ledninger skal bli varme og starte brann. Sikringer er koblet inn i en krets for å hindrer både at ledninger og komponenter går varme og blir ødelagt. Dessuten beskytter de også strømforsyningen slik at den ikke blir overbelastet.
 Seriekobling
og paralellkobling
Seriekobling
og paralellkobling
Nå er det lettere å forklare forskjellen mellom seriekobling og parallelkobling ved å bruke figurer enn ved å bruke ord. Koblingsskjemaene viser to seriekoblede og to parallellkoblede lyspærer.
 Seriekobling av resistanser
Seriekobling av resistanser
En måte å definere en serikobling er å si at komponentene er koblet i serie når de er koblet etter hverandre slik at den samme strømmen går gjennom alle komponentene. Hvilke av firkantene til venstre er seriekoblinger utfra definisjonen ovenfor?
Parallellkobling - når strømmen deler seg
Ofte lar vi en spenningskilde (batteri) sørge for strøm til mange ulike komponenter. I prinsippet finnes det to måter å koble komponenter til en spenningskilde. 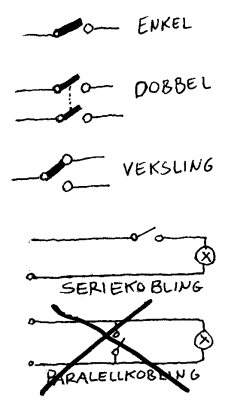 Den ene måten kalles seriekobling og den har vi beskrevet tidligere. Den andre måten kalles parallellkobling. En mulig beskrivelse av parallellkobling
er: Komponenter er koplet parallelt om tilført strøm deles opp før den går gjennom komponentene.
Den ene måten kalles seriekobling og den har vi beskrevet tidligere. Den andre måten kalles parallellkobling. En mulig beskrivelse av parallellkobling
er: Komponenter er koplet parallelt om tilført strøm deles opp før den går gjennom komponentene.
Hensikten med en bryter er å koble strøm til og fra komponenter eller elektrisk utstyr. Det skjer vanligvis ved at en strømleder brytes eller kobles sammen (enkel bryter). I noen tilfeller blir begge strømlederne mellom spenningskilden og det elektriske utstyret brudt i en bryter (dobbel bryter). En bryter kan også koble strømmen over fra en komponent til en annen (vekslingsbryter). Til høyre vises symboler for enkel bryter, dobbel bryter og vekslingsbryter
 Her vil vi konsentrere oss om de bryterne som bryter/kobler sammen en leder. Selv om vi bruker samme symbol på dem, så kan de fungere på to ulike måter. I en vanlig lysbryter kobler vi til strømmen i ett trykk og fra strømmen i et nytt trykk. Denne bryteren er altså stabil i både 'på' og 'av'-posisjonen og her kaller vi den bistabil bryter. I navnet ligger det at den er stabil i to ('bi') posisjoner. Bryteren til en ringeklokken leder derimot bare strøm så lenge man trykker på den. Denne bryteren er da bare stabil i 'av'-posisjonen. Denne bryteren kan vi da kalle monostabil bryter fordi den bare har en ('mono') stabil stilling.
Her vil vi konsentrere oss om de bryterne som bryter/kobler sammen en leder. Selv om vi bruker samme symbol på dem, så kan de fungere på to ulike måter. I en vanlig lysbryter kobler vi til strømmen i ett trykk og fra strømmen i et nytt trykk. Denne bryteren er altså stabil i både 'på' og 'av'-posisjonen og her kaller vi den bistabil bryter. I navnet ligger det at den er stabil i to ('bi') posisjoner. Bryteren til en ringeklokken leder derimot bare strøm så lenge man trykker på den. Denne bryteren er da bare stabil i 'av'-posisjonen. Denne bryteren kan vi da kalle monostabil bryter fordi den bare har en ('mono') stabil stilling.
Brytere skal alltid seriekobles Når en bryter er seriekoblet med det som skal ha strømmen vil den da bryte strømmen når vi slår den av slik hensikten var. Om vi derimot kobler en bryter parallelt med en komponent, vil bryteren representere "minste motstands vei" og stjele all strømmen fra komponenten. Det blir med andre ord en kortslutning. Vi kan ha mange brytere i elektrisk utstyr. Den bryteren som da kobler ut all strømmen kalles da hovedbryter.
 Kirchoffs lover
Kirchoffs lover1. lov
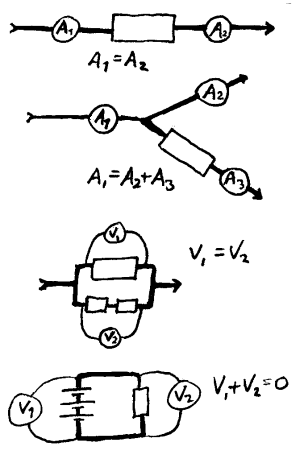
Denne lovmessigheten kan formuleres på ulike måter. En kortfattet, men kanskje litt uforståelig formulering er å si at det går like mye strøm inn og ut av et koplingspunkt. En mer praktisk formulering er vel å si at strømmen er den samme gjennom alle komponentene i en seriekopling. I et forgreningspunkt vil summen av inngående og utgående strøm være lik. En negativ formulering av det samme er å si at strøm ikke kan oppstå eller forsvinne i et punkt.
2. lov
Denne andre loven handler om spenning. En lovformulering er at spenningssummen langs ulike ledere mellom to koblingspunkt alltid er den samme. I en strømkrets betyr det at vi kommer tilbake til utgangspenningen når vi har beveget oss helt rundt, uansett hvilken vei vi har tatt. En negativ formulering kan da være at å si at et punkt ikke kan ha to ulike spenninger.
 Likestrøm og vekselstrøm
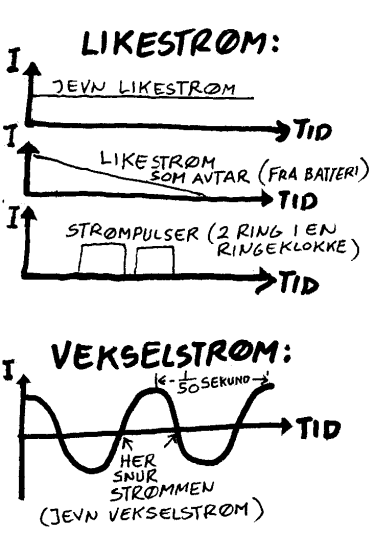
Likestrøm og vekselstrømLikestrøm (DC=direct current) kjennetegnes ved at strømmen går i samme retning hele tiden. Likestrøm kan variere i styrke og den kan også slås av og på slik som strømmen til en vanlig ringeklokken og signalstrømmene i datamaskiner. Dette kalles da opphakket likestrøm. Kurvene til høyre viser ulike likestrømmer i tid-retning-diagram og det som karakteriserer likestrøm er da at kurven alltid befinner seg på den ene siden av horisontalaksen. Kilder til likestrøm er batterier, batterieliminatorer/omformere og statisk elektrisitet.
Vekselstrøm (AC=alternating current) kjennetegnes ved at strømretningen veksler (fram og tilbake) vanligvis 50 ganger i sekundet. Det betyr at strømmen har en retning i ett øyeblikk, men i neste øyeblikk har strømmen motsatt retning. Kurven til høyre viser vekselstrøm i tid-retning-diagram. 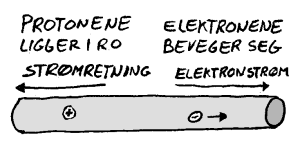 Når kurven er under horisontalaksen betyr det at strømretningen er motsatt av hva den var når kurva var over aksen. Tiden mellom en topp og neste topp i kurva er da en femtidel av et sekund i strøm fra lysnettet. Kilden til likestrøm er vanligvis generatorer/dynamoer. Spenningen til vekselstrømmen kan endres ved hjelp av en transformator.
Når kurven er under horisontalaksen betyr det at strømretningen er motsatt av hva den var når kurva var over aksen. Tiden mellom en topp og neste topp i kurva er da en femtidel av et sekund i strøm fra lysnettet. Kilden til likestrøm er vanligvis generatorer/dynamoer. Spenningen til vekselstrømmen kan endres ved hjelp av en transformator.
Mye og lite strøm
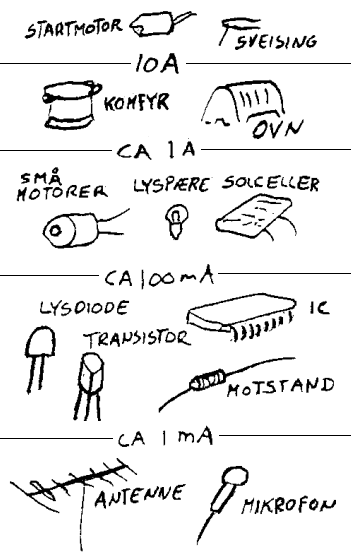
Benevningen eller enheten for strøm er Ampere (A) og det kan være nyttig å kjenne til noen kvantitative verdier som referanse når man arbeider med dette temaet i skolesammenheng.  Elektrisk strøm brukes i svært mange sammenhenger og det er da kjekt å vite litt om hvor mye strøm det er snakk om. I noen sammenhenger er det snakk om lite strøm (µA/mikroamper) og i slike tilfeller kan batterier vare fler år. Eksempler er klokker, måleinstrumenter ol. Selv batterier som ikke er tilkoblet en belastning vil bli utladet over tid og det betyr da at det også vil gå små strømmengder gjennom luft. På den andre siden brukes det svært store strømmengder i forbindelse med sveising og annen oppvarming til høye temperaturer. Her er det da snakk om noen flere titalls A. I skolen kan vi demonstrere hva som skjer ved store strømmengder hvis man har en større transformator som transformerer spenning fra 220V til f.eks. 3V. Hvis vi da kortslutter utgangen på en slik transformator med f.eks. en spiker vil vi kunne oppleve at spikeren smelter fordi det går så mye strøm gjennom den. De fleste skoler har svietransformatorer for å brenne inn tekst og bilder i tre og en slik transformator kan da brukes til å brenne av en tynn metalltråd.
Elektrisk strøm brukes i svært mange sammenhenger og det er da kjekt å vite litt om hvor mye strøm det er snakk om. I noen sammenhenger er det snakk om lite strøm (µA/mikroamper) og i slike tilfeller kan batterier vare fler år. Eksempler er klokker, måleinstrumenter ol. Selv batterier som ikke er tilkoblet en belastning vil bli utladet over tid og det betyr da at det også vil gå små strømmengder gjennom luft. På den andre siden brukes det svært store strømmengder i forbindelse med sveising og annen oppvarming til høye temperaturer. Her er det da snakk om noen flere titalls A. I skolen kan vi demonstrere hva som skjer ved store strømmengder hvis man har en større transformator som transformerer spenning fra 220V til f.eks. 3V. Hvis vi da kortslutter utgangen på en slik transformator med f.eks. en spiker vil vi kunne oppleve at spikeren smelter fordi det går så mye strøm gjennom den. De fleste skoler har svietransformatorer for å brenne inn tekst og bilder i tre og en slik transformator kan da brukes til å brenne av en tynn metalltråd.
 Nå vet alle at strøm kan være farlig for oss mennesker. En strømmengde på 80mA vil f.eks. være dødlig om vi får den gjennom kroppen.
Nå vet alle at strøm kan være farlig for oss mennesker. En strømmengde på 80mA vil f.eks. være dødlig om vi får den gjennom kroppen. 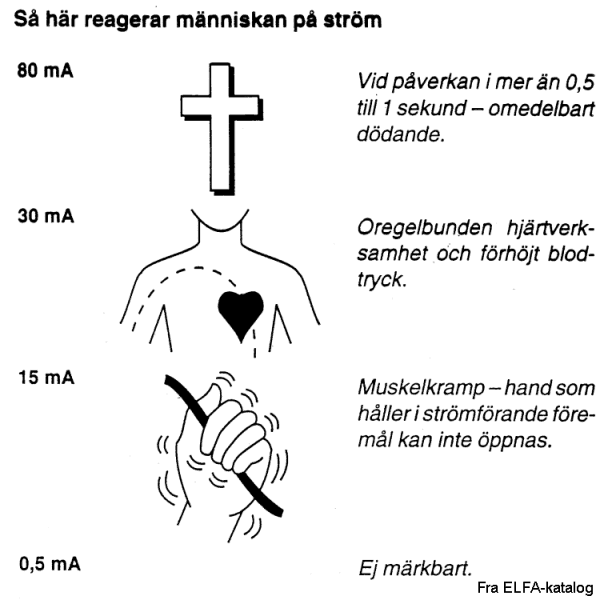 Grensen for at vi får muskelkrampe (ikke kan styre musklene selv) er ca. 15mA og grensen for at vi kjenner/føler strømmen er ca. 0,5mA. Om vi med fingrene tar på et lommelyktsbatteri på 4,5V vil det kanskje gå 0,1-0,2mA gjennom fingrene våre. I ei vanlig lommelykt vil det til sammenlikning gå en strøm på 200-300mA mens en elektromotor i en kassettspiller vil bruke endel mindre. Ei solcelle gir fra seg 100-700mA. En lysdiode trenger på sin side mindre enn 1mA for å lyse, men de får da 10-40mA når de lyser normalt. Ellers vil strømstyrken i mikrofoner, antenner og andre følere/sensorer som skal fange opp signaler utenfra være godt under 1mA. Som en tommelfinger-regel kan vi si at det trenges over 100mA for at vi skal ha noen særlig nytte utad i form av lys eller bevegelser. Internt i elektriske kretser vil vi av energimessige hensyn søke å holde strømstyrkene godt under 100mA. Derfor passer lysdioder godt til å indikere hva som skjer i disse kretsene. Mye elektronisk utstyr er ellers beregnet på å fange opp svake signal som har strømstyrker langt under 1mA. Signaler fra mikrofoner og antenner må da forsterkes for at vi skal ha nytte av disse.
Grensen for at vi får muskelkrampe (ikke kan styre musklene selv) er ca. 15mA og grensen for at vi kjenner/føler strømmen er ca. 0,5mA. Om vi med fingrene tar på et lommelyktsbatteri på 4,5V vil det kanskje gå 0,1-0,2mA gjennom fingrene våre. I ei vanlig lommelykt vil det til sammenlikning gå en strøm på 200-300mA mens en elektromotor i en kassettspiller vil bruke endel mindre. Ei solcelle gir fra seg 100-700mA. En lysdiode trenger på sin side mindre enn 1mA for å lyse, men de får da 10-40mA når de lyser normalt. Ellers vil strømstyrken i mikrofoner, antenner og andre følere/sensorer som skal fange opp signaler utenfra være godt under 1mA. Som en tommelfinger-regel kan vi si at det trenges over 100mA for at vi skal ha noen særlig nytte utad i form av lys eller bevegelser. Internt i elektriske kretser vil vi av energimessige hensyn søke å holde strømstyrkene godt under 100mA. Derfor passer lysdioder godt til å indikere hva som skjer i disse kretsene. Mye elektronisk utstyr er ellers beregnet på å fange opp svake signal som har strømstyrker langt under 1mA. Signaler fra mikrofoner og antenner må da forsterkes for at vi skal ha nytte av disse.
 Faremomenter
ved bruk av elektrisitet
Faremomenter
ved bruk av elektrisitet
Det er mye strøm er farlig! (ikke høy spenning)
Eksempel på ufarlige høye spenning er det vi kan få fra en
coil. Bildet til venstre viser en enkel kobling som gjør at man kan kjenne
høye spenninger uten at det er farlig. Det er da høy spenning
kombinert med mye energi som er farlig for mennesker. Dette vil da gi mye strøm
gjennom kroppen. Et eksempel: Fuktige fingrer gir ca 30kW Strøm gjennom
kroppen blir da: I=U/R=220V/30kW=7mA
 Elektromotorisk spenning (EMS)
Elektromotorisk spenning (EMS)
Det som gjør at det blir en spenning mellom polene i et batteri eller en annen strømkilde kalles ofte elektromotorisk spenning. Her vil vi bare nevne at denne spenningen som regel er litt større enn den polspenningen vi måler når batteriet leverer strøm. Årsaken til denne forskjellen er da at det i batteriet vil være en slags indre resistans (Ri) som i praksis gjør at det er grenser for hvor store strømmengder ulike batterier kan levere. I praktiske forsøk er det mer praktisk å snakke om polspenning i stedet for EMS, og det er da viktig at vi er klar over at polspenningen avtar når belastningen øker. Sammenhengen mellom EMS(e) og polspenning(Vp) er: Vp=e-RiI
 Bruk av Ohms lov
Bruk av Ohms lov
Ohms lov forteller at resistans er forholdet mellom spenning og strøm: R=V/I. Vi har tre størrelser hvorav en av disse kan bestemmes når de to andre er kjent. Denne sammenhengen kan settes opp på 3 ulike måter. De fleste velger å huske den første og så utledes de andre fra denne:
V=RI I=V/R R=V/I
Ohms lov er grunnleggende i all elektronikk og elektrisitetslære. I tillegg til at formelen kan brukes til å finne en verdi når to andre er kjent, sier også formelen noe om hva som skjer hvis vi endrer på noen av verdiene. Om vi f.eks. over en motstand (med fast resistans) øker spenningen vil også strømmen øke. Om vi et annet sted minker resistansen mens spenningen holdes konstant, vil strømmen øke.
 Hvordan bruke ohms lov?
Hvordan bruke ohms lov?
Slik som ohms lov er presentert ovenfor, virker den enkel. Praksis har imidlertid vist at den ikke er så enkel som den ser ut. Det er derfor ikke bare å pugge formelen ovenfor, og så tro at det er nok. Her følger noen eksempler på bruk av ohms lov. Generelt vil vi her si at det er viktig å gjøre ulike oppgaver for å få øving i å anvende ohms lov.
Anta en strømkrets med pære og et batteri på 4,5 V. Målinger med amperemeter viser da kanskje en strømstyrken på 250 mA. Ved hjelp av Ohms lov kan vi da beregne resistansen R = V/I = 4,5/0,25 = 18W. Om vi f.eks. kopler en motstand på 33 O i serie med pæra vil vi se at den nesten ikke lyser. Hvis vi vil finne ut hvor mye strøm som går gjennom pæra etter omkoblingen, kan vi også bruke Ohms lov. 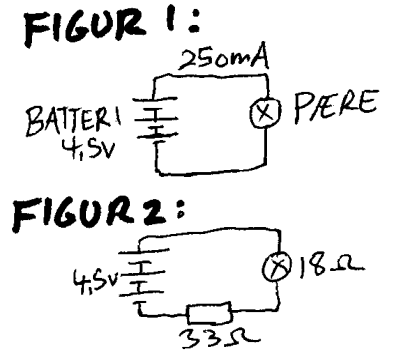 Vi vet at resistansen i pæra var ca 18W og til sammen vil resistansen bli 51 O. Strømmen i begge komponentene til sammen blir da I = V/R = 4,5V/51W = 88 mA. Merk at både spenning og resistans kan summeres om vi måler dem over flere komponenter som er koplet i serie. Strømmen er da den samme i alle seriekoblede komponenter (Kirchoffs 1 lov).Om vi så ønsker å vite spenningen over pæra kan vi også bruke ohms lov, men da kun over pæra. Vi vet at strømmen gjennom pæra er like stor som gjennom de andre komponentene når de er koplet i serie. Vi får derfor følgende:
Vi vet at resistansen i pæra var ca 18W og til sammen vil resistansen bli 51 O. Strømmen i begge komponentene til sammen blir da I = V/R = 4,5V/51W = 88 mA. Merk at både spenning og resistans kan summeres om vi måler dem over flere komponenter som er koplet i serie. Strømmen er da den samme i alle seriekoblede komponenter (Kirchoffs 1 lov).Om vi så ønsker å vite spenningen over pæra kan vi også bruke ohms lov, men da kun over pæra. Vi vet at strømmen gjennom pæra er like stor som gjennom de andre komponentene når de er koplet i serie. Vi får derfor følgende:
U = RI = 18W*88mA = 1,6V.
Merk at resistansen i pæra endrer seg med temperaturen i glødetråden. Videre vil spenningen over batteriet (polspenningen) endre seg når vi belaster batteriet. Derfor er tallene ovenfor unøyaktige. Merk også at så store strømmer som 80 mA utvikler varme og motstanden blir derfor relativt varm. Komponenter som ikke er beregnet på så store strømmer kan bli for varme og ødelegges.
 Beregning av strøm i seriekoblinger og parallellkoblinger
Beregning av strøm i seriekoblinger og parallellkoblinger
I oppgaver om elektrisk strøm er det vanlig med oppgaver hvor vi nå beregne totalresistansen eller erstatningsresistansen (Rt) over flere resistanser (R1, R2). I disse tilfellene er sammenhengen som følger.
Ved seriekopling: Rt = R1 + R2
Ved parallellkobling: 1/Rt = 1/R1 + 1/R2
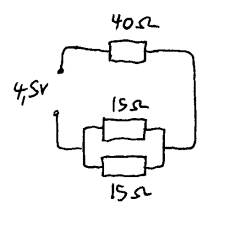
Oppgaveeksempel: Finn totalresistans og strøm og effekt i eksempelet som er vist til høyre.
Løsningsforslag: Vi finner først resistansen over parallellkoblingen Rp:
1/15W + 1/15OW= 1/Rp
Rp = 10W
I seriekobling kan vi summere resistanser og får totalresistansen:
Rt = 10W + 40W = 50W
Bruker så ohms lov for å finne strømmen:
I = V/R = 4,5V/50O = 90mA
Bruker så effektformelen for å finne totaleffekten:
P = VI = 4,5V*90mA = 0,4W
 Måling av strøm og spenning
Måling av strøm og spenning
Ved hjelp av et rimelig multimeter er det enkelt å måle både strøm og spenning i praktiske situasjoner. Ved hjelp av en bryter på multimeteret kan vi gjøre multimeteret om til ampermeter, voltmeter og annet. Her følger noen tips i denne sammenhengen.
Amperemeter er et instrument som bruktes til å måle strømstyrke. Det har selv liten indre resistans og vil derfor slippe gjennom mye strøm. Når vi skal måle strømmen i en strømkrets med en amperemeter, må vi bryte kretsen og koble ampermeteret i serie. Hvis et amperemeter kobles parallelt vil det kunne kortslutte kretsen og både ampermeteret og komponenter i kretsen kan bli ødelagt.
Voltmeter er et instrument som brukes til å måle elektrisk spenning. Det har stor indre resistans. Det går derfor minimalt strøm gjennom det. Voltmeteret skal koples parallelt med de komponentene vi vil finne spenningen over. Når vi bruker voltmeter slipper vi altså å bryte strømkretsen. Siden det går så lite strøm gjennom voltmeteret, vil det ikke forstyrre kretsen nevneverdig. Derfor er det også små sjanser for å ødelegge voltmeteret eller nærliggende komponenter ved eventuelle feilkoplinger. 
 1.7 (31.03.95) Nevn flest mulig ulike prinsipp som kan skape elektrisk spenning mellom to punkt.
1.7 (31.03.95) Nevn flest mulig ulike prinsipp som kan skape elektrisk spenning mellom to punkt.
2.1 Når vi kobler en strømkrets til et batteri, vil elektroner strømme fra den negative til den positive polen. Hvorfor blir det da ikke overskudd av elektroner på den positive polen slik at den blir negativ?
2.2 Sett kryss når pæra lyser i figurene til bøyre.
[ ] A [ ] B [ ] C
[ ] A [ ] B [ ] C
[ ] D [ ] E [ ] F
[ ] D [ ] E [ ] F
[ ] G [ ] H [ ] I
[ ] G [ ] H [ ] I
[ ] J [ ] K [ ] L
[ ] J [ ] K [ ] L
2.3 Motstander kan brukes i elektriske kretser for å regulere strøm og spenning.
a) Tegn elektrisk skjema for en strømkrets hvor en variabel motstand kan endre lyset i ei lyspære.
b) Gi en kort beskrivelse av ohms lov med ord og symboler.
c) Bruk ohms lov til å forklare hvorfor lysstyrken i pæra endrer seg.
2.4 Batteriet levere mest strøm når: (stryk det som er feil)
a) Når vi bruker en lang eller kort leder? b) Når vi bruker en tykk eller tynn leder?
c) Når vi bruker kobbertråd eller jerntråd? d) Når vi bruker enkle ledere eller doble ledere?
e) Når vi kobler to pærer i serie eller parallelt?
2.5 (12.86) a) Hva er strøm? b) Forklar hvorfor en motstandstråd kan gløde samtidig som en vanlig leder ikke blir varm selv om det går samme strømmen gjennom dem begge.
2.6 (12.86) Du har to batterier (4,5V) og to pærer (som tåler max 6V). Hvordan ville du koblet dem for at a) begge pærene skal lyse lengst mulig og b) begge pærene skal lyse mest mulig.
2.7 (12.86) Forklar forskjellen på vekselstrøm og likestrøm. Hva er fordelen med de ulike strømtypene.
2.8 (05.90) Elektrisitet er både nyttig og farleg. a) Forklar omgrepa straum og spenning. b) Gje nokre eksemplar på ulike verdiar for straum og spenning og sei óg noko om kor store verdiar som må til for at det er vondt og farleg å ta på.
2.9 (9.12.91) Nevn minst 3 ulike prosesser/prinsipp som kan gi spenning og strøm. Beskriv forsøk som kan demonstrere dette for elever.
2.10 (25.02.94) Forklar begrepene strøm og spenning.
Hva er forskjellen og hva er farlig? Gi eksempler.
2.11 (31.03.95) Forklar virkemåten til bandgeneratoren (Van de Graf-generatoren). Hva slags krefter oppstår? Gi eksempler på demonstrasjonsforsøk hvor vi bruker bandgeneratoren.
2.12 (31.03.95) En elektrolyttkondensator kan lades opp. Så kan vi bruke energien i kondensatoren til å få en diode til å lyse. Tegn og forklar fremgangsmåten for å demonstrere dette. Nevn andre bruksmåter til en kondensator.
2.13 Når tror du batteriet belastes mest (=leverer mest strøm)?
1)Når to pærer er koplet i serie eller
2)når de er koplet parallelt til batteriet. Argumenter utfra Ohms lov. (løsningsforslag)
2.14 Hva er kortslutning og hvorfor kan det medføre brann i f.eks. en bil.
2.15 (31.03.95) Forklar hva vi mener med elektrisk strøm. Når oppstår strøm og hvordan kan vi påvise strøm?
2.16 (5.12.95) Forklar ordene motstand, resistans og ohm(W). Hva skiller atomene i en leder fra atomene i en motstand?
2.17 (5.12.95) Forklar begrepene likestrøm og vekselstrøm.
2.18 (23.1.96) Hvordan vil du forklare hva som ligger i begrepene strøm og spenning for elever i grunnskolen?
3.9 (5.12.95) Hva er et batteri, og hva driver elektronene fra - polen til + polen?
4.1 Beregn resistansen i en 15W og en 60W pære beregnet på 220V.
Beregn også resistansen i en 15W pære beregnet på 12 V.
4.2 En motstand på 1W og en på 9W koples i serie og parallelt. Hva blir erstatningsresistansen i de to tilfellene?
4.3 Vil en 60W pære lyse når den kobles til et batteri på 4,5V? Argumenter utfra U=RI og P=UI.
4.4 Anta to batteri (4,5V) og to pærer (som tåler max 6V). Hvordan ville du koble dem for de skal
a) lyse lengst mulig
b) skal gi mest mulig lys.
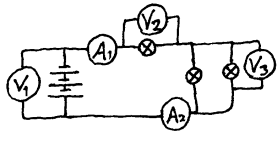 4.5 a) Hva viser V2 når V1 viser 4,2 og V3 viser 1,5.
4.5 a) Hva viser V2 når V1 viser 4,2 og V3 viser 1,5.
b) Hva viser A2 når A1 viser 0,2.
4.6 Lampene i kretsen er like. Vi skrur ut (c). Vil (a) lyse sterkere eller svakere? Vil (b) lyse sterkere eller svakere?
4.7 Ei kokeplate står på 1000W. Hva er strømmen?
4.8 Hvor mange W kan vi sette panelovner tilkoplet en 10 A sikring på?
4.9 Anta 220V og 60 W for ei lyspære. Bruk P=UI og U=RI for å bestemme resistansen når pæra lyser. Mål også resistansen med multimeter. Kommenter resultatet.
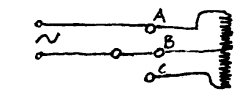 4.10 Glødetrådene mellom A og B og mellom B og C er like lange. Når bryteren står på B er effekten 500W. Hva blir effekten om bryteren står på C. Hva ville skje om bryteren kunne koples til A?
4.10 Glødetrådene mellom A og B og mellom B og C er like lange. Når bryteren står på B er effekten 500W. Hva blir effekten om bryteren står på C. Hva ville skje om bryteren kunne koples til A?
4.11 På et strykejern står det 220V og 800W. Beregn strøm og resistans.
4.12 (12.86) På ei pære står det: 3,8 V og 0,3 A. Kor stor er motstanden i denne pæra? Hva blir straumen dersom vi koplar denne pæra til eit 4,5 V batteri og ser bort frå motstand i batteriet og i ledningane. Ein straumstyrke på 0,02 A kan vere farlig å få gjennom kroppen. Forklar kvifor denne koplinga ikkje er farlig når det går meir straum gjennom den.
4.13 (05.88) a) Figuren viser eit 4.5V batteri, ein elektromotor, ein visp og eit glass med vatn. Forklar energitransporten når dei er kopla slik figuren viser. Kva for energitypar er med og kva omdannes desse til?
b) Hvis ein lar oppstillinga stå to timar og beregnar motstanden til å vere 10 ohm. Kva er då effekten hvis ein antar polspenninga på batteriet ikkje vert redusert noko serleg på grunn av belastningen?
Kor mykje energi er overført på denne tida?
Kor mykje varmare blir vatnet etter desse to timane dersom ein antar at all energien blir verande i vatnet. Glasset inneheld 1,5 dl vatn, og varmekapasiteten til vatn er 4,2 kJ/kg*K.
c) Vil vatnet bli varmare eller kaldare dersom ein erstattar motoren med ei pære som brukar like mykje straum og senker henne ned i vatnet? Begrunn svaret.
4.14 På et bilbatteri står det 12V og 60Ah. Det siste betyr f.eks. at det kan levere 1A i 60 timer etter at det er fullt oppladet. Anta at frontlysene og alle baklysene (skiltlys+to bakklys) til sammen er på 150W.
-Hvor mye energi kan batteriet maksimalt gi?
-Hvor lenge kan billysene stå på før batteriet er utladet.
4.15 (9.12.91) a) Er spenningen mellom polene på et batteri alltid det som står på batteriet? Hva er det som gjør at polspenningen kan variere.
b) Et vanlig flatt lommelyktsbatteri på 4,5V vil i ei vanlig lommelykt beholde påtrykket spenning og levere ca 230mA når batteriet er nytt. Hva er motstanden i pæra, og effekten i lommelykta.
c) Om vi kopler det samme batteriet til en kassettspiller vil effekten her med moderat lydnivå være ca. 0,4W. Hvor mye strøm trekker kassettspilleren?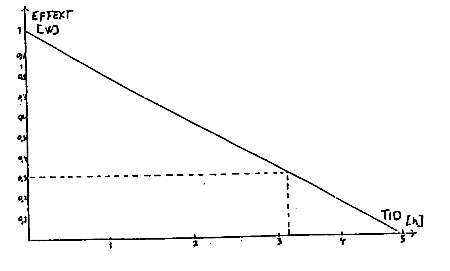 d) Vi antar at noen barn vil legge inn elektrisitet i ei hytte. De henger ei vanlig lommelyktspære(3,5V 0,2A) under taket, og bruker et vanlig flatt lommelyktsbatteri som energikilde. Om batteriet i starten gir en effekt på 1W viser kurven nedenfor at effekten etter vel 3 timer vil være nede i ca 0,3 W som vi her kan anta er en grense for at taklyset er til noe hjelp. Om vi fortsatt lar den være tilkoplet vil vi kunne se at den gløder til effekten kommer ned i ca. 0,1 W. Hvor lang tid vil vi utfra kurva kunne se lys i pæra. Om vi antar at den indre motstanden i pæra er konstant hele tiden kan vi si noe om strøm og spenning etter som tida går. Hva skjer da med polspenningen til batteriet over tid, og hvor stor vil den være når effekten i pæra er 0,3W.
d) Vi antar at noen barn vil legge inn elektrisitet i ei hytte. De henger ei vanlig lommelyktspære(3,5V 0,2A) under taket, og bruker et vanlig flatt lommelyktsbatteri som energikilde. Om batteriet i starten gir en effekt på 1W viser kurven nedenfor at effekten etter vel 3 timer vil være nede i ca 0,3 W som vi her kan anta er en grense for at taklyset er til noe hjelp. Om vi fortsatt lar den være tilkoplet vil vi kunne se at den gløder til effekten kommer ned i ca. 0,1 W. Hvor lang tid vil vi utfra kurva kunne se lys i pæra. Om vi antar at den indre motstanden i pæra er konstant hele tiden kan vi si noe om strøm og spenning etter som tida går. Hva skjer da med polspenningen til batteriet over tid, og hvor stor vil den være når effekten i pæra er 0,3W.
e) Utfra den samme kurva kan vi da se at den totale energien i batteriet som tilsvarer arealet under kurva er 1W*5*60*60s*½=9kJ=2,5Wh (areal av en trekant er lik høyde*grunnlinje*½) Vi antar at en kassettspiller maksimalt trekker 0,4W og trenger minimalt 0,3W for å virke brukbart. Kan du anslå noe om hvor lenge den ville virke om vi koplet den til batteriet i stedet for pæra som er nevnt ovenfor.
f) Om vi antar at et 4,5V lommelyktsbatteri koster kr 20,- og det leverer en energimengde på 0,0025kWh så vil 1 kWh koste kr 8000.- Når E-verket tar ca kr 0,50 for hver kWh er det ikke så vanskelig å innse at batterier blir en dyr energikilde i hytta. Barna finner derfor ut at de vil skaffe "gratis" energi fra en nærliggende bekk. De lager et energiverk v.h.a. en sykkeldynamo og finner ut at dette energiverket leverer maksimalt 1W. Hva gjorde de for å finne ut effekten og hvor lenge må dette energiverket gå for å levere en kWh?
g) Siden sykkeldynamoen leverer vekselstrøm må den likerettes før den kan brukes til å drive kassettspilleren. Anta at likespenningen som når hytta er 4,5 V når barna kopler til bare ei pære. Hva vil det si å kople to pærer i serie og parallelt. Hva tror du vil skje med spenningen inn i hytta i disse to tilfellene. Hvor mange pærer tror du det er mulig å kople parallelt med kassettspilleren uten at kassettspilleren blir falsk.
4.16 (16.12.93) To ulike pærer vil henholdsvis trekke 80mA (pære A) og 50mA (pære B) når de koples direkte til et 4,5V batteri.
-Tegn en seriekopling og en parallellkopling med disse pærene. Anta videre at vi kopler en motstand på 20W inn i en strømkrets med et batteri og de to ovennevnte koblingene.
-Beregn strøm og spenning over pærene i tilfellet med parallellkobling av pærene og i tilfellet med seriekopling av pærene. Anta at motstanden i pærene er konstant.
4.17 (25.02.94) Ei vanlig lommelyktspære vil trekke ca 220mA fra et 4,5V batteri.
-Hva er da motstand og effekt i pæra i dette tilfellet.
Ei pære som er beregnet på høyere spenning vil f.eks. trekke 0,4W når den koples til det samme batteriet. Hva er strøm og motstand i dette tilfellet?
-Beregn effekten i de to pærene når de er tilkoplet det samme batteriet i serie og parallelt (4 tall).
4.18 (12.94) Hvilken pære lyser sterkest når vi seriekobler ei på 40W og ei på 60W til lysnettet (220V). Begrunn svaret. Hva blir totaleffekten (P) når de er seriekoblet. (svareksempler)
4.19 (12.94) Vi har en strømkilde på 4,5V (batteri eller batterieliminator), en regulerbar motstand på 0-150W og to like pærer. Når alle komponentene er seriekoblet og den regulerbare motstanden står på 5W går det en strøm i kretsen på 100mA. Hva må vi stille den regulerbare motstanden på om vi heller vil parallellkoble pærene og samtidig ønsker at de skal lyse like mye som i det første tilfellet.
4.20 (31.03.95) Vi har et batteri på 4,5V og to pærer. Tegn både en seriekobling og en parallellkobling hvor pærene lyser. Anta at pærene har en resistans på 45W når de lyser. Finn totaleffekten i begge tilfellene.
4.21 (31.03.95) Vi har en strømkilde på 12V (bilbatteri), en regulerbar motstand på 0-150W og en bilpære på 5W (kupelys) og en pærer på 21W (bremselys). Vi kobler den regulerbare motstanden inn i en krets sammen med en av de to pærene og vrir på motstanden. Så gjør vi det samme med den andre pæra. Når får vi maksimal strøm gjennom den regulerbare motstanden? Hva er den minimale strømmen gjennom den regulerbare motstanden?
4.22 Hva er motstanden i ei vanlig 40W pære som vi kopler til lysnettet? Bruk formlene P(effekt)=UI og U=RI. Har ei 60W pære større eller mindre motstand. Hvilke pære lyser mest av ei på 60W og ei på 40W når det koples parallelt og i serie? Hvorfor?
4.23 (5.12.95) På en sykkel kobler vi tre pærer parallelt til en dynamo som vi antar gir 3W. Pæra i hovedlyset skal da gi 2W, bremselyspæra 0,6W og baklyspæra 0,4W.
a) Tegn et koblingsskjema som viser dynamo, pærer og brytere for lys og bremselys. (Bremselyset skal virke uavhengig av bryteren til de andre lysene)
b) Anta at dynamoen gir 6 V. Finn da motstanden i de tre pærene. (løsningsforslag)
4.24 Tegn koblinger og finn strøm og spenning over ei pære på 40W og ei på 60W når de kobles til lysnettet (220V)
a) parallelt. b) i serie.
4.25 Vi har et batteri på 4,5V og ei pære som lyser med 1W.
a) Finn strøm og motstand i pæra.
b) I serie med den første pæra kobler vi så inn en paralellkobling med to pærer som er lik den første. (3 pærer totalt). Tegn koblingen og beregn strøm og spenning i forbindelse med alle pærene (6 tall).
c) Lag en oversikt som viser hva som skjer med lyset i de to andre pærene om en pære går. Si både hva som skjer hvis pærene går som følge av strømbrudd (R=¥
) eller som følge av at de kortsluttes (R=0). (6 muligheter hvor det skal sies noe om to andre pærer vil lyse mer, like mye eller mindre enn før)
Løsningsforslag
1.7 Strøm / spenning kan oppstå som følge av:
1 GNIDNING: mellom f.eks. glasstav og plast. Vi kan se gnister i mørke og høre dem i lyset.
2 KJEMISKE REAKSJONER: I et batteri er det kjemiske reaksjoner som skaper ulik spenning på polene og gir strøm. Demoeksempel: Sink og kopper i ei potet kan gi utslag på ampermeter.
3 INDUKSJON: I generatorer oppstår strøm i spoler fordi magnetfeltet i nærheten endrer seg. Demonstrere induksjon v.h.a. en spole (10 000 vindinger), en magnet og lysdiode/ ampermeter.
4 SOLCELLE I ei solcelle vil lys føre til at det oppstår spenninger uten at det skjer noen kjemiske reaksjoner. Ei solcelle kan gi nok strøm til spesielle elektromotorer.
2.1 Det skjer en tilbakeføring av elektroner inni batteriet som følge av kjemiske prosesser
2.2 d, g og k lyser i begge seriene.
Resultat fra en 6. klasse:
000100 100010 000100 100010-fasit
010100 010010 001100 100010-1
010100 101011 011100 101011-2
000110 101011 001100 001101-3
000100 100010 000100 100011-4
010100 110110 011100 101011-5
010100 110110 011011 010011-6
100110 011010 011100 101011-7
101100 101010 011100 101011-8
011000 101011 011100 101001-10
110001 101010 110010 001100-11
011100 101010 011100 101011-12
000100 100010 000100 100010-13
011100 110001 000100 100111-14
100100 111000 011100 101001-15
010100 100111 011100 111110-16
010001 010001 110111 000101-17
011100 100011 010100 100000-18
010100 100001 001100 010001-19
101101 010011 101111 000001-20
011000 101001 011100 101011-21
000100 100010 010100 110010-22
000100 100011 000100 100011-23
011100 101011 011100 101010-24
110100 101010 001101 101101-25
2.5 Elektrontransport / elektroner som beveger seg i samme retning. I en leder vil mange elektroner bevege seg sakte og kort. I en motstandstråd vil få elektroner bevege seg fort og langt og forårsake varme fordi de avgir varmestråling hver gang de stopper opp (retarderes).
2.6
Lengst mulig:+-+---+ Mest mulig:+-+-+-+
¦
¦ ¦ ¦
¦ ¦ ¦
B B P B B P P
¦
¦ ¦ ¦
¦ ¦ ¦
+-+-P-+
+-+-+-+
2.7 Likestrøm: Elektronene beveger seg i kun en retning Vekselstrøm: Elektronene beveger seg vekselvis fram og tilbake. Likestrøm nødvendig i mye elektronikk. Vanligvis får vi vekselstrøm fra generatorer og det er lett å endre spenning til vekselstrøm (i transformator) og lyspærer lyser lenger når de få vekselstrøm.
2.13 Størst belastning ved paralellkopling. Minst resistans ved paralellkobling => størst strøm.
2.14 Svært liten resistans i en strømkrets. Eksempler: Direktekontakt mellom batteripoler. Strøm vil velge "minste motstands vei" og går utenom komponenter om det oppstår "overledning". Ved kortslutning går det mye strøm som i sin tur kan utvikle varme som så kan ødelegge komponenter eller forårsake brann.
2.16 Svareksempel:
"Atomene i en leder er lett bevegelige, mens atomene i en motstan er tungt bevegelige"
2.17 Svareksempler:
"Mens i vekselstrøm kan elektrona bevege seg fram og tilbake"
"Vekselstrøm Elektronene i en leder går i "alle" retninger."
"Vekselstrøm: elektroner skifter retning hele tiden gjennom en leder (elektromotor)."
"Ei stikkontakt med vekselstraum ville då ha veksla ml å vere positiv (+) og negativ (-)."
"*Likestrøm -strømmen går en veg inni ledningen. (tegnet med piler en veg) *Vekselstrøm - strømmen veksler, den går begge veger. (tegnet en leder med piler begge vegen)."
"Likestrøm: Strømmen går jamnt utan større svingningar, ein kan difor som i ei lommelykt, ha svake batteri, men ikkje blinking i pæra.
Vekselstrøm: Strømmen går i bølgjer (tegnet en bølge), veksler frå topp til bunn. Ved f.eks. svak vekselstrøm vil vi derfor merke blinking i ei pære. Det blir 'lang tid' mellom bølgjene."
3.1 Svareksempler: 'På dette tidspunktet vil strømmen bli brutt og det er bare de magnetiske kreftene som virker....(De magnetiske kreftene har sluttet å virke og de elektriske tar over)'
'For å forstå ein elektromotor må elevane tidligare ha hatt om vekselstraum..'
4.1 R=U/I=U²/P=220²/15W=3200W R=220²/60=810W
R=12²/15=9,6W
4.2 10W og 0,9W
4.3 Nei Resistans i pæra er:R=U/I=U²/P=800W. Strømmen vil da bli I=U/R=5mA som er for lite til å varme opp glødetråden.
4.4 a)Batteriene parallellt. Pærene i serie b)Alt i serie eller alt parallelt.
4.5 a)2,7V b)0,2A
4.6 A vil lyse svakere fordi spenningen over a blir mindre.
4.7 I=P/V=1000W/220V=4,5A
4.8 Maksimaleffekt: P=UI=220V*10A=2200W
4.9 R=U/I=U²/P=800W Målt:50W Resistansen øker ved oppvarming.
4.10 250W (Resistansen dobles og effekten (P=UI=U²/R) blir halvert) Tilkobling til a betyr kortslutning
4.11 3,6 A og 60 W
4.12 R=U/I=12W I=U/R=370mA NB! Motstanden avhenger av temperaturen til glødetråden og ei lyspære har derfor ikke fast motstand.
4.13 b) P=U²/R=2W E=Pt=2W*2*60*60=14kJ
c) Temperaturforskjell: 14kJ / 4,2kJ/kgK * 0,15kg = 22K
4.15 a) Polspenningen er ofte litt mer enn oppgitt spenning når det ikke belastes. Normal belastning gir ofte at polspenningen er lik oppgitt spenning. Når man trekker for mye strøm ut av et batteri vil polspenningen bli mindre enn oppgitt. Det samme skjer også når batteriet blir gammelt.
b) Motstanden i pæra R= U/I = 4,5V/230mA = 20W
Effekten i lommelykta: P=U*I = 4,5V*230mA = 1,0W
c) Antar polspenning på 4,5 V
Strøm gjennom kassettspilleren: I = P/U = 0,4W/4,5V = 89mA
d) Kurva viser at vi vil se at pære gløder i ca. 4,5 timer. Om indre motstand i pæra er konstant vil både spenning og strøm avta når effekten minker (P=UI og U=RI)
Vi kjenner hverken U eller I men bare P og R. Vi må derfor kombinere formlene ovenfor. Hvis vi finner I i ohms lov og setter den inn i effektloven får vi:
P = U * U/R => U² = P*R
U=Ö
PR = Ö
0,3*20 V = 2,4 V
e) Figuren viser at energien som kan leveres før effekten er falt til under 0,3W er 2,5Wh-0,3*2*½Wh=2,1Wh (trekker fra den lille trekanten til høgre). Om vi så antar at kassettspilleren i gjennomsnit trekker 0,35 W får vi utfra formelen E=Pt:
Tid før batteriet er utbrukt: t=E/P=2,1Wh/0,35W=6h
(Dette er et grovt overslag. Overslag direkte fra figuren godtaes også)
f) Maksimal effekt finner vi ved å belaste anlegget endel slik at spenningen begynner å synke, og så måle strøm og spenning. Effekten er da produktet.
Energiverket har levert 1kWh etter t=E/P=1kWh/1W=1000h=42døgn
g) Figuren viser paralellkopling og seriekopling. Generelt vil spenningen minke når belastningen øker (totalresistansen blir mindre). Derfor vil nok spenningen inn i hytta være litt høyere ved seriekopling enn paralellkopling.
Når kassettspilleren bruker 0,3W er det 0,7 W igjen til pærene. Nå kjenner vi ikke minimal spenning som kasettspilleren må ha for å virke. Ovenfor så vi at ei pære kan gi litt lys med en effekt på 0,3 W. Spenningen var da 2,4V. Hvis kasettspilleren fungere på 2,4 V kan vi i prinsippet tenke oss at total-effekten deles på tre. Dvs to pærer pluss kassettspiller. Det er kanskje mest sannsynlig at en kassettspilleren av den typen som vi brukte som er beregnet på 6V trenger høyere spenning. Derfor er det mest sannsynlig at det bare er ei pære som kan skinne sammen med kasettspilleren (eller ingen).
4.16 Resistanser Ra=U/I=4,5V/80mA=56W Rb=U/I=4,5V/50mA=90W
+--X--+
+-¦|--==--¦ +--+ +-¦|--==--X--X-+
¦ +--X--+ ¦ ¦
¦
+------------------+ +--------------+
Paralellkopling: 1/Ra + 1/Rb = 1/Rp 1/56W + 1/90W = 1/Rp Rp=35W
Rt=20W+35W=55W
I=U/Rt=4,5V/55W=82mA
Ur=RI=20W*82mA=1,6V
Seriekopling: Rt=20W+56W+35W=110W
I=U/Rt=4,5V/110O=41mA
Ur=RI=20O*41mA=0,8V
4.18 R40=U/I=U²/P=(220V)²/40W=1200W
R60=U/I=U²/P=(220V)²/60W=807W
Lik strøm + mest spenning over 40W (U=RI) => Størst effekt over 40W (P=UI)
Totaleffekt P=UI=U²/R=(220V)²/(1200+807)O=24W
Svareksempler: 'Pæra på 60W vil lyse sterkest, fordi den har størst motstand'
'40W pæra trenger mindre strøm for å lyse maksimalt'
4.19 Doble strøm og halvere spenning fordi spenning og strøm skal være lik over hver pære.
Første spenning over skyvemotstand. U=RI=5W*100mA=0,5V => 4V over pærene
Ny spenning over skyvemotstanden 4,5V-2V=2,5V
Ny motstand i skyvemotstanden R=U/I=2,5V/200mA=12,5W
4.20 Seriekobling: R=45W+45O=90W
Effekt: P=UI=U²/R=(4,5V)²/90W=0,225W
Paralellkobling: 1/45W+1/45W=1/R => R=22,5W
Effekt: P=UI=U²/R=(4,5V)²/22,5W=0,9W
4.21 Maks strøm ved 0W i skyvemotstand og 21W pære
Min strøm ved 150W i skyvemotstand og 5W pære
R5W=U²/P=(12V)²/5W=28,8W
Minimumstrøm: I=U/R=12V/(150W+28,8W)=0,067A=67mA
4.22 R=U²/P=220V²/40W=1210W
4.23 Hovedlys: R=U/I=U²/P=(6V)²/2W=18W
Bremselys: R=(6V)²/0,6W=60W
Baklys: R=(60V)²/0,4W=90O
4.24 a) U40=220V I40=40W/220V=180mA (R=220V/270mA=1200W)
U60=220V I60=60W/220V=270mA (R=220V/180ma=810W)
b) I40=220V/(1200W+810W)=110mA U40=1200O*110mA=132V
I60=110mA U60=810O*110mA=89V
4.25 a) I=P/U=1W/4,5V=220mA
R=U/I=4,5V/0,22A=20W
b) 1/Rp=1/20W+1/20W => Rp=10W
I=U/R=4,5V/(20+10)W)=150mA i hovedkretsen
I=75mA i en av grenene
U=RI=20W*0,15A=3V over den ene pæra
U=4,5V-3V=1,5V over de to pærene
c) 1->0 => 2 og 3 lyser mer
1->¥
=> 2 og 3 slukner
2->0 => 1 lyser mer, 3 slukner
2->¥
=> 1 lyser mindre, 3 lyser mer (tilsvarende med 3)