C: Universet i rom
C1: Forutsetninger
Etter en kort gjennomgåelse av endel grunnleggende naturlover, vil vi nå se hvordan disse kan hjelpe oss med å forstå universet. Hvordan er det da egentlig mulig for oss jordboere å vite noe om universet der vi aldri har vært? I utgangspunktet er det nok svært lite vi vet. Før vi begynner å studere universet,må vi derfor gjøre en antakelse. Antakelsen er at naturlovene slik vi opplever dem på jorda,gjelder for hele universet (alt rom). Dette synes ganske opplagt for de fleste og vi vil derfor ikke prøve å begrunne det her. Vi vil derimot understreke at denne antakelsen far store konsekvenser for vår utforskning av universet. Det er et faktum at så og si all vår kunnskap om universet har kommet til oss i form av elektromagnetiske bølger (lys, radiobølger, osv.). Vi har her på jorda utforsket sammenhengen mellom materie (masse og ladninger) og stråling. Når vi så antar at naturlovene er de samme over alt i universet, kan vi med en gang si noe om det som har sendt ut de elektromagnetiske bølger som når oss. Når vi ser på ei stjerne er det elektromagnetiske bølger vi ser.
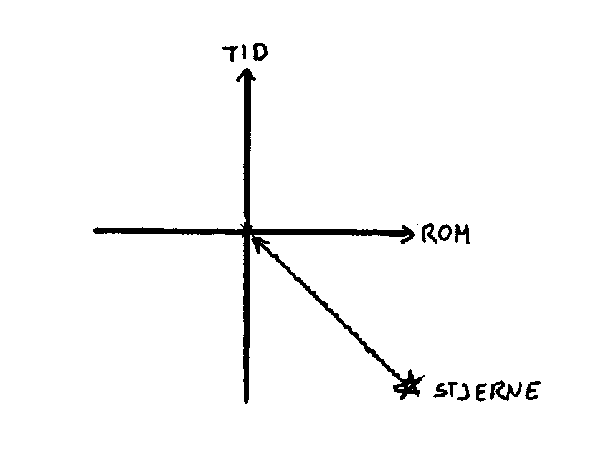
Nå er det en ting til i forbindelse med elektromagnetiske bølger som det er verd å merke seg. Som nevnt tidligere har alle elektromagnetiske bølger ei fast hastighet c. Det betyr at når vi ser utover i rommet ser vi samtidig bakover i tida. Når vi for eksempel ser på den nærmeste stjerna (utenom sola), så ser vi den slik den var for ca. 4 år siden. Dette skyldes at lyset fra stjerna trenger 4 år for å nå oss. Det betyr at i alle praktiske målinger og beregninger av universet må man ta hensyn til både rom og tidsdimensjonen samtidig. Når vi tar for oss romdimensjonen først, så er det utfra et ønske om å gjøre det hele litt enklere.
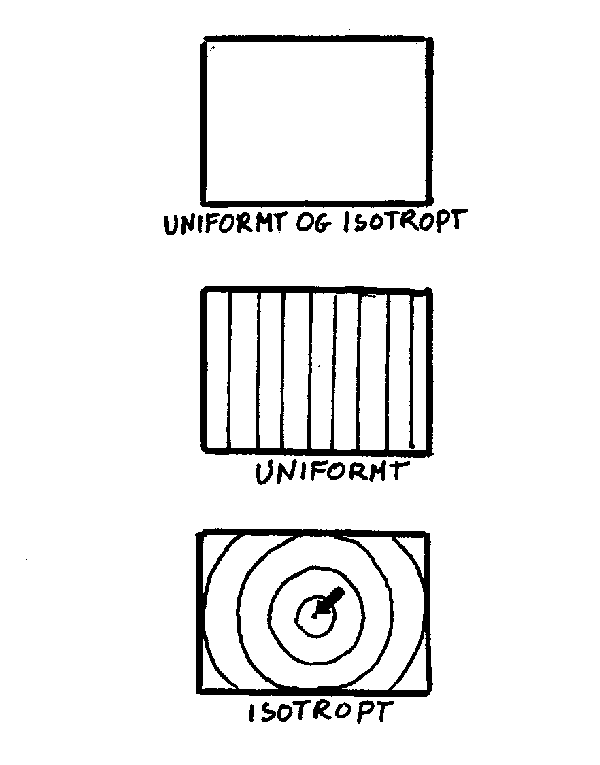
Til slutt i denne innledninga bør det understrekes at når vi snakker om universet som noe kjent, så betyr ikke det at vi kan se hele universet. Dette skyldesf både at nære ting (gass-skyer ol.) skygger for det som ligger lenger borte, og at stjernene synes svakere og svakere jo lenger borte de befinner seg. Alle våre instrumenter (kikkert, radioteleskop ol.) har en begrensning for hvor svake signaler de kan registrere. Dette begrenser også vårt utsyn i universet. Men vi ser ganske mye og det er derfor vanlig på grunnlag av dette å anta at det vi ikke ser er likedan. I denne forbindelsen er det to begreper som er aktuelle. Uniformitet betyr at uansett hvor man er så vil man se noenlunde det samme. Isotropi betyr at uansett hvilken retning man ser i, så vil man se noenlunde det samme. Det betyr med andre ord at det ikke er noen foretrukket retning. For oss på jorda synes det som om universet er tilnærmet uniformt og isotropt, men vi kan aldri være sikker på at dette gjelder hele universet. Mer om dette seinere.
C2: Himmellegemer
Før vi gir en beskrivelse av de forskjellige himmellegemene som finnes, skal vi kort si noe om de sammenhengene som finnes mellom et legeme og den strålingen det sender ut. Alle legemer sender ut stråling. Denne strålinga har sin årsak i at atomene vibrerer eller beveger seg. Dette kalles termiske bevegelser og disse bevegelsene fører til at ladninger akselereres. Vi får da elektromagnetiske bølger . Selve bevegelsene kan man tenke på som en haug med sprettballer i ei eske som ristes. Ballene vil da bevege seg tilfeldig rundt i eska med ulike hastigheter, mens de hele tida støter mot hverandre. Hvis vi så samler opp strålinga fra atomene i slike termiske bevegelser, vil vi få ut elektromagnetiske bølger med forskjellige frekvenser eller bølgelengde. Størst frekvens får vi fra de atomene som har størst termiske bevegelse.
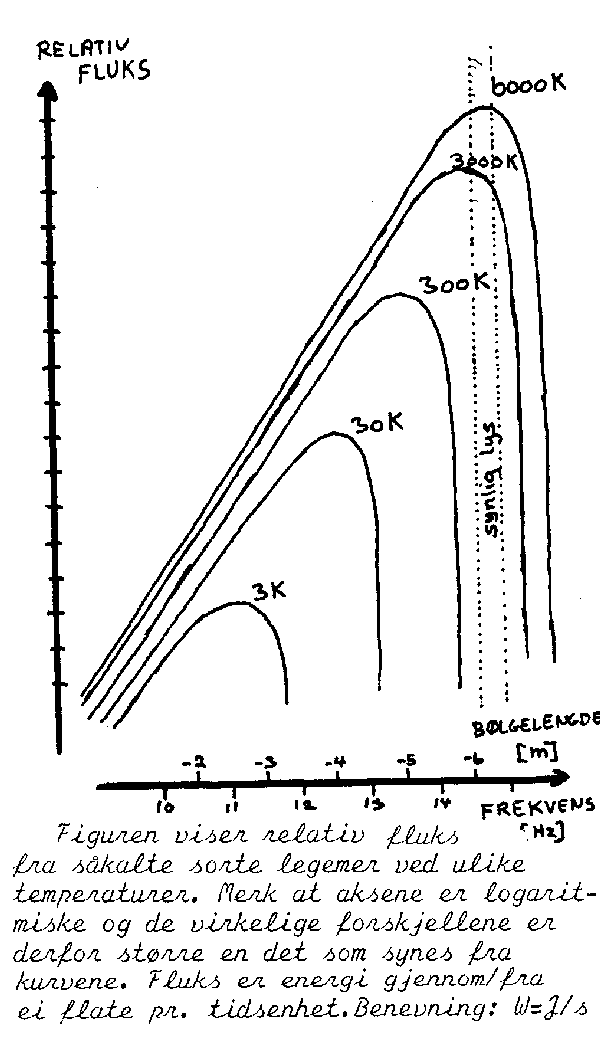
Erfaringer viser at styrken (energien) til de elektromagnetiske bølgene som regel danner et bestemt mønster. Dette mønsteret eller spekteret avhenger av temperaturen på det stoffet som sender ut de elektromagnetiske bølgene. Til høyre vises den relative frekvensfordelinga som et såkalt svart legeme vil sende ut ved ulike temperaturer. Den viser da at de ulike temperaturene gir maksimal stråling ved forskjellige frekvenser, og at den totale utstrålinga øker med temperaturen. Nå har det vist seg at både stjerner og andre legemer stort sett sender ut lys i samsvar med kurvene til venstre, Hvis vi da har spekteret fra ei stjerne, kan dette hjelpe oss med å bestemme stjernens overflatetemperatur.
Merk også at det bare er en liten del av frekvensspekteret som består av synlig lys. Et legeme som bar en temperatur på 300 K vil da ikke sende ut synlig lys. Hvis vi derimot varmer det opp, vil vi se at det begynner å gløde ved en viss temperatur. Det sender da først ut litt rødt lys. Hvis temperaturen øker ytterligere vil fargen bli mer hvit. Nå må det kanskje også nevnes at hvis vi kjøler ned et legeme vil de termiske bevegelsene bli svakere og svakere. Når vi så når -273 °C (0 K) vil de opphøre helt og vi får ingen elektromagnetiske bølger ut. Det er imidlertid vanlig å tro at alt i universet har høyere temperatur en dette absolutte nullpunkt. Det betyr derfor at påstanden om at alle legemer sender ut elektromagnetiske stråler skulle holde.
Når vi så kjenner temperaturen til ei stjerne kan vi beregne hva slags tilstand stoffene i stjerna er i. Med tilstand mener vi her fast stoff, væske eller gass. Nå er alle de synlige stjernene så varme at man regner med at de er i en slags gasstilstand.
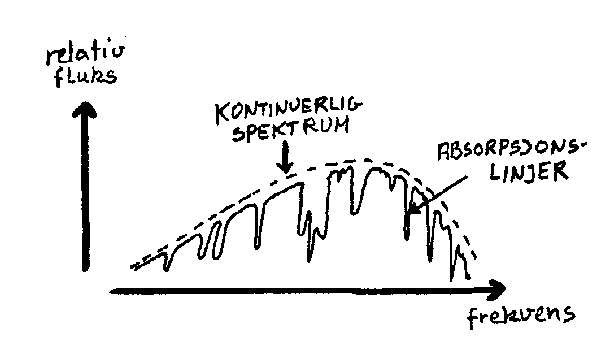
Har vi da noen muligheter for å si noe om hva slags stoffer stjernene består av? Vi vil her kort si litt om hva absorpsjonsspekter og emisjonspekter er. Det viser seg at alle stjerner vil omgi seg med en slags tynnere og kaldere atmosfære som stammer fra stjerna selv. Når lyset går gjennom denne, vil noe av lyset bli absorbert av atomene i denne atmosfæren. Dette medfører at det "oppå" det jevne kontinuerlige spekteret fra stjerna vil bli en mengde såkalte absorbsjonslinjer som skyldes at noe lys er blitt borte. Hvert grunnstoff har sitt karakteristiske absorpsjonsspekter. Dette betyr at vi kan finne ut hvilke stoffer stjerna omgir seg med. Størrelsene på disse absorpsjonslinjene forteller da hvor mye av hvert grunnstoff som finnes i stjerna relativt.
Nå er det riktignok ikke bare omkring stjernene at man får dannet absorpsjonslinjer. Strålingen kan også påvirkes av de stoffene som finnes i rommet mellom stjernene og oss. Det er imidlertid oftest så lite her at man vanligvis ser bort fra dette.
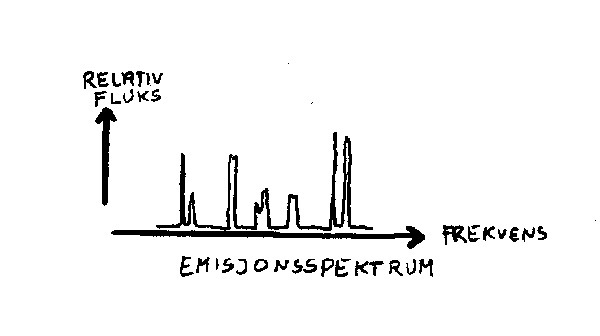
Hvis gass- og støvskyer i universet får tilført energi i en eller annen form vil de sende ut lys med bestemte karakteristiske frekvenser. Vi får da det vi kaller emisjonsspekter og dette kan også fortelle oss litt om hvilke stoffer som finnes i universet.
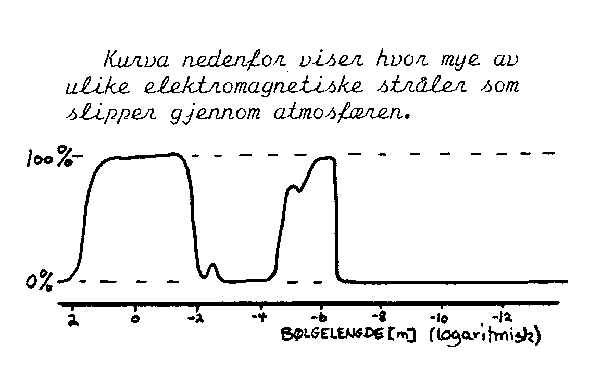
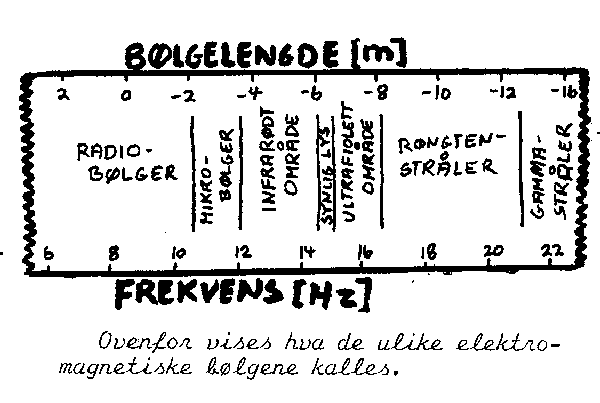
Vi kan imidlertid ikke se bort fra vår egen atmosfære. Den inneholder ulike stoff som vil absorbere stråling med ulike frekvenser. Dette er for eksempel grunnen til at man må sende satellitter i bane utenfor atmosfæren for å måle "den sanne" strålingen som kommer fra universet. Ellers bør vi være glad for at vi har atmosfæren. Mye av strålingen som finnes i universet er farlig for oss og det er atmosfæren som beskytter oss mot den. For å få en oversikt over den elektromagnetiske strålingen som finnes, og hva som slipper ned til oss kan man studere figuren til venstre. Den viser blant annet at atmosfæren stort sett er ganske ugjennomtrengelig. Den slipper imidlertid gjennom synlig lys og endel radiobølger.
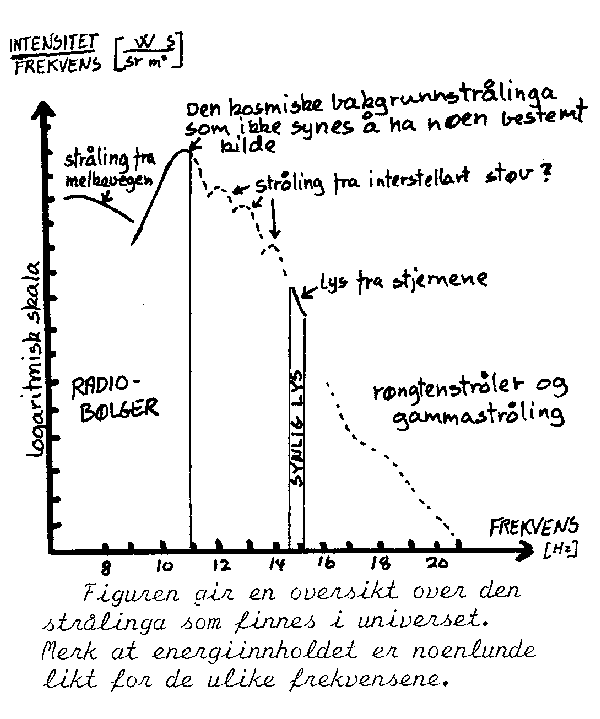
Det er ellers litt interessant å sammenlikne mengden av de ulike strålingstypene som finnes i universet. Dette kan blant annet hjelpe oss med å finne ut hvordan universet har vært i tidligere tider. Figuren til venstre viser hva slags stråling man i gjennomsnitt firmer i universet. Intensitet er her den fluks (energi pr. tid) som kommer fra universet pr. romvinkel og flate. (Benevning:W/sr m2). Dette gir et mål for hvor mye stråling som treffer ei lita flate (m2 ->0 ) fra et lite område på himmelen (sr->0 ). Når vi så dividerer med frekvensen får vi ei kurve som viser gjennomsnittsamplitude eller antall fotoner ved de ulike frekvensene (fig). Lar vi være å dividere med frekvensen får vi ei kurve som viser den relative energifordelingen ved de ulike frekvensene (skisser den). Strålinga som her er kalt kosmisk bakgrunnstråling (3-kelvin-stråling) synes å være helt jevnt fordelt i universet. Det vil si at den er like sterk i alle retninger (isotrop).
Så tilbake til stjernene og det vi vet om dem. Nå er det slik at alle stjerner vi ser vil oppfattes som et punkt uansett hvor sterk kikkert man ser dem gjennom. Vår kjennskap til hvordan gravitasjonskreftene virker, gjør imidlertid at vi regner med at de alle er runde som sola. Egentlig er også sola ei stjerne og mye av våre kunnskaper om andre stjerner har vi fått nettopp ved å studere sola. Den har en form og ulike aktiviteter (solflekker ol.) som vi kan se eller studere direkte ved hjelp av spesielle solkikkerter. Men stjernene varierer både i lysstyrke og lysspekter. Vi skal her kort skissere hvordan man vanligvis klassifiserer eller ordner stjernene i system. Den avgjørende faktoren som gjør at stjernene er forskjellige,er massen av stjernene. Dessuten synes det som om stjernene gjennomgår et livsløp fra "fødsel" til "død" , og utseende av stjerna vi da også være avhengig av hvor langt stjerna er kommet i dette.
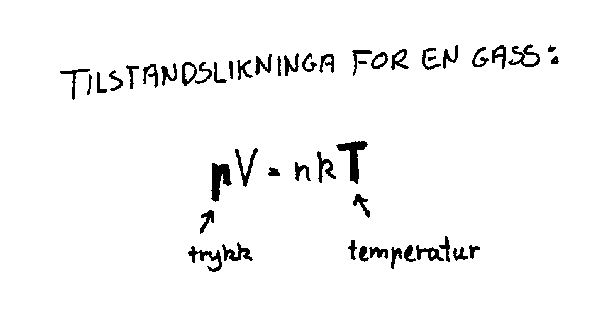
Hvordan avhenger så stjernene av masse og alder? Fra forrige kapittel husker vi at massepartikler tiltrekker hverandre. Dette gjør at atomene i stjerna trekkes sammen. Denne sammentrekkingen vil imidlertid stoppe opp ganske fort. Grunnen er at trykket i stjerna vil øke når den blir mindre. Trykket kan vi da tenke på som en kraft som virker på hvert atom i stjerna, og retningen på denne kraften vil da være motsatt av gravitasjonskraften. Disse kreftene vil da balansere hverandre og vi får en såkalt likevektstilstand. Trykk er da summen av de kreftene som virker når atomer i termiske bevegelser støter mot hverandre. Siden de termiske bevegelsene øker med temperaturen vil også trykket øke med temperaturen. Det betyr kort sagt at hvis temperaturen i ei stjerne øker vil trykket "overstige" gravitasjonskreftene og stjerna vil utvide seg. Hvis derimot temperaturen avtar vil stjerna trekke seg sammen. Merk at stjerner har så høy temperatur at de vil være i en slags gasstilstand og man kan derfor bruke den kjente tilstandslikninga for å beregne ulike forhold i stjerna.
STJERNENES LIVSLØP
Vi vil nå kort beskrive livsløpet til ei stjerne, og så trekke fram forskjellige mulige måter den kan
"ende livet" på. Fordi ei stjerne alltid stråler ut elektromagnetiske bølger vil den hele tida miste energi.
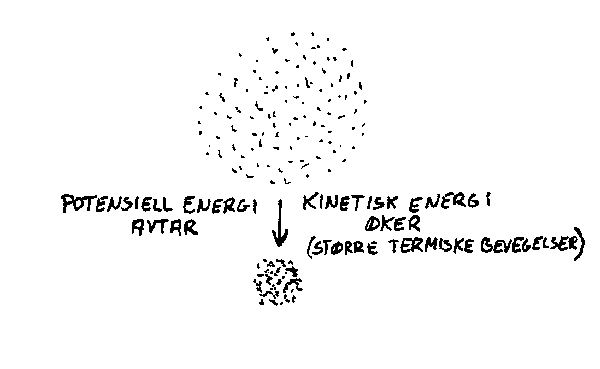
Den vil derfor ubønnhørlig forandres mot en slags slutt-tilstand. Nå kan det diskuteres hvordan stjernene har blitt til, men det er vanlig å anta at de har startet som ei sky av gasser og partikler. Gravitasjonskreftene mellom disse har så trukket dem sammen til en tettere og tettere klump. Nå er det slik at når noe faller i et gravitasjonsfelt
(f.eks. en stein her på jorda), vil den potensielle energien avta. Dette vil også skje i ei "stjernesky" som trekker seg sammen. Den potensielle energien vil da gå over til varme
(kinetisk energi) som gjør at den nydannete stjerna vil oppvarmes. Man
antar da at temperaturen vil i denne prosessen vil kunne øke så mye at kjernereaksjoner
(fusjon) vil kunne starte i sentrum av stjerna. Kjernereaksjonene vil så igjen utvikle varme som vil erstatte den varmen som forsvinner på grunn av stråling fra overflata. Stjerna vil da nå en stabil tilstand som kan vare lenge. Før eller seinere vil imidlertid brennstoffet
(hydrogen) i stjerna ta slutt og resultatet blir da avhengig av massen til stjerna.
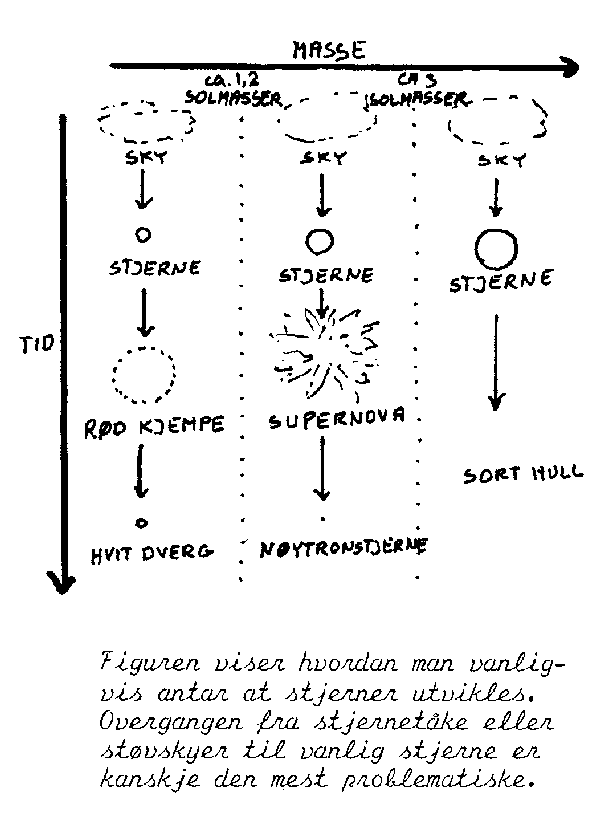
Figuren til venstre viser noen mulige livsløp for ei stjerne.
(1) Hvis massen er liten
(mindre en ca. 1.2
solmasser), vil den indre delen av stjerna trekke seg sammen mens den ytre delen vil
bli presset utover på grunn av en økende stråling innenfra. Det ekspanderende kuleskallet vil så gradvis avkjøles og man får
ei såkalt rød kjempestjerne. Kjernen har da i mellomtida stabilisert seg som en såkalt
hvit dverg. Denne vil så langsomt avkjøles uten at det skjer noen større ytre forandringer.
(2) Hvis massen er litt større, vil den siste sammentrekningen skape en så stor temperatur
og trykkøkning at stjerna vil eksplodere i en enorm supernova. Slike har vært observert
på himmelen fra tid til annen. Noen har også vært så sterke at de har vært synlig til og
med på dagstid. Resultatet av en supernova blir da en svært liten rest med enorm stor
tetthet som kalles nøytromstjerne. Navnet kommer av at vi regner med at elektronene
stort sett er klemt sammen med protonenes og hele stjerna består da bare av en
tett
klump av nøytroner.
(3) Hvis massen av stjerna er enda større, regner man med at gravitasjonskraften vil bli så stor i den siste sammentrekninga at selv ikke de sterke frastøtningskreftene som finnes mellom nøytronene vil klare å motstå gravitasjonskreftene. Dette medfører at nøytronene klapper sammen og etter alt og dømme vil stjerna bli svært liten. Det vil si at tettheten blir svært stor. Dette skaper så store gravitasjonskrefter at selv ikke lyset vil kunne unslippe ifølge Einsteins generelle relativitetsteori. Stjerna er da blitt til et såkalt sort hull.

SORTE HULL
Fordi sorte hull har en spesiell interesse i kosmologien, vil vi kommentere dem litt nærmere her. Ifølge Einsteins generelle relativitetsteori vil rommets rumming her være så stor at tid og rom opphører
(Dt->¥ og Dr -> 0) . På grunn av problemene som er knyttet til dette er det endel som er skeptiske til om sorte hull i det hele tatt eksisterer eller om det er rett å beskrive dem ved hjelp av Einsteins generelle relativitetsteori.
Enkelt kan vi forestille oss hva et sort hull er hvis vi tenker oss at vi beveger oss langsomt mot det. Etterhvert som vi nærmer oss, vil tida gå seinere (Dt blir lengere), og vi vil bli flatere i retningen mot det sorte hullet. Alt dette er sett utenfra, fra en observatør langt borte fra det sorte hullet. Vi som nærmer oss det sorte hullet vil ikke merke noen forskjell bortsett fra en utstrekkingseffekt som skyldes stor variasjon i gravitasjonen. Når vi så når grensa for det sorte hullet (event horizon) vil tida stå stille og rommet vil være helt flatklemt. Ifølge dette skulle det da ikke være mulig å komme lenger. Sett fra jorda opphører rom og tid å eksistere ved kanten av et sort hull. For den som er så uheldig å falle inn i et sort hull vil det hele synes anderledes. Sannsynligvis vil man ikke merke noe (bortsett fra utstrekkingseffekter) før man treffer senteret i det sorte hullet.
Nå er den generelle relativitetsteorien en matematisk beskrivelse av universet og det må advares mot å trekke for raske slutninger utfra beskrivelsen ovenfor. Nå er det imidlertid endel som er skeptiske til om det finnes sorte hull i universet slik som den generelle relativitetsteorien forutsier. Ei innvending er nettopp det at det er problematisk å forestille seg et sted i rommet hvor krumminga er så sterk at rom og tid på en måte opphører. Ingenting kan heller nå ut til oss fra et sort hull og Einsteins beskrivelse av et sort hull kan derfor heller ikke testes på vanlig mate.

Nå kan man fra tid til annen lese ulike teorier om hva som er inni et sort hull. Enkelte har forestilt seg at krumminga rundt et sort hull fortsetter på baksida i et annet univers (se figuren). Det er ikke noe i vegen for å filosofere over dette, men det kan neppe kalles vitenskap da vitenskapen slik vi vanligvis tenker på den handler om det som er i rom og tid.
Til slutt i dette avsnittet om himmellegemer, vil vi også nevne at det finnes store gass og støvkonsentrasjoner i universet som vi kan observere fordi de skygger for bakenfor liggende stjerner eller fordi de sender ut stråling. Dessuten vet vi at vår sol er omgitt av planeter, og det er derfor ikke unaturlig at det også finnes planeter andre steder i universet. Disse vil imidlertid være så små at vi ikke kan regne med å observere dem direkte.
Vi har nå kort sett på den materien som finnes i universet. Nå er det imidlertid viktig å være klar over at dette utgjør en svært liten del av universet. Mesteparten av universet består av tomt rom og ulike elektrcmagnetiske bølger.
C3: Avstander og plassering
Vi har nå gitt en kort oversikt over hva vi finner i universet. Neste tema blir da å prøve å danne seg et bilde av hvor dette er. Det betyr i hovedsak hvordan stjernene er fordelt utover i universet. Først litt om hvordan man beregner avstander til de forskjellige himmellegemene. Å bruke et meter mål er opplagt ikke noen god metode. Denne metoden forutsetter for eksempel at man kan bevege seg mellom punktene man skal måle avstanden mellom. Vi skal her bare kort skissere de viktigste metodene for å måle avstander i rommet.
(l) De nærmeste himmellegemene (månen ol.) kan man måle avstanden til ved hjelp av radiosignaler. Man beregner da avstanden utfra hvor lang tid et signal bruker fra jorda og til det er blitt reflektert tilbake til jorda.
(2) I solsystemet vårt vil også Newtons lover være til, hjelp da de forteller om sammenhenger mellom for eksempel omløpstid rundt sola og planetenes avstand fra sola (Keplers 3. lov).
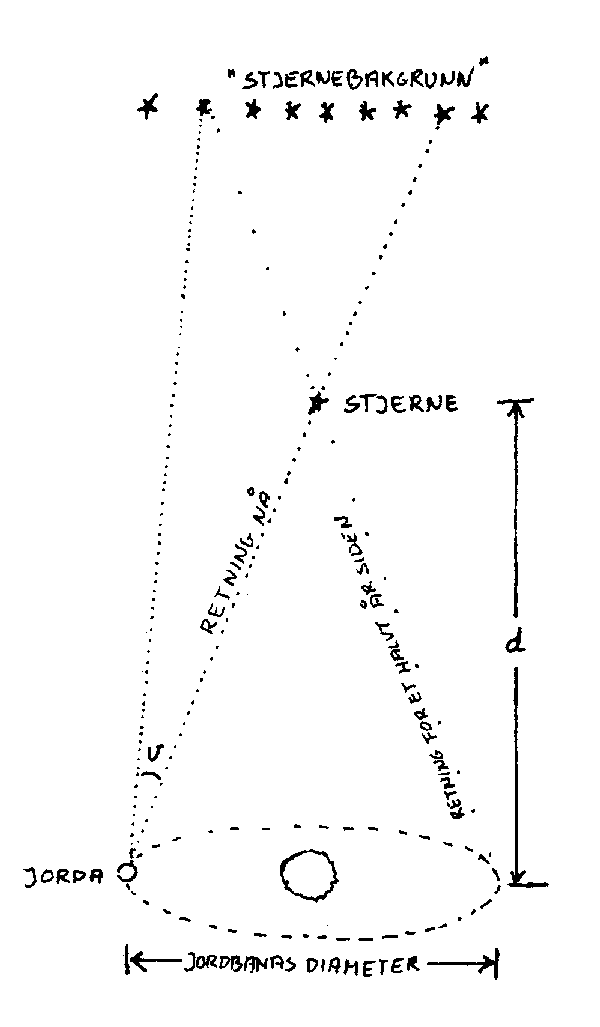
(3) Når det gjelder de nærmeste stjernene er den såkalte parallaks-metoden vanlig. Den gjør bruk av det faktum at noen stjerner synes å flytte litt på seg når jorda gar rundt sola. I prinsippet er det det samme som skjer når for eksempel et tre forflytter seg i forhold til horisonten når vi beveger oss litt. Hvis vi måler den vinkelen som ei stjerne har flyttet seg i løpet av et halvt år (v), så kan vi beregne avstanden til stjerna (d) når vi på forhånd kjenner diameteren til jordbana. Denne metoden er ikke brukbar så langt utover i universet. Den har imidlertid vært nyttig for å bekrefte Hertzsprung-Russel-diagrammet som er grunnlaget for den neste metoden.
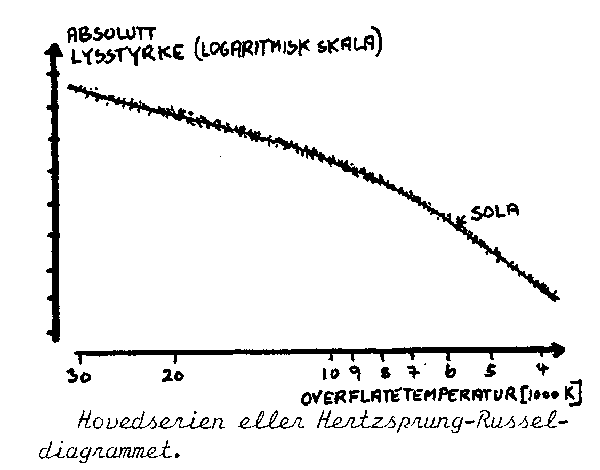

(4) Hertzsprung-Russel-diagrammet (til venstre) forteller kort og godt at det er en sammenheng mellom overflatetemperaturen (eller fargen) til ei stjerne og den absolutte lysstyrke til stjerna. Med absolutt lysstyrke mener vi her den lysstyrken man ville observert fra stjerna hvis man var plassert i en bestemt avstand fra den (10 pc. eller ca 33 lysår). Vi kan finne overflatetemperaturen ved hjelp av stjernespekteret. Diagrammet til venstre viset da hvilken absolutt lysstyrke stjerna sender ut, og ved å sammen likne denne med den lysstyrken vi observerer her på jorda (tilsynelatende lysstyrke) kan man så beregne avstanden til stjerna. Uten at vi skal gå noe mer inn på hvordan man kan beregne avstander ved hjelp av lysstyrker så vil vi bare nevne at lystyrken rundt ei lyskilde varierer som 1/d2 hvor d er avstanden til lyskilden.
(5) Nå finnes det også spesielle variable stjerner som har en kjent sammenheng mellom absolutt lysstyrke og variasjonsfrekvensen (Cepheider). Disse stjernene vil altså ved hjelp av blinking fortelle hva den absolutte lysstyrken er. Dette gjør da at vi kan beregne avstanden til dem.
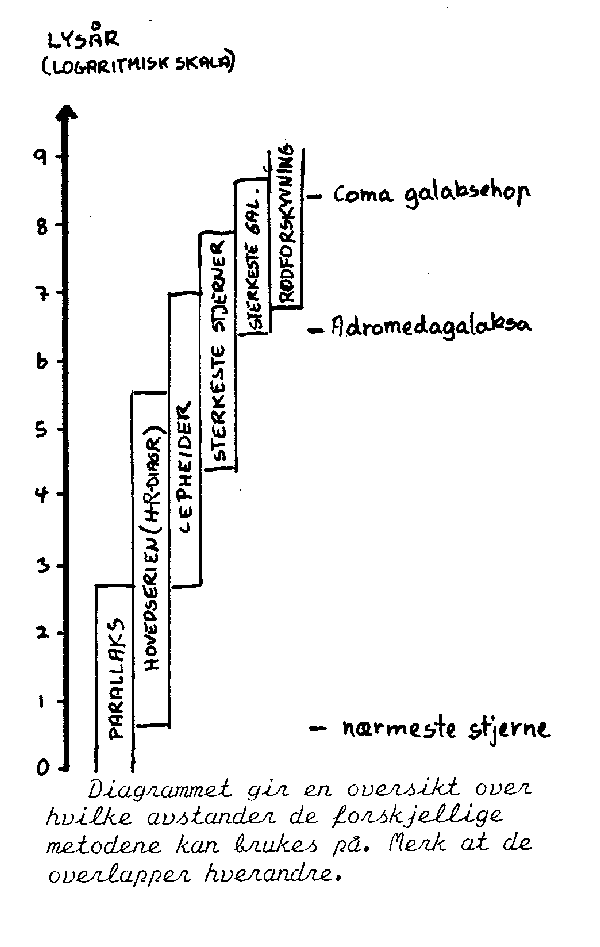

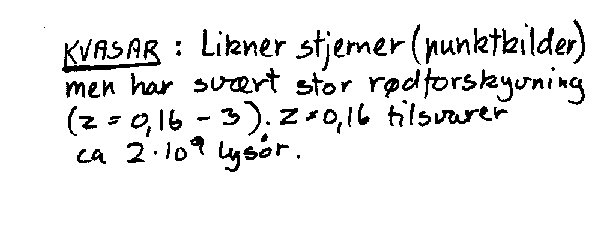
(6) Nå er det imidlertid grenser for hvor langt utover i universet vi kan se disse stjernene. En metode som er brukbar litt lenger, følger av at vi antar at de mest lyssterke stjernene i hver galakse eller stjernehop er omtrent like sterke. Det vil si at vi antar at de har lik absolutt lysstyrke.
(7) Når vi så ikke lenger kan skille de forskjellige stjernene fra hverandre kan vi i stedet sammenlikne lysstyrken til de mest lyssterke galaksene i hver av galaksehopene. Dette gir oss så en måte til å bestemme avstanden til endel galaksehoper.
(8) Nå er vi imidlertid kommet så langt ut i universet at den såkalte rødforskyvningen gjør seg gjeldene. Rødforskyvning betyr kort at kjente absorpsjonslinjene i lyset fra fjerne himmellegemer befinner seg litt lenger mot den røde sida av spekteret enn de burde. Det synes som om denne rødforskyvninga øker med avstanden,og avstanden til de fjerneste himmellegemene bestemmes da ved hjelp av rødforskyvning. Mer om rødforskyvning seinere.
Mens vi er inne på avstandsmålinger vil vi kort nevne at vi mottar radiobølger fra tilsynelatende usynlige radiokilder. Problemet her er at vi foreløpig ikke kjenner noen metoder å beregne avstanden til disse på. Vanligvis blir det antatt at de er svært langt borte.
Et annet problem for de som skal avgjøre avstander til fjerne himmellegemer er de såkalte kvasarene. De har svært stor rødforskyvning og skulle følgelig være svært langt borte. Men fordi de også har forholdsvis stor tilsynelatende lysstyrke, må den absolutte lysstyrken da være enorm. Problemet er da om denne enorme energiutviklinga som kvasarene synes å ha egentlig er fysisk mulig. Forskerne har foreslått ulike prosesser for å forklare dette, men foreløpig er det ingen som er allment akseptert. Noen har også antatt at kvasarene ikke er så fjerne som rødforskyvninga skulle tilsi. De unngår da problemet med å forklare årsaken til en enorm energiutvikling, men får i stedet problemer med å forklare årsaken til den store rødforskyvninga. Her vil vi bare nevne at de fleste vel antar at kvasarene er fjerne himmellegemer som muligens er galaker på et tidlig stadium av utviklinga. Husk at når vi ser ut i rommet ser vi samtidig bakover i tida.

>BEVEGELSER. Nå er det viktig å være klar over at universet ikke er statisk eller stillestående. Alt synes å bevege seg mer eller mindre i forhold til hverandre. Disse bevegelsene kan vi dels observere direkte ved at enkelte stjerner beveger seg over himmelen. Denne bevegelsen er imidlertid så langsom at man trenger endel år for å observere den. Dernest kan vi observere bevegelser i universet ved at spekteret fra stjernene er en tanke rød- eller blåforskjøvet (Doppler-effekt). Vi skal komme tilbake til Doppler-effekten seinere, men her vil vi bare si at den forteller om stjernene beveger seg fra eller mot ors. Det er også endel ting i universet som indirekte vitner om bevegelser. Et eksempel er formen på spiralgalaksene. Disse synes å ha fått sin nåværende form som en følge av rotasjon, og det er ingen grunn til å tro at de plutselig har stoppet opp (jfr. Newtons lover).
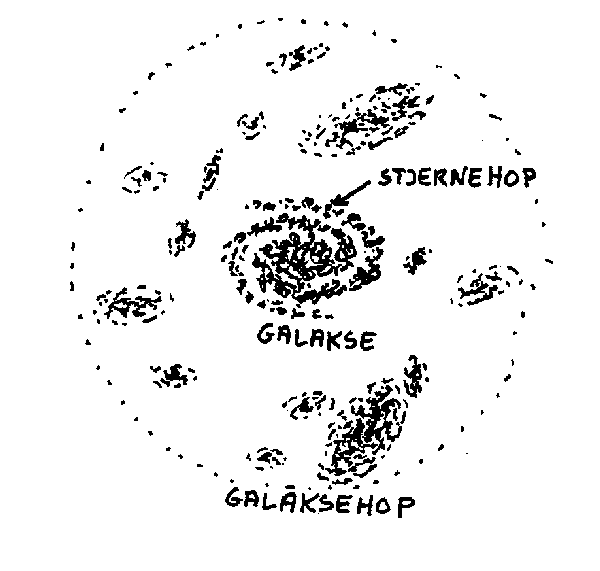
Til slutt i dette avsnittet on himmellegemenes plassering vil vi nevne at stjernene synes å være samlet i såkalte stjernehoper. I var galakse kan det være i størrelseorden 15 000 slike. Mer kjent er nok imidlertid de såkalte galaksene. Disse kan ha mer eller mindre karakteristiske former. Mest kjent er nok de såkalte spiralgalaksene. Vår egen galakse, Melkevegen, er en spiralgalakse med omkring 2•l011 stjerner. Galaksene synes videre å være samlet i såkalte galaksehoper. Disse inneholder så noen hundre galakser.

Nå er det begrenset hvor mange galaksehoper vi kan observere fra jorda, og det er derfor litt usikkert hvordan disse er plassert utover i universet. De fleste observasjonene tyder imidlertid på at de er plassert noenlunde jevnt utover i den synlige delen av universet. Det betyr med andre ord at den synlige delen av universet er tilnærmet uniformt og isotropt når det gjelder plassering av galaksehoper. Nå hender det fra tid til annen at noen mener å ha observert unntak fra denne regelen. Vi vil imidlertid antes at den synlige delen av universet er uniform og isotrop. Dessuten vil vi antes at dette også gjelder den delen av universet som vi ikke kan se. Grunnen er at dette er nødvendig antakelse i kosmologien. Hvis ikke dette er tilfelle kan vi strengt tatt ikke si noe om universet som helhet. Alt kan på en måte være mulig. Nå kan det være verd å merke seg at de kosmologiske modellene som vi skal presentere seinere er avhengige av at antakelsen ovenfor gjelder.
C4 Universet i en boks
Vi skal nå ved hjelp av en enkel og elegant metode prøve å lage oss et bilde av hvordan universet som helhet er oppbygd. Metoden er avhengig av at universet er isotropt og uniformt. Prinsippet er kort og godt at vi tenker oss at vi tar et utsnitt av universet, og så studerer vi dette. Deretter ekstrapolerer vi resultatet til å gjelde hele universes.
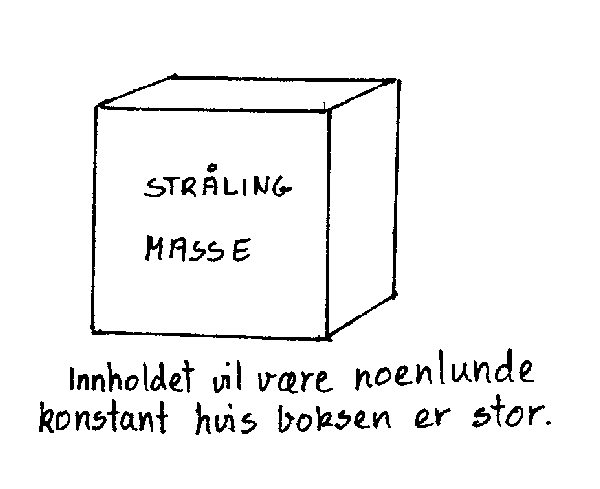
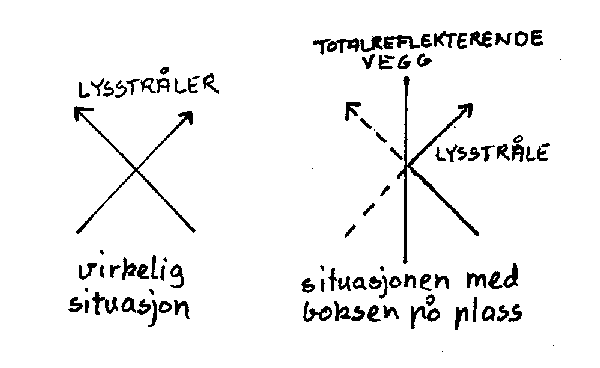
Merk først at vi kan betrakte universet som noe som inneholder stråling og masse. Hvis vi så ser stort på det, kan vi si at både stråling og masse er jevnt fordelt i universet. Dessuten kan vi også si at de bevegelsene som finnes i universet i gjennomsnitt vil være lik i alle retninger. Det betyr at hvis vi tenker oss et avgrenset rom i universet, vil innholdet av dette være noenlunde konstant fordi det som eventuelt forsvinner ut vil oppheves av det som kommer inn. Vi tenker oss så at vi plasserer en masseløs og totalreflekterende vegg rundt rommet vårt. Vi får da et såkalt lukket system hvor inn holdet i boksen ikke vil ha noen kontakt med det som er utenfor. Merk at strålingen og massefordelingen i boksen ikke i vil forandres som følge av dette. Istedet for at en utgående lysstråle erstattes av en inngående lysstråle vil lysstrålene i boksen reflekteres fra veggen. Umiddelbart vil man vel tenke at gravitasjonskreftene virker gjennom veggen og forstyrrer isolasjonen. Nå er det imidlertid slik at gravitasjonskreftene i et uniformt og isotropt univers vil oppheve hverandre slik at vi bare kan to hensyn til den massen som er inni boksen. Det betyr at vi kan begrense vårt studium av universet tit en avgrenset boks, og da nyte godt av alle de forenklinger som gjelder når vi har med et lukket system å gjøre.

Merk at boksen også kan representere et univers som utvider seg eller trekker seg sammen. I disse tilfellene må imidlertid veggene flyttes sammen med gjennomsnitts-strømmen slik at summen av inngående og utgående strøm vil bli lik null. En utvidelse av universet kan oppfattes på to måter. Enten betyr det at selve rommet utvider seg, eller så betyr det at utvidelsen foregår i rommet. I første tilfellet får vi problemer med å definere hva utvidelsen foregår i forhold til. I andre tillfellet får vi problemer med å klargjøre forskjellen på rom og univers. Vi skal komme tilbake til dette seinere.
Så skal vi se hvordan denne boksen kan hjelpe oss med å forstå de ulike kosmologiske modellene som følger av Einsteins generelle relativitetsteori. Nå er det imidlertid slik at Newtons mekanikk gir samme resultat som Einsteins generelle relativitetsteori i dette tilfellet, og da den er mye lettere å forstå vil vi bruke den her. Fra den generelle relativitetsteorien henter vi da bare antakelsen om at massen krummer rommet. Siden boksen vår bare representerer et mindre utsnitt av universet kan vi se bort fra krumminga foreløpig.
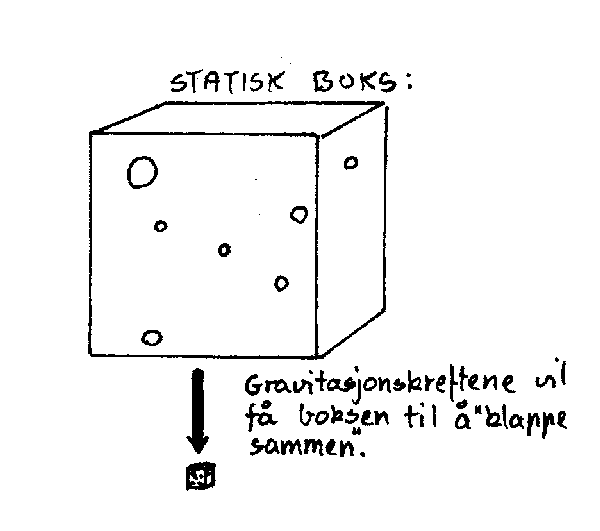
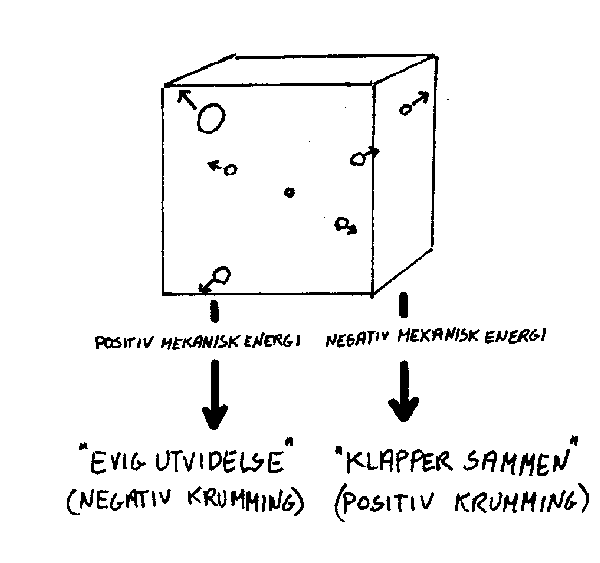
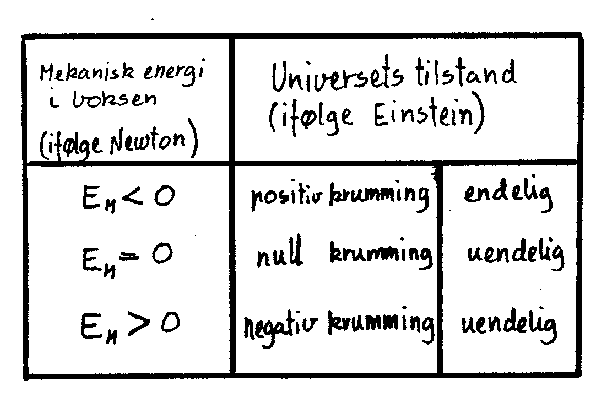
Vi tenker oss først at massen som er i boksen i form av stjerner og liknende er i ro. Hva vil da skje? Jo, gravitasjonskreftene vil virke mellom de ulike massene og de vil begynne å bevege seg mot et felles tyngdepunkt midt i boksen. Energien vil da hele tida være bevart slik at potensiell energi vil gå over til kinetisk energi. Veggene vil i dette tilfellet følge med, og det hele vil ende med at alt klapper sammen. Dette gjorde at Einstein i si tid antok at det fantes en slags kosmologisk kraft som motvirket dette. Han antok da altså først at universet var statisk og at det ble holdt utstrekt av en kosmologisk kraft. Nå oppdaget man imidlertid seinere den såkalte rødforskyvninga fra de fjerneste galaksene.og denne ble da tolket som Doppler-effekt. Det betydde i så fall at universet utvidet seg og den kosmologiske kraften ble da overflødig. For vår boks betyr det at massene inni boksen beveger seg fra hverandre og at boksen utvider seg. Hva kan da skje? Avhengig av om den mekaniske energien er positiv eller negativ (), vil boksen vår fortsette å utvide seg for alltid eller så vil den før eller seinere begynne å trekke seg sammen igjen. Dette følger av Newtons mekanikk. Ifølge Einsteins relativitetsteori tilsvarer dette at universet har negativ eller posi.tiv krumming. Er den mekaniske energien null vil også krumminga være null. Se skjemaet under.
Hvis vi så tenker på universet som helhet, vil positiv krumming tilsvare at universet bare vil utvide seg ei stund. Deretter vil det begynne å trekke seg sammen igjen. Størrelsen av universet blir da endelig. Hvis krumminga er lik null vil universet utvide seg for alltid, og universet er da også uendelig stort. Dette gjelder også hvis krumminga er negativ. Hva universets virkelige krumming er skal vi komme tilbake til seinere. Det er nemlig mulig å beregne den mekaniske energien i universet ved å studere fjernt liggende galakser. Prinsippet er at man beregner den totale massen i en tilfeldig stor "boks" og så finner man avstand, masse og hastighet til galakser ved kanten av boksen. Man kan da finne den mekaniske energien til disse galaksene. Hvis universet er homogent og isotropt vil alle galaksene i en slik tilfeldig boks ha samme mekaniske energi når krumminga er null. Hvis Einsteins teori er rett vil da disse beregningene vise om universet har positiv eller negativ krumming. I praksis bruker man som regel kuleformede "bokser", men prinsippet er det samme som antydet her.

C5: Termodynamikk
Fordi termodynamikkens lover også er nyttige når vi studerer universet, vil vi kort si noe om dem her. Den første hovedsetninga sier blant annet at energien i et lukket system er konstant. Det betyr at den energien vi har inni boksen vår vil holde seg konstant uansett om den utvider seg eller trekker seg sammen. Nå oppstår det imidlertid et problem når vi ser på totalenergien i en boks (et univers) som utvider seg. Når ei lysstråle treffer et speil vil det vanligvis sendes uforandret tilbake.
Det kan imidlertid vises at hvis speilet beveger seg bort fra observatøren, vil den reflekterte lysstrålen ha litt lengere bølgelengde når den når tilbake til observatøren (lyset er rødforskjøvet). Hva skjer så i et univers som utvider seg? "Boksmetoden" som er beskrevet foran forutsier da at et foton som treffer en vegg i en boks som utvider seg, vil bli rødforskjøvet. Dette gjelder både hvis man betrakter utvidelsen som en utvidelse i rommet og en utvidelse av rommet. Dette betyr igjen at hvert foton får mindre energi når universet, eller boksen vår utvider seg. Det er for eksempel vanlig å betrakte den såkalte bakgrunnstrålinga eller 3-kelvin-strålinga som et resultat av at mer energirike fotoner er blitt "dradd ut" fordi universet har utvidet seg.

Problemet er imidlertid at det samlete antall fotoner i universet (eller boksen) vil være konstant hvis vi ser bort fra de som absorberes og emitteres ifra materien. Når så hvert foton mister energi vil totalenergien i universet avta når universet utvider seg. Man har med andre ord fått en konflikt mellom to grunnleggende antakelser i fysikken (energibevarelsen) og universet (et lukket system) og ideen om at universet utvider seg.
Hvordan"løses" så dette problemet? I tilsvarende problem i termodynamikken vil den "tapte" energien overføres til veggene i den aktuelle boksen som utvider seg. Veggene i vår "univers-boks" er ikke virkelige vegger som kan motta energi, og det er derfor nødvendig å finne andre løsninger. Mange bøker om kosmologi tar ikke opp dette problemet og har følgelig heller ikke noen løsning på det. I bøker som tar opp problemet er det vanlig å anta at energibevarelsen ikke gjelder for universet som helhet*
*COSMOLOGY p276: ... If
the universe possessed a cosmic edge, the situation would be different; the pressure at
the edge could then do work, and we would have a universe similar to a steam engine.
But the universe has no edge, and the pressure everywhere is therefore impotent and
unable to produce mechanical energy. The conclusion, whether we like it or not, is
obvious: Energy in the universe is not conserved.....
universe. To the questions where the energy goes in an expanding universe and where it comes in a collapsing universe the answer is - nowhere, because in this one case energy is not conserved.
Problemet med dette er vel særlig at energibevarelsen er en av de grunnleggende lovene i fysikken. En annen løsning er at universet ikke utvider seg. Mer om dette seinere.

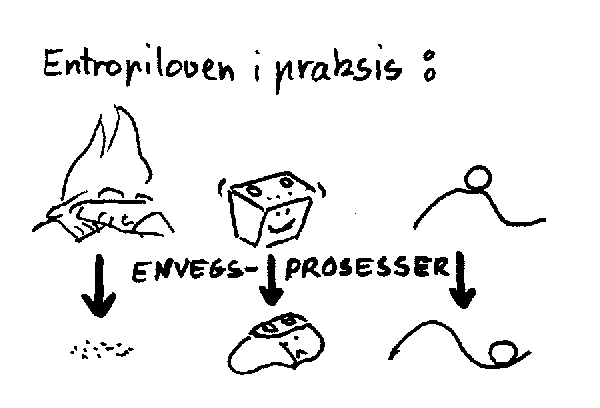
TERMODYNAMIKKENS 2. HOVEDSETNING.
Denne kan også illustreres ved hjelp av boksen vår.
På en enkel måte kan vi få fram det sentrale i denne setninga ved å tenke oss en todelt boks.
Vi antar så at temperaturen er litt forskjellig i de to delene (T1> T2 ). Den andre hovedsetninga
sier da at det vil strømme energi fra den varme til den kalde delen,
ikke omvendt. Det betyr at entropien(S) vil øke. Entropien
blir da på en måte et mål for graden av uorden i boksen. Høy entropi tilsvarer mye
uorden. Nå er det vanskelig utfra dette å forstå fullt ut hva denne 2.hovedsetninga sier.
Vi vil her kort se på noen eksempler.
Det kan være nyttig å tenke på den 2.hovedsetningen (entropiloven) som noe som forteller om enveisprosesser i naturen. Endel forandringer i naturen går altså bare en veg. Prinsippielt kan man tenke seg at de kunne gå motsatt veg, men sannsynligheten for dette er så liten at vi i praksis regner det som umulig. Ved brenner til aske, batteries utlades, steiner faller ned fjellsider,osv. er alle eksempler på naturens envegsprosesser. Nå må det her tilføyes at vi kan gripe inn og lokalt snu enkelte prosesser, men det er bare på bekostning av en økning i entropien på et mer globalt plan. Loven gjelder altså bare for et lukket system, og universet blir vanligvis regnet som et slikt.
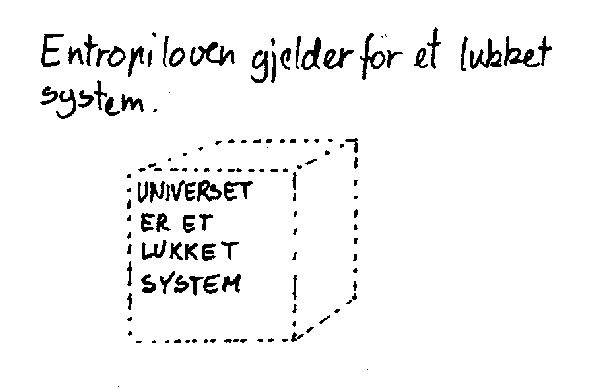
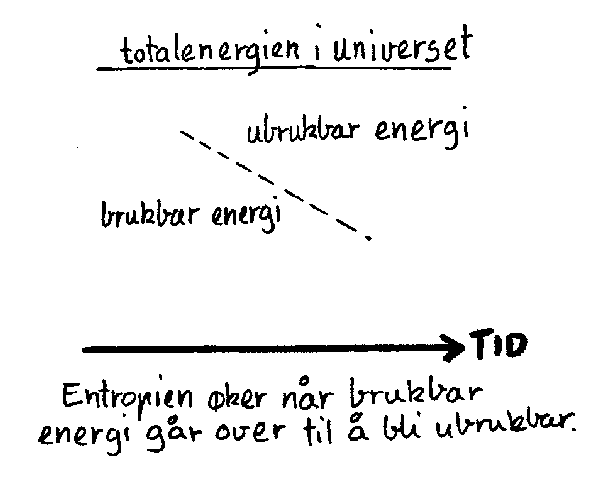
Så tilbake til boksen vår. Stjernene er varmere enn omgivelsene. Det medfører at energi overføres fra stjernene til omgivelsene og entropien øker. Resultatet på lang sikt blir da at både stjerner og omgivelser vil ende på samme temperatur. Da vil alt stoppe opp fordi det ikke lenger vil være noen temperaturforskjeller som kan brukes til å gjøre arbeid. Uten at vi skal gå noe videre inn på det vil vi bare nevne at bilmotoren er et eksempel på at temperaturforskjeller brukes til å gjøre et arbeid. Nå vil nok noen innvende at det også finnes andre energikilder som kan brukes for å utføre arbeid. Eksempler er gravitasjonsenergi, elektrisk energi, atomenergi ol. Poenget her er imidlertid at også disse er underlagt entropiloven. Det betyr i praksis at på langt sikt vil alle gravitasjonspotensial og elektriske potensial være "oppbrukt" fordi hele naturen gradvis går mot en størst mulig grad av uorden eller entropi. Totalt sett kan vi derfor si at selv om energien i universet er konstant vil den delen av energien som an brukes til arbeid, stadig avta.

I var boks vil altså entropien alltid øke. Dette vil i et lukket univers tilsvare at all masse og stråling før eller siden vil tørne sammen i et tett og homogent område hvor alle temperaturforskjeller er utjevnet. Situasjonen blir da at ingen steder i denne lille "miniboksen" vil skille seg fra andre steder og det vil derfor ikke kunne bli utført arbeid i vanlig forstand. Det som kjennetegner et univers med maksimal entropi er at alt (stråling og masse) er helt jevnt fordelt i en slags tilfeldig homogen suppe. Hvis universet er åpent, og følgelig vil ekspandere i all fremtid, vil temperaturen synke mot det absolutte nullpunkt. All masse vil da være spredt utover så langt at all gjenforening ved hjelp av gravitasjonskrefter ville være umulig.
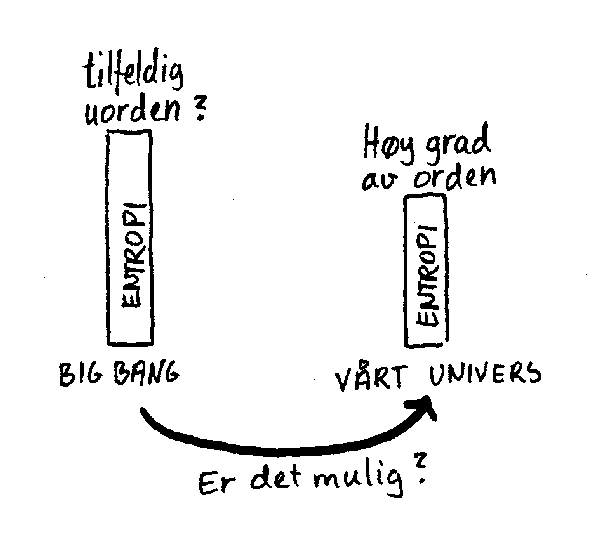
Nå er det særlig når vi tenker bakover i tida at entropibegrepet skaper endel problemer i kosmologien. I dag er det mange som antar at universet begynte med et såkalt Big Bang hvor den første fasen var svære tett. Når man regner på forholdene i denne første tette perioden av universets historie, antar man oftest at universet var tilnærmet homogent på mikro- og makronivå. Dette gjør alle beregninger mye enklere. Hvis dette er tilfelle skulle det bety at entropien var ganske høy. I dag derimot snakker man ofte om et ganske ordnet univers med en forholdsvis lav grad av entropi. Ordet kosmos er for eksempel det motsatte av kaos og gjenspeiler at universet har en forholdsvis høy grad av order.
Hvis dette er tilfelle betyr det at entropien har avtatt fra universets første tette fase og fram til i dag. Dette er imot entropiloven og det skaper derfor endel hodebry for forskerne. På grunn av disse problemene er det derfor endel som antar at universet helt fra første stund har hatt en form for order selv om de foreløpig har litt problemer med å beskrive hvordan den har fungert. Andre mener at det finnes noen hittil ukjente ordningsprinsipper i naturen som på ulike måter kan oppheve entropiloven.
C6: Universets ende
Til slutt i dette kapittelet skal vi se litt på noen argumenter som er knyttet til om universet har grenser eller ikke. Først et prinsipp som er grunnleggende for kosmologien.
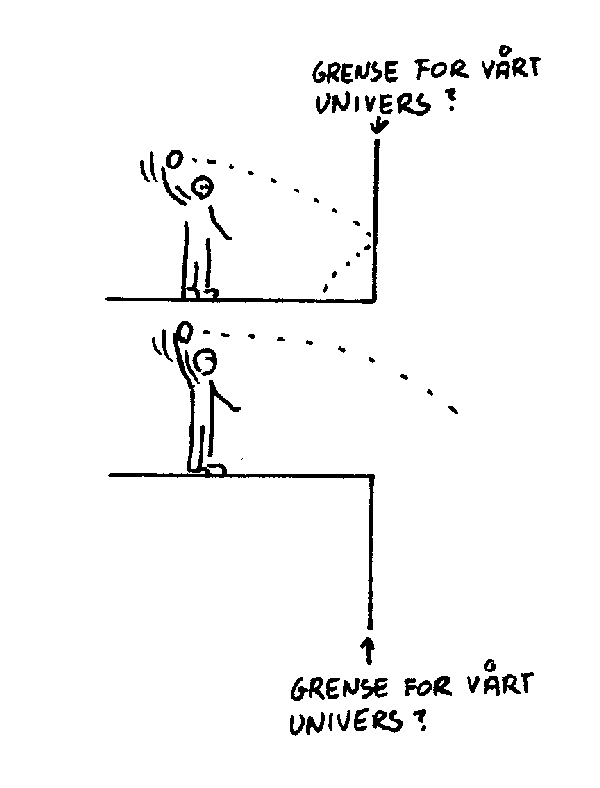
Innholdsprinsippet (containment principle): "Det fysiske universet inneholder alt som er fysisk og ingenting annet." Det betyr for eksempel at begreper som himmel, Gud ol, må underlegges fysiske lover og begrensninger hvis de skal finnes i universet. Mange mener derfor at disse finnes utenfor vårt fysiske univers (Gud er overnaturlig). Men hvor kan så det være? Nå kan man prinsipielt tenke seg at det finnes et eller annet sted utenfor vårt univers som også består av rom og tid. Dette innebærer imidlertid at det finnes ei grense et eller annet sted som markerer slutten på vårt univers. Vi vil kort se på noen problemer som ei slik grense skaper.
Tenk deg at du står ved grensa av vårt univers. Tenk deg så at du kaster en stein mot kanten. Hva skjer? Enten vil da steinen bli kastet tilbake fra denne grensa fordi den er stoppet av noe fysisk. Men det betyr at det finnes noe fysisk utenfor universets grense og det er da tvilsomt om man kan kalle dette universet grense. En annen mulighet er at steinen fortsetter forbi universets grense. Men dette betyr jo at steinen som jo er fysisk, befinner seg utenfor universet. Også dette skaper problemer i forhold til prinsippet ovenfor. Det er derfor vanlig å anta at universet ikke har en slik grense som er beskrevet ovenfor. Det betyr i praksis at universet enten er uendelig stort eller at det har positiv krumming.
Nå er det noen som tenker som så at alt som er, er fysisk. Dette innebærer at Gud ikke kan eksistere hvis vi ikke kan finne ham i vår fysiske verden. Dette er imidlertid en litt tvilsom argumentasjon. De fleste som tror på en Gud tenker seg at han er overnaturlig eller i en slags fjerde dimensjon. Her er vi inne på en annen type grense som finnes i universet. Liksom et vesen på ei todimensjonal kuleflate sett fra vårt tredimensjonale synspunkt, opplagt har et tredimensjonalt rom som nærmeste nabo, kan vi tenke oss at vi har et firedimensjonalt "overrom" som nærmeste nabo. Vi vil imidlertid ikke ha noen muligheter for å se inn i dette fordi vi er begrenset av våre tre dimensjoner. Derimot er det mulig å tenke seg at et vesen fra "overrommet" kan se oss. I de fleste religionene tenker man seg at Gud befinner seg i ei åndelig virkelighet som kan sammenliknes med det "overrommet" vi har antydet ovenfor. Siden det ikke finnes noen vitenskapelige metoder til å kontrollere om dette virkelig finnes skal vi ikke diskutere dette noe mer her.
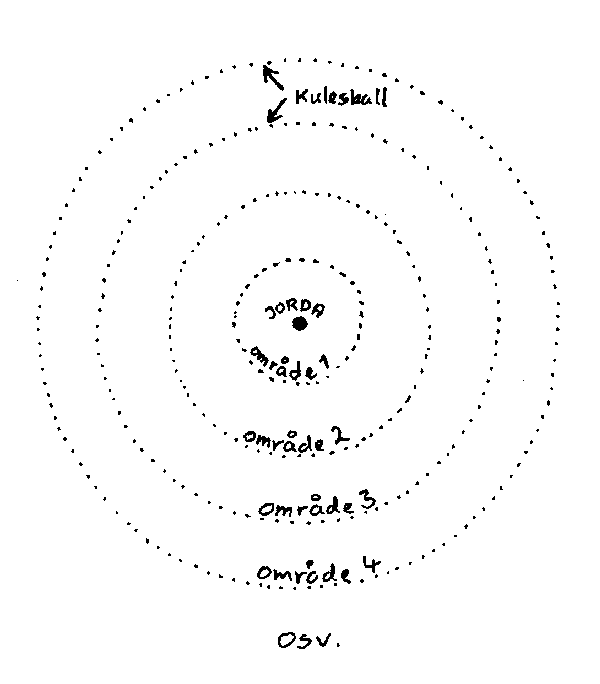
OLBERS PARADOKS.
Er så universet endelig eller uendelig stort? Helt siden Keplers tid har
det såkalte Olbers paradoks vært fremsatt som et argument mot at universet er uendelig
stort. Resonnementet er som følger: Tenk deg området rundt jorda oppdelt i flere
like tykke områder adskilt av kuleskall. Se figuren til venstre. Da vil vi motta like mye
lys fra hvert av disse områdene hvis universet er uniformt. Grunnen er at hvis
vi ser utover i universet vil lyset fra stjernene avta som 1/r2 hvor r er avstanden
til stjernene. Samtidig vil imidlertid antall stjerner øke som r fordi volumet av hvert
område øker utover. Nå vil nok nære stjerner skygge litt for fjernere stjerner, og stjerne
tåker og støvpartikler vil absorbere litt fra de fjerneste områdene. Men på lang sikt
vil det støvet som absorberer lys selv bli oppvarmet slik at det sender ut lys.
Resultatet skulle da være at uendelig mange områder utover totalt sett skulle sende ut så
lys at nattehimmelen skulle synes lys og ikke mørk slik vi ser den.
Noen har så trukket den slutningen at universet da ikke kan være uendelig stort. Senere da man oppdaget rødforskyvningen fra de fjerneste galaksene brukte man dette til å begrunne hvorfor natt-himmelen ikke var lys. Lyset fra de fjerneste områdene skulle da være så rødforskjøvet at det ikke lenger var lys. Vi vil her tilføye enda et moment som taler mot at natt-himmelen skulle være lys. Som nevnt foran har sannsynligvis universet endelig alder og på grunn av den endelige hastigheten til lyset betyr det at det er grenser for hvor langt ut i universet vi kan se. Dessuten har alle stjerner endelig levetid og vi vil derfor se enkelte av de fjerneste områdene slik de var før stjernene ble tent.
Et annet beslektet resonnement bygger på at gravitasjonspotensialet et sted er summen av potensialene fra hver av de omliggende massene. Hvis da universet er uendelig stort vil universet inneholde uendelig stor masse og gravitasjonspotensialet vil da bli uendelig. Også dette argumentet er avhengig av visse forutsetninger som vi ikke skal gå inn på her.
Vi vil til slutt bare konkludere med at det er vanskelig å finne noe helt avgjørende argument som kan avgjøre om universet er endelig eller uendelig. Mange føler vel likevel at et endelig univers er lettest å forestille seg. Når vi skal se på hvordan universet muligens har forandret seg i tid vil vi tenke oss et endelig univers med positiv krumming.
C7: Oppgaver
1 Prøv å avgjør om de nedenfornevnte stoffene er uniforme og isotrope sett fra et sted i eller inni stoffene. Ikke vær for pirkete. Egentlig finnes det vel ingenting som er helt uniformt og isotrop.
a) Tømmerstokk
b) Melk
c) Garnnøste sett fra midten
d) Garnnøste sett fra et sted lenger ute.

2 Studer figuren til
høyre.
a) Sola har en overflatetemperatur på omkring 6 000 K. Omtrent ved hvilken
bølgelengde sender sola ut mest stråling?
b) Hvor mange ganger mer stråling med bølgelengde 10-5meter (infrarød
stråling) får vi fra et legeme med temperatur 6 000 K i forhold til et
legeme med temperatur 300 K (27°C).
c) Nedenfor vises Wiens forskyvningslov. lm er den bølgelengden som
legemet stråler mest ved og T er temperaturen målt i Kelvin. k er en
konstant: k= 0.0029mK.
T· lm= k
Bruk formelen til å finne hvilke bølgelengde et legeme med temperatur
1 000 K stråler mest ved. Hvordan stemmer dette med figuren?
d) Vil dette legemet sende ut
(ikke bare reflektere) synlig lys tror du?
Synlig lys har bølgelengde mellom 4 og 8•10-7 meter. I tilfelle, bli mer eller mindre enn 1/100
av det vi mottar fra et tilsvarende legeme
med temperatur 6 000 K ved 8·10-7 meter bølgelengde (tilsvare rødt lys)?
Tips: På en logaritmisk skala ligger 1 000 omtrent midt mellom 300 og 3 000.
3 Hvis vi tenker oss at jorda er blitt til ved at stoffene på jorda har blitt
trukket sammen fra et svært stort område på grunn av gravitasjonskrefter vet vi at dette innebærer at den potensielle energien har avtatt. Hvis vi antar at tettheten er den samme overalt i jorda finnes det en formel som sier at den potensielle energien er E
= -(3/5)GM2 /R (Gravitasjonsenergi). Gravitasjonsenergien for partikler som er langt borte fra hverandre er til sammenlikning omtrent lik null
(r er da svært stor).
a) Regn ut gravitasjonsenergien for jorda.
b) Hvis vi antar at varmekapasiteten for jorda er 450 J(pr. K og kg) at jorda har blitt til fra ei større støvsamling med gravitasjonsenergi omtrent lik null, at temperaturen opprinnelig var 0 K og at all den frigjorte energien er blitt i jorda i form av varme. Hvilke temperatur ville jorda
da ha hatt? I solas kjerne regner vi med at temperaturen er ca 15•106K.
(Nødvendige data i
tillegg)
4 a) Prøv å beskrive hvordan to personer vil oppleve sin egen og den
andres situasjon hvis person a forblir langt borte fra det sorte hullet mens person b beveger seg sakte mot det. Vi forutsetter at de heile tida
kan se hverandre. Merk at rom-kontraksjonen (Dr->0) for en nær det sorte
hullet sett fra en som er langt borte, bare skjer i retningen mot det sorte hullet.
b) Hvordan tror du det vil føles for en uheldig romfarer i et romskip uten
vinduer å ramle inn i et sort hull? Anta at romskiper er lite og at ekvivalensprinsippet gjelder.
(det vil si at romfareren ikke kan
skille mellom krefter forårsaket av gravitasjon og akselerasjon) (Mer om dette i tillegget om den generelle relativitetsteorien.)
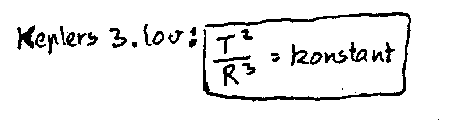
5 Keplers tredje lov sier at forholdet T2/R3 er det samme for
alle planetene rundt sola. T er tida for ei runde omkring sola og R er gjennomsnittsavstanden til sola fra planeten.
a) Hvis vi i stedet for å måle T i sekund måler den i år som jo er jordas
rundetid rundt sola, og istedet for å måle R i meter måler
den i AU som er
gjennomsnittsavstanden fra jorda til sola (1 AU = 1.5•1011 m) blir konstanten
ovenfor lik 1. Beregn utfra dette Jupiters baneradius når du far oppgitt at rundetida
for Jupiter er 11.9 år.
b) Når man beregner avstanden til ei stjerne ved hjelp av parallaksmetoden måler man først den maksimale vinkelen som ei stjerne synes å flytte seg på himmelen i løpet av et år (v). Halvdelen av denne vinkelen er da stjernas parallaks. Man kaller så den avstanden som tilsvarer en parallaks på ett buesekund for en parsek. Beregninger viser at en parsek er lik 3.26 lysår. Den nærmeste stjerna har en parallaks på 0.76 (a-Centauri). Beregn avstanden til denne stjerna i lysår.
c) Nedenfor vises forholdet mellom den tilsynelatende og den absolutte lysstyrken for to kjente stjerner. Hvis vi tenker oss at vi kunne flytte stjernene som vi ville, vil produktet I·R2 altid være konstant for ei bestemt stjerne. Den absolutte lysstyrken til ei stjerne står da for den lysstyrka vi ville observere hvis stjerna var plassert i en på forhånd valgt avstand som vi her kan kalle standardavstanden.
|
|
Tilsynelatende lysstyrke (I) |
Absolutt lysstyrke |
Avstand (lysår) |
|
a-Centauri |
57 |
1 |
4.3 |
|
Polarstjerna |
7 |
2500 |
|
Hvordan er avstanden til a-Centauri i forhold til den valgte standardavstanden? Hva med avstanden til Polarstjerna?(større eller mindre) Kan du finne standardavstanden ved hjelp av tallene for a-Centauri? Hva er standardavstanden målt i parsek? Finn til slutt avstanden til Polarstjerna utfra tallene ovenfor.
6 Vår galakse kan sammenliknes med en diskos med en diameter på ca.100 000 lysår. Galaksen dreier omkring tyngdepunktet.
a) Vil stjernene under dreiinga ligge fast i forhold til hverandre slik at alle stjernene har samme rundetid? Tenk på Keplers tredje lov og hvordan planetene dreier rundt sola.
b) Solas rundetid i Melkeveien er beregnet til å være 2·108 år. Hvor mange ganger skulle den da ha gått rundt hvis den ble til for ca. 5•109 år siden?
c)
Beregninger ved hjelp av radioastronomi viser at Melkevegen er en spiralgalakse omtrent slik som figuren nedenfor viser. Med bakgrunn i det som er kommet fram ovenfor, er der noen problemer med å anta at Melkevegen har dreid i mer enn 5·109år?

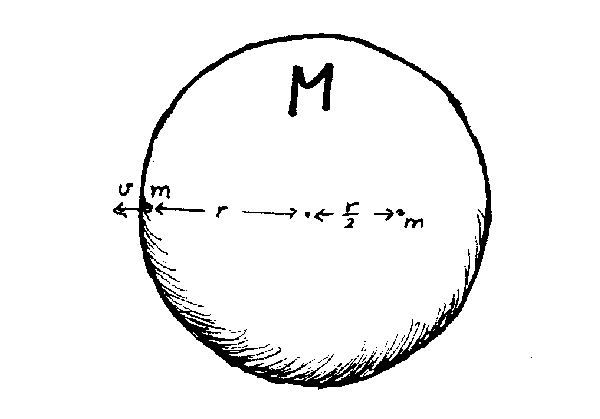
7 a) Vis ved hjelp av Newtons 2. lov og gravitasjonsloven at vi har følgende sammenheng mellom Melkeveiens masse innenfor sola
(M), solas baneradius i melkevegen (R) og solas hastighet (v): v2 = GM/R. Hvis vi antar at sola går i sirkelbane har vi: a = v2/R.
b) Bruk formelen ovenfor til å beregne
massen av Melkevegen hvis vi antar at massen utenfor sola er neglisjerbar
i forhold til den som er innenfor R = 2.8·1020m (=30 000 lysår),
v = 3·105 m/s
8 Tenk deg en stor kuleformet boks i et uniformt ekspanderende
univers. Massene i boksen er altså noenlunde jevnt fordelt og hastigheten
til massene er proporsjonal med avstanden fra sentrum i boksen. Totalmassen i boksen er M, radien r og hastigheten ved kanten av boksen er v.
a) Finn et uttrykk for den mekanisk
energien(Em) til en liten masse m ved
kanten av boksen.
b) Finn tilsvarende et uttrykk for den mekaniske energien til en masse lik m
som befinner Beg i avstanden r/2 fra sentrum i boksen. Husk at man i dette tilfellet bare skal ta hensyn til den massen som ligger innenfor ei
kule med r/2 som radius når man beregner den potensielle energien.
c)
Beskriv hvordan den mekaniske energien varierer for ulike masser i den ovennevnte boksen når krummingen er positiv, null og negativ.

9 Ifølge termodynamikkens første hovedsetning, kan ikke energi forsvinne. Ved pilene nedenfor skjer det en overgang fra en energiform til en annen.
a) Forklar hvilke energiformer som er involvert. Aktuelle energiformer er kinetisk energi,
potensiell energi, elektrisk energi, kjemisk energi, termisk energi(varme), strålingsenergi og masse.
b) b) Det meste av den energien vi bruker her på jorda kommer opprinnelig fra sola. Hvis vi tenker oss solsystemet som et lukket system; er det da mulig å levere energien tilbake til sola? Begrunn svaret.
c) Figuren ovenfor viser stor og liten orden i tre forskjellige slags former. Kan man si at orden er en betingelse for at det skal være levelig? Hvis ingenting gjøres for å motvirke naturens gang, hva tror du vil skje i tilfellene ovenfor? Hva er det egentlig som kan øke ordenen omkring oss og i universet?
d) Prøv å beskrive hvordan forholdene på jorda vil utvikle seg når energitilførselen fra sola tar slutt.
10 De som antar at universet har positiv krumming antar da vanligvis at
radien i universet er størrelseorden 1010 lysår. Tenk deg at vi
komprimerer rommet til to dimensjoner. Da kan vi tenke på universet som
overflata av ei kule som har radius 10 lysår.
a) Dersom universet er statisk(konstant størrelse), hvor lang tid ville
da lyset trenge for å nå rundt hele universet og komme tilbake fra
motsatt retning? For å få et bedre inntrykk av størrelsesforholdene i universet vil
vi tenke oss at vi forminsker det til ei kule med radius 100 meter. Det vil si at l
mm tilsvarer 100 000 lysår. Nedenfor følger noen avstander.
Diameteren av melkevegen 100 000 lysår.
Diameteren av vår galaksehop 5•106 lysår.
Avstanden til Virgo (nær galaksehop) 64·106 lysår.
Avstanden til Hydra (fjern galaksehop) 3·109 lysår.
b) Hva tilsvarer dette i vårt miniunivers? Hvilke målemetoder tror du
er brukt for å komme fram til disse tallene?
11 Nå vet vi egentlig ikke om universet har positiv krumming.
a) Hvilke andre muligheter finnes for form og størrelse på universet?
b) Er det mulig å tenke seg at det finnes ei grense i universet som skiller oss fra et annet univers?
c) Hvordan vil forholdet mellom vårt univers og et firedimensjonalt univers som inneholder vårt univers være? Er det mulig å tenke seg noen form for komunikasjon mellom dem?