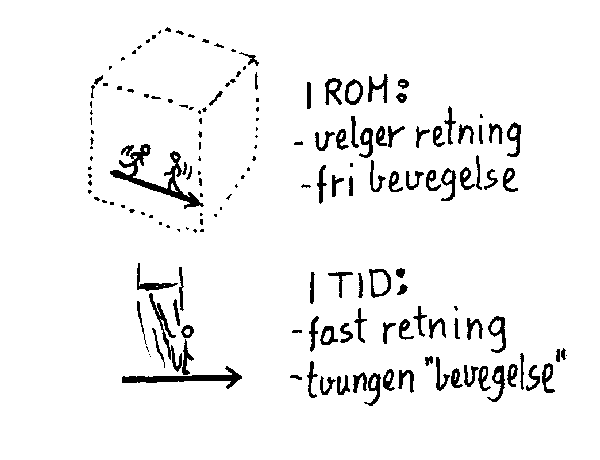
A: Begrepene rom og tid
A1: Begrep i dagliglivet



Kosmologi er læren om universet. Mens astronomene studerer det som finnes i universet er kosmologene mer opptatt med å finne ut hva universet egentlig er. Dessuten er man i kosmologien også opptatt med å finne ut hvordan universet har vært i fortida, og hvordan det vil bli i framtida. Det er altså dette som er temaet for de følgende sidene. Men først skal vi si noe generelt om begreper og bruken av dem. Når vi skal forklare eller beskrive noe, bruker vi alltid ord eller begreper som tilhørerne forstår. Hvis tilhørerne ikke forstår de ordene som brukes,vil de heller ikke forstå det vi prøver å forklare dem. La oss se på et eksempel. Et utsagn som; "Jeg drakk et glass melk til frokost " vil umiddelbart bli forstått og noen grundig analyse av utsagnet er ikke nødvendig. Dette fordi begrepene og også den situasjonen som beskrives er velkjent for de fleste.
I kosmologien bruker man også vanlige ord og begreper. Men kosmologiske beskrivelser er som regel ikke så lette å forstå som utsagnet ovenfor. Grunnen er hovedsaklig at vi ikke har noen direkte erfaringer med det som kosmologien beskriver. Det er derfor spesielt viktig i kosmologien at man har en klar forståelse for hva ord og begrep egentlig betyr. Vi vil derfor her først ta for oss noen av de mest grunnleggende begrepene i kosmologien. Når disse er forstått blir det lettere å forstå de forskjellige beskrivelsene av universet som følger seinere.
Hva er så grunnleggende begrep? Se på utsagnet ovenfor. Hva handler det egentlig om? Studerer vi det nærmere, finner vi kanskje at det handler om et stoff som heter melk. Felles for alle stoff er at de har en masse som forteller noe om vekt eller tyngde. Som vi skal se seinere er masse et sentralt begrep.
Dessuten sier utsagnet noe om hvor mye melk somble drukket."Et glass" angiret bestemt volum, nemlig det volumet som er i et glass. Et annet ord for volum er rom. Dette begrepet kommer vi til å bruke mye i det følgende. Her vil vi bare nevne at rom kan ha en størrelse (volum) og dessuten er det mulig å bestemme ei plassering i et rom.
Utsagnet forteller også noe om når begivenheten hendte. Selv om "til frokost" kanskje er en litt upresis tidfesting, så gir detlikevel ei tid for hendelsen, Utsagnet "Jeg drakk" fortellerblant annet at det har vært en kraft til stede. Den har sin årsak i "jeg"og det er glasset som blir påvirket.
Eksempelet ovenfor viser at fysiske grunnbegrep "følger oss" i hverdagen selv om vi ikke tenker så mye over det. Deter litt interessant å tenke påat dissefire begrepene (rom, tid, masse og kraft)også er grunnbegrep i kosmologien.Vi skal så studere dissebegrepene nærmere.
A2: Rom
Det kanskje viktigste begrepet i kosmologien er rom-begrepet. Men hva er det egentlig? Det er vanskelig å forklare hva det er fordi det er så altomfattende. En beskrivelse av rom-begrepet vil på en måte forutsette at rombegrepet er kjent fordi alt omkring oss "er rom". Vi er plassert i et univers som er uløselig knyttet til rom-begrepet, og vi kan vanskelig forestille oss en tilværelse uten rom. Vi skal i det følgende prøve å forklare rombegrepet ved en slags matematisk tilnærmingsmetode.

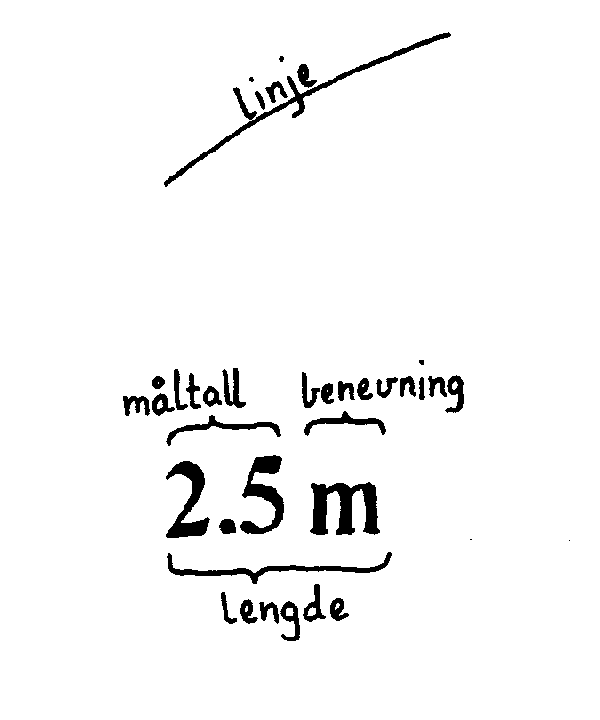

PUNKT Vi vil to utgangspunkt i et punkt. I matematikken er et punkt så lite at uansett hvor mye det blir forstørret vil det forbli et punkt. Det har altså ingen utstrekning eller volum. Nå vil kanskje noen innvende at det som ikke har volum, ikke kan eksistere. Dette er vel egentlig riktig (filosofisk problem), men i matematikken har man bruk for slike punkter. Tilsvarende har man innført begrepet null (0), og man kan da si at et punkt har null volum.
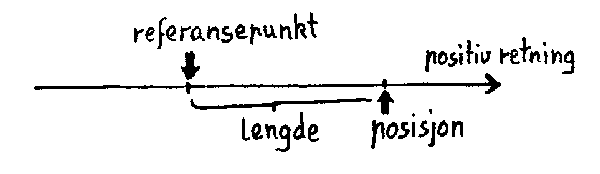
LINJE. Ei linje kan vi tenke på som ei samling av uendelig mange punkter som ligger på rekke. I motsetning til et punkt har ei linje ei utstrekning, men bare i ei retning. Med ei retning mener vi her både positiv og negativ retning. I alle andre retninger er utstrekningen lik null. Fordi linja har ei utstrekning sier vi ofte at den har en dimensjon. Den utstrekningen som linja har kaller vi lengde. Men hva er så egentlig lengde? Når vi måler ei lengde får vi f.eks. resultatet 2.5 meter. Vi sammenlikner da egentlig lengden vår med en standardlengde som vi har valgt på forhånd. Meter er en standardlengde som brukes over hele verden. Vi kan bare måle lengder ved å sammenlikne dem med andre lengder. Dette uttrykkes ved hjelp av et måltall (2.5) og en benevning (m), hvor måltallet angir hvor mange ganger større/mindre den målte linja er i forhold til standardlinja. Merk ellers at ei lengde er den samme uansett hvor vi flytter den eller om vi uttrykker den med en annen benevning. Ei lengde er absolutt i den forstand at en forblir uforandret uansett ytre forandringer. Nå forteller relativitetsteoriene om unntak fra denne regelen. Disse skal vi komme tilbake til siden, men foreløpig vil det være en fordel å tenke på lengder som noe absolutt. Ved hjelp av lengde kan man også bestemme en posisjon på ei linje forutsatt at man har et referansepunkt. Dette gjøres ved å oppgi et fortegn (+ eller -) og ei lengde. Da posisjonen er avhengig av referansepunktet man har valgt, vil posisjoner alltid være relative.
Nå passer det her å si litt om uendeligbegrepet. Akkurat som vi i matematikken har innført begrepet null, så har man også innført begrepet uendelig(∞). Ei linje med uendelig lengde vil da være lenger enn alle tenkte lengder. Eller sagt på en annen mate: Uansett hvor langt man beveger seg langs ei slik linje så vil man aldri finne enden. Nå er det vanskelig for var tanke å fatte hva dette begrepet egentlig betyr. I matematikken er det imidlertid et viktig begrep og vi kommer også til å bruke det mye her. I kosmologien blir det aktuelt når man skal beskrive det som er bortenfor/utenfor det kjente universet.



Det er ogsåviktig å være klar over hva som egentlig ligger i begrepene rette og krumme linjer. Dette er egentlig begrep som ligger utenfor den ene dimensjonen som linja representerer. Med andre ord: Et endimensjonalt vesen(et vesen som lever i en dimensjon og bare kjenner tit denne) ville ikke forstå hva vi mener når vi snakker om krumme linjer. For dette vesenet vil bade krumme og rette linjer være like rette. Det er fordi vi ser linja som en del av vårt tredimensjonale rom at vi kan skille mellom rette og krumme linjer.
Så kort om hva som er forskjellen på uendelig og uten ende: Tenk deg en sirkel. Det er ei linje som er uten ende, men samtidig er den ikke uendelig lang. Et endimensjonalt vesen på sirkelen ville kunne trekke den slutninga at at linja er endelig lang hvis det kom tilbake til utgangspunktet når det beveget seg i ei retning. Men det ville fortsatt ikke "se" krummingen.
FLATE Hvis vi nå utvider antall dimensjoner til to, får vi ei flate. Ei flate har utstrekning i to retninger(derav to dimensjoner). Men den har fortsatt null utstrekning i ei retning. Det vil si at den er uendelig tynn. Utstrekninga til ei flate kaller vi areal. Som for linja må vi også her velge et standardareal for å kunne bestemme størrelsen på forskjellige flater. Det er praktisk å velge et areal som er 1 x 1meter som standardareal. Benevningen blir da m2 og kalles kvadratmeter . Grunnen til dette valget av standardareal kommer kanskje tydeligst fram når man skal bestemme arealet av en rettvinklet firkant. Ved å multiplisere måltall og benevning for to sider får man arealet "rett ut". Areal er absolutt liksom lengdene er absolutte.
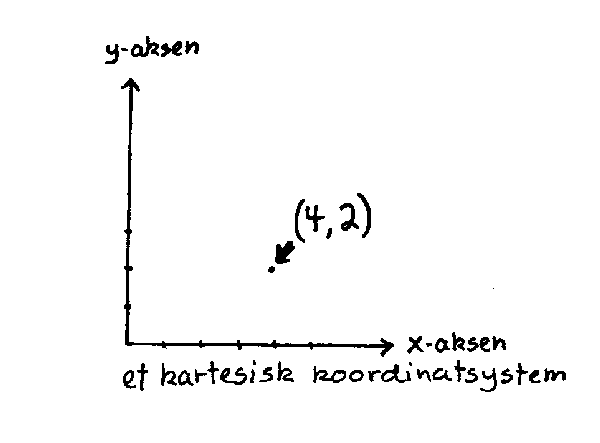
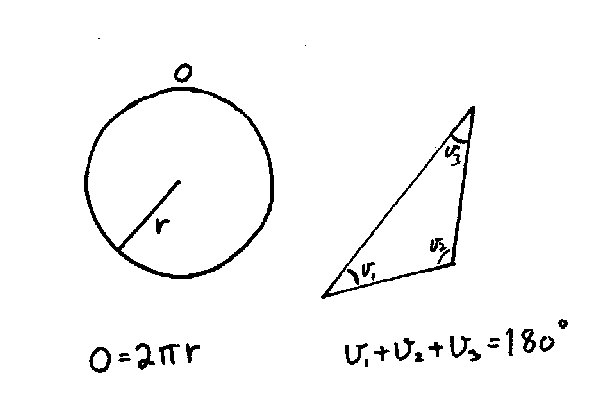
Når det gjelder posisjonsbestemmelse på ei flate, trenger man to lengder(med fortegn) og et koordinatsystem. Vanligvis velges et koordinatsystem med to akser som står normalt på hverandre. Aksene kalles da x- og y-aksen. Merk ellers at posisjonsbestemmelsen alltid er relativ til koordinatsystemet. Posisjoner. kan også bestemmes ved hjelp av vektorer. Nå er metodene ikke så viktige i denne sammenhengen, så vi skal ikke gå noe nærmere inn på disse her. Det er derimot litt vesentlig at man har en forståelse for hva som ligger i uttrykket at ei flate har to dimensjoner. Det kan kanskje være en fordel å tenke seg at ei flate er "oppbygd" av to uavhengige linjer (eks: x-aksen og y-aksen).
Så litt om egenskapene til ei flate. I dagliglivet brukes todimensjonale flater mye. Skrift, bilder og figurer blir ofte fremstilt på ei flate fordi dette er mest praktisk. På ei linje er det lite vi får plass til, og tredimensjonale fremstillinger er kompliserte og upraktiske i de fleste daglige situasjoner. Den delen av matematikken som er mest knyttet til flater, kalles geometri. For eksempel er sirkel og trekant geometriske figurer i ei todimensjonal flate. Som de fleste vet, er det bestemte regler eller lovmessigheter som gjelder i geometrien. Eksempler på disse er: Omkretsen av en sirkel: 0 = 2π r og summen av vinklene i en trekant er 180 grader. Vi skal i det følgende se at dette ikke alltid er tilfelle, men først må vi definere hva vi mener med ei rett linje.
Merk først at det er nødvendig å ha minst to dimensjoner for å definere ei rett linje. For et vesen i en dimensjon vil det bare være ei linje, og han vil ikke ha noen forestilling om hva som er forskjell på rette og krumme linjer. Merk dessuten at det som vi kaller rett i dagliglivet; linjaler, lysstråler og lignende, er rett i vår tredimensjonale verden. Det er imidlertid ikke slik at våre rette linjer nødvendigvis må være rette i flere eller færre dimensjoner. Så til definisjonen på ei rett linje: Ei rett linje er den kort-este vegen mellom to punkter. Det er klart at denne definisjonen stemmer med hva vi betegner som rett i vår tredimensjonale verden. Men hva med den todimensjonale verden som ei flate er?
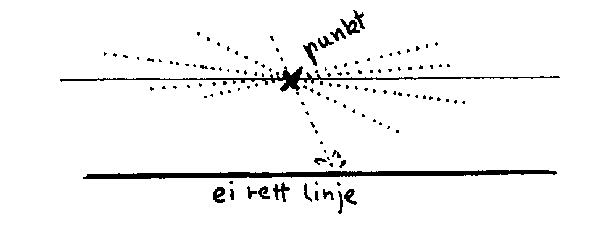
Nå finnes det i geometrien et grunnleggende aksiom som vi kort skal nevne her. Det sier at det gjennom et punkt utenfor ei rett linje kan trekkes ei og bare ei, rett linje som ikke skjærer den første linja. Nå kan det vises matematisk at hvis dette er oppfylt, så vil de geometriske lovene ovenfor gjelde. Selve aksiomet derimot kan ikke bevises. Det finnes nemlig flater hvor dette aksiomet ikke gjelder. I de tilfellene hvor aksiomet gjelder kalles geometrien euklisk. Nå kan dette i første omgang synes å være ganske uaktuelt for vårt tema. Grunnen til at vi her legger forholdsvis mye vekt på todimensjonal geometri er at den likner på vår tredimensjonale romgeometri på mange måter. Dessuten kan vi fysisk forestille oss hvordan krumme flater ser ut. Det kan vi imidlertid ikke gjøre når det seinere blir snakk om krumme rom, og våre todimensjonale betraktninger vil da kunne hjelpe oss til å forstå hva som ligger i begrepet krumming. Merk ellers at vi fortsatt holder på med todimensjonale flater og krumminga er altså en egenskap ved denne flata. Når vi her skal prøve å få fram hva ei krum flate er, vil vi tenke oss flata som en del av vårt tredimensjonale rom. Merk ellers den direkte sammenhengen som er mellom aksiomet og den aktuelle krummingen.
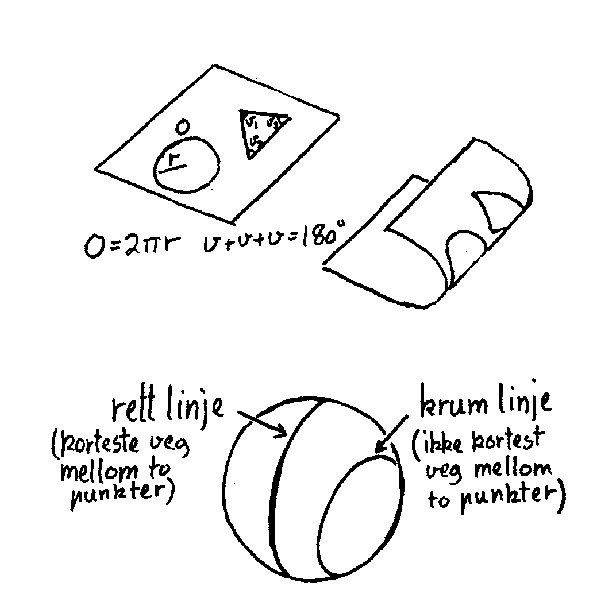
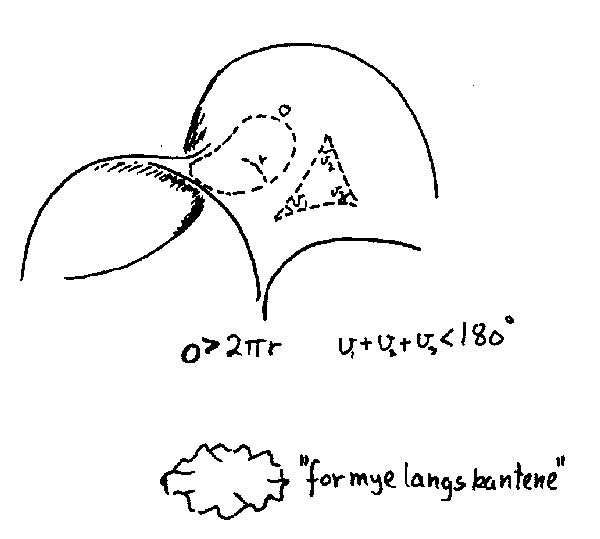
PLAN FLATE (euklidsk, null krumming) Dersom aksiomet foran gjelder, sier man at flata er plan. På denne flata får vi så alle de kjente lovene som vi kjenner fra skolen(0=2πr osv.). Merk at dette også gjelder om vi bøyer flata i våre tre dimensjoner(se fig.). Et vesen i den todimensjonale flata ville altså ikke merke noe forskjell. Det eneste vesenet kan si er at flata er plan, f.eks. fordi vinklene i en trekant er 180 grader til sammen.
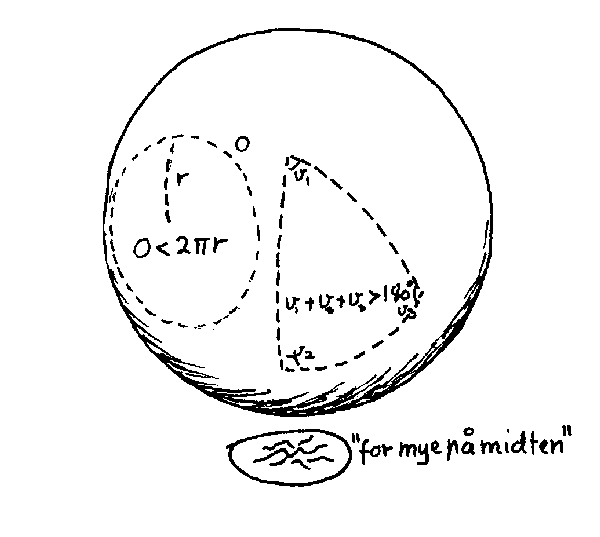
KULEFORMET FLATE (positiv krumming) Hva så om aksiomet foran ikke gjelder? En mulighet er at det ikke finnes noen rette linjer som ikke skjærer den opprinnelige linja. En slik situasjon har vi på ei kuleflate. Alle rette linjer her er ifølge definisjonen foran, storsirkler. Det vil med andre ord si at alle rette linjer på ei kuleflate vil dele flata i to like store deler. Dette betyr igjen at det ikke er mulig å tegne to rette linjer på ei kuleflate som ikke skjærer hverandre. Vi kan da f.eks. si at ei flate hvor alle rette linjer skjærer hverandre, har positiv krumming. Utfra dette kan man så utlede andre lover. For eksempel vil omkretsen av en sirkel alltid være mindre en 2πr, og vinkelsummen i en trekant vil alltid være større enn 180 grader. Dette gjør igjen at et vesen på denne flata kan si at flata er krum hvis f.eks. vinkelsummen i en trekant er større enn 180 grader. Merk ellers at ei krum flate aldri kan gjøres plan. Hvis vi forsøker på det vil vi oppleve at det blir "for mye på midten". Merk også at ei krum flate kan være uten ende selvom den ikke er uendelig stor (kuleflate).
SADELFORMET FLATE (negativ krumming) Som noen kanskje forstår utfra sammenhengen, finnes det en type flate til. I disse flatene vil det finnes mange rette linjer gjennom et punkt utenfor ei rett linje som ikke skjærer denne linja. Utfra dette kan man så utlede endel lover. Blant annet vil omkretsen av en sirkel være større en 2πr, og vinkelsummen i en trekant vil være mindre enn 180 grader på ei sadelformet flate. Hvis vi prøver å gjøre ei slik flate plan, vil man oppleve at man får "for mye langs kantene".
Til slutt i avsnittet om flater vil vi bare understreke at vi gjorde bruk av vart tredimensjonale rom for å forklare hva som menes med krumming i to dimensjoner. Når vi seinere snakker om krumme rom, kan det tilsvarende være nyttig å tenke på denne krummingen som noe som skjer i fire dimensjoner. Fordi vi ikke kan forestille oss fire dimensjoner vil vi senere "komprimere" det tredimensjonale rommet til ei flate og illustrere rommets krumming på tilsvarende måte som vi har gjort her.


ROMHvis vi nå utvider til tre dimensjoner, får vi det vi kaller rom. Det tredimensjonale rommet har altså ei utstrekning i tre retninger. Vår virkelighet er tredimensjonal og det er for oss opplagt at alle tre dimensjonene trengs. Uten tre dimensjoner ville vi ikke hatt noe fysikk eller biologi. Vi ville altså ikke eksistert. Som nevnt er vår tanke uløselig knyttet til rombegrepet, og dette gjør det litt vanskelig å forstå hva vårt tredimensjonale rom egentlig er. I kosmologien er det viktig å holde fast på den matematiske forståelsen med blant annet enheter. En enhet for volum kalles kubikkmeter(m3), og det som måles kalles volum. Ved å bruke denne enheten kan man f.eks. finne volumet av en kloss ved å måle lengde, bredde og høyde og så multiplisere sammen måltall og benevning . Volum er en absolutt størrelse liksom lengde er det.
Når vi skal bestemme en posisjon i rommet, trenger vi tre lengder og et referansesystem å bestemme posisjonen i forhold til. Alle posisjoner i rommet blir da relative i forhold til det valgte referanse systemet. Det vanligste referansesystemet er et rettvinklet koordinatsystem hvor vi kaller aksene x-, y- og z-aksen. I enkelte situasjoner kan det være hensiktsmessig å bruke andre koordinatsystem. Et eksempel er kulekoordinater hvor man bruker to vinkler og ei lengde for å bestemme posisjoner. Vi skal ikke gå inn på de forskjellige koordinatsystemene her. Det kanvære nyttig å betrakte rommet som sammensatt av tre lengder slik det kommer til uttrykk i volumenheten m3 og posisjonsangivelsen (Ll,L2,L3) hvor Ll, L2 og L3 står for lengdene langs henholdsvis x, y og z-aksen. For å understreke at vi har med rom å gjøre, vil vi i det følgende omslutte endel av figurene med en "boks" uten at vi dermed tar noen stilling til form og størrelse på rommet.
Når vi nå har gjennomgått en slags matematisk forklaring på hva rom er, er det naturlig å si litt om de grensene som finnes for rommet eller universet. Som det går fram av det foregående endte vivår dimensjonsutvidelse ved tre dimensjoner.Kan det da tenkes at det finnes et slags superrom med fire dimensjoner? Fordi våre vitenskapelige metoder er knyttet til våre tre dimensjoner, kan vi ikke på vitenskapelig grunnlag utelukke denne muligheten. Selv omman ofte brukertida som en slags fjerde dimensjon i endel matematiske beregninger, så betyr ikke det at tida er den fjerde dimensjonen vi snakker om her. Om det finnes en fjerde dimensjon er og forblir et filosofisk/religiøst spørsmål som vitenskapen ikke kan avgjøre. Om det skulle vise seg at vårt tredimensjonale rom er krummet så betyr ikke dette nødvendigvis at det finnes en fjerde dimensjon.
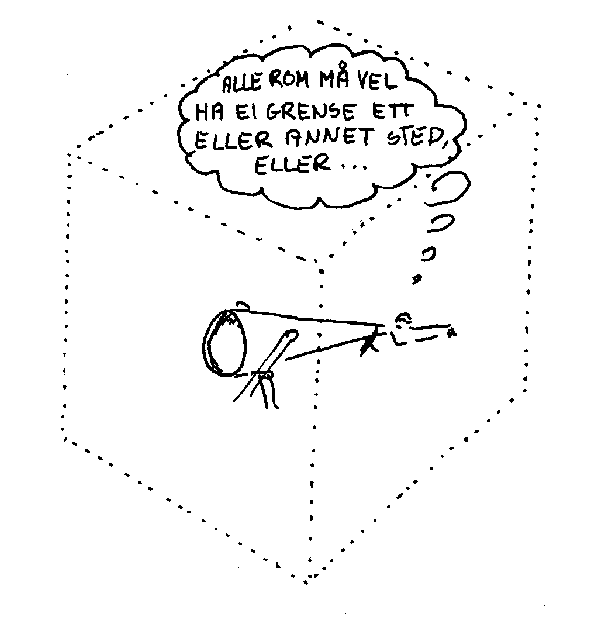
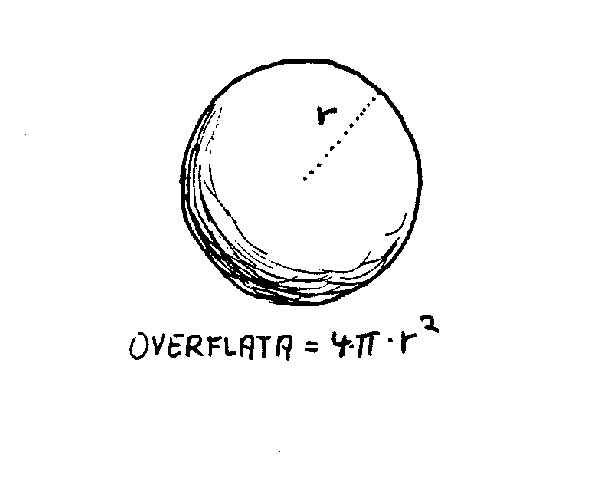
Den andre grensa vi kan tenke oss når det gjelder vårt rom, er den som har med størrelsen på rommet å gjøre. Hvor stort er egentlig universet? Vi har foreløpig ikke observert noen grenser for universet og det finnes da ulike muligheter. En mulighet er at universet er uendelig stort. Alternativet til det er at universet er endelig stort. Hvis det siste er tilfelle, finnes det igjen to muligheter. Enten stopper universet et eller annet sted ved ei grense, eller så har universet positiv krumming. Vi skal komme tilbake til disse mulighetene seinere. Her vil vi bare kort se litt på hva det betyr at rommet er krummet. Ville vi ha noen muligheter for å konstatere at vårt rom f.eks. har positiv krumming? En mulighet er å sjekke opp lovene i romgeometrien. Vi har f.eks. en lov som sier at overflaten av ei kule er 4πr2 . Hvis rommet har positiv krumming, skulle vi vente at overflata var litt mindre. Nå er det imidlertid slik at hvis rommets krumming er liten i forhold til størrelsen på testkula vår, vil avviket fra formelen ovenfor være så liten at det ikke er mulig å påvise det. En annen mulighet for å kunne påvise at rommet har positiv krumming, er å sende f.eks. ei lysstråle avsted i ei retning, og så vente å se om den kommer tilbake fra motsatt retning. Av ulike grunner som vi skal komme tilbake til seinere, er heller ikke dette noen brukbar metode i vårt univers. Nå er det imidlertid slik at hvis Einsteins generelle relativitetsteori er sann, så gir den oss en annen metode for å avgjøre problemet ovenfor. Vi skal komme tilbake til dette seinere. Her vil vi bare konstatere at det ikke finnes noen direkte metoder for å avgjøre krumminga til universet.
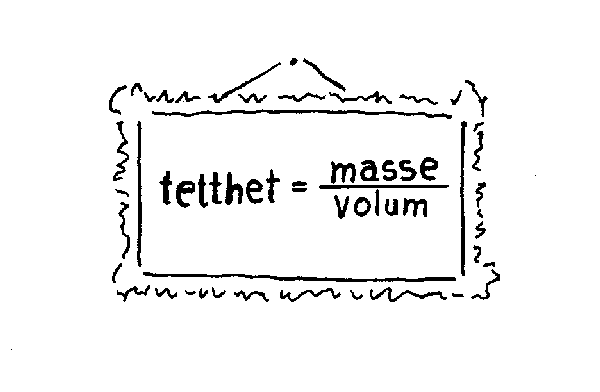
TETTHET.Vi vil til slutt i denne innføringa i rom-begrepet kort si noe om begrepet tetthet. Den kanskje viktigste egenskapen ved rommet er at det kaninneholde noe. Vi nevnte tidligere at det er knyttet en masse til alle fysiske ting. Vanligvis tenker man på massen som vekten eller tyngden av tingen. Vi skal komme mer tilbake til massebegrepet seinere. Her vil vi anta at begrepet er kjent. Så tilbake til tetthet-begrepet. Definisjonen på tetthet er masse dividert på volum eller masse pr. volumenhet.Al1e ting (også universet) har en tetthet og størrelsen av denne er ganske avgjørende. Utfra definisjonen ovenfor ser vi at hvis volumet avtar, vil tettheten øke for samme masse. Dette er en grunnleggende sammenheng i kosmologien. Både i universet som helhet og i de enkelte stjerner regner vi med at massen er tilnærmet konstant. I praksis blir det da volumet som blir det avgjørende når man skal si noe om hvordan universet egentlig er. Merk ellers at det teoretisk er mulig å tenke seg et volum uten masse, men ikke omvendt. Dette er ellers et eksempel på at rom som er et grunnleggende begrep, inngår i et annet begrep. Dette vises også av benevningen for tetthet som f.eks. kan være kg/m.
A3: Tid (time)
På samme måte som rom er et grunnleggende begrep, er også tid et grunnleggende begrep. Vi kan ikke tenke oss en tilværelse uten tid. Samtidig er det vanskelig å si hva tid egentlig er. Umiddelbart vine kanskje noen tenke på et fotografi som et eksempel på at tida er "utsjaltet". Så enkelt er det imidlertid ikke. For det første beveger lyset fra fotografiet seg med endelig fart, og uten tid ville vi ikke kunne se fotografiet. Nå vil nok noen mene at fotografiet likevel må kunne eksistere selvom det ikke er tid. Problemet her er at fotografiet er en samling av mange punkter, og uten tid ville det være umulig med noen som helst slags kommunikasjon mellom disse. Det betyr igjen at ingen ville være i stand til å kunne avgjøre om punktene representerte et bilde eller ikke. Vi vil derfor betrakte tida som et grunnleggende begrep som er helt nødvendig i naturvitenskapen. Tid kan måles ved hjelp av klokker ol. På samme måte som ved lengder har man valgt et standard-tidsrom.

Sekund er den vanligste enheten, og andre tidsrom måles da ved å sammenlikne dem med et-sekund. Selve tidsrommene regnes til vanlig som absolutte størrelse. De kan da "flyttes" både i rom og tid uten at de forandres. Nå er det imidlertid endel som mener at det ikke er rom og tid hver for seg som er absolutt, men en kombinasjon av disse. Dette følger av den spesielle relativitetsteorien. Vi skal komme tilbake til dette seinere. Her vil vi bare konstatere at vi trenger noen grunnleggende begrep som er absolutt for at vi i det hele tatt skal kunne si noe om noe.
Når det gjelder tidspunkt, så er disse relative i forhold til et referansetidspunkt. Et eksempel på dette er var tidsregning som oppgis i antall år før eller etter Kristi fødsel. Som det går fram av det som er nevnt til nå, er det flere likheter mellom rom-og tidsbegrepet. I begge tilfellene må vi velge enhet (m,s), og i begge tilfellene snakker vi om positive og negative retninger. Det er imidlertid en viktig forskjell her, som også på en måte hjelper oss å forstå hva tida egentlig er. I rommet velger vi den positive retninga, og så kan vi bevege oss i positiv og negativ retning som vi vil. Når det gjelder tida er den positive retninga fast fra naturens side, og vi blir alle "skjøvet med" enten vi vil eller ikke. Vi kan altså ikke stoppe tida eller bevege oss bakover i tida. Dette fenomenet kalles "the arrow of time" i engelsk litteratur.

Her melder det seg imidlertid et problem. Alle er enige om at vi "beveger oss" i tid, men hva er det egentlig som"skyver på" eller hvordan kan vi egentlig vite at, vi "beveger oss"? Hva er referansesystemet som vi kan måle tida i forhold til? Hva er det egentlig som gjør at ei klokke er brukbar til å måle tid med? Fordi var tanke er så uløselig knyttet til tida, er det vanskelig for oss å stille oss "på utsida" og betrakte tida "utenfra". Nå kunne det vært sagt mye om dette problemet, og sannsynligvis ville vi aldri komme helt til bunns. Det er imidlertid en klar sammenheng mellom tida og en naturlov som kalles Termodynamikkens 2. hovedsetning eller entropiloven. Vi skal komme tilbake til denne seinere. Her vil vi kort si at loven i hovedsak sier at alt går mot uorden. Når det gjelder klokka, så betyr det f.eks. at energien som er lagret i fjæra er "mer ordnet" enn den varmen som blir resultatet når fjæra er gått ut. Her finner vi "the arrow of time" igjen i det at prosessen bare går fra potensiell energi i fjæra til varme,og ikke omvendt. Hvis vi et øyeblikk prøver å tenke gjennom hva slags prosesser/ hendelser som omgir oss til daglig, vil vi sannsynligvis finne ut at vi er omgitt av enveisprosesser hvor uordenen øker. Hvis vi f.eks. filmet ved som brenner eller noen som søler vann, vil vi se at dette er enveisprosesser dersom vi kjørte filmen bakover. Hvis det ikke var for denne"enveiskjøringa" i naturen hvor alt går mot uorden, så ville vi ikke kunne måle tida. Alt ville bli en slags tidløs rotete tilværelse. Mange forskere er enige om at hvis det ikke skjer noe uventet med universet, så vil det til sluts ende i en tilstand med maksimal entropi eller uorden. Alle klokker vil da ha gått ut og ingen vil da kunne måle tida. Om det fortsatt vil eksistere tid eller ikke er da mer et filosofisk spørsmål.

Før vi forlater tidsbegrepet,vil vi nevne en annen ting som skiller det fra rombegrepet. Som nevnt tidligere er det ikke noen problemer knyttet til å anta at ei linje "biter seg selv i halen". Når det gjelder vart tredimensjonale rom, så er det i prinsippet dette som skjer med alle linjer hvis krumminga er positiv. Man unngår på en måte problemene med et uendelig rom, og de problemene som er knyttet til å sette grenser for rommet, hvis man antar at alle linjer "biter seg selv i halen". Når det gjelder tida, så er det ikke så enkelt. Fordi entropien i universes øker, er det ikke uten videre mulig å tenke seg at tida "gjentar seg" ved å "bite seg selv i halen". Hvis dette var tilfelle, burde vi ha en periode hvor entropien avtok. En slik minkning av entropi er så langt vi vet "unaturlig". Det er derfor vanlig blant vitenskapsmenn å snakke om en begynnelse eller en skapelse av universet. Problemet for vitenskapen er da at den ikke kan si noe om det som var før begynnelsen, og følgelig heller ikke noe om årsaken til begynnelsen. Det skulle med andre ord bety at selve begynnelsen er overnaturlig eller utenomnaturen fordi vare naturlover ikke er brukbare lenger tilbake enn til begynnelsen.
A4: Rom-tid diagram
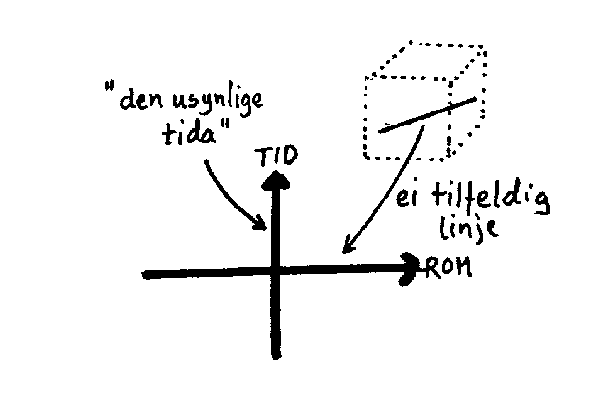
Nå er det slik at rom og tid alltid forekommer "samtidig" i naturen. Man har derfor innført et diagram som er mye brukt i kosmologien. Vi skal også her bruke dette rom-tid diagrammet endel, og vi vilgi en innføring i hva det egentlig er. Rom-tid diagrammet er et todimensjonalt koordinatsystem. Den ene aksen representerer da en vilkårlig linje fra vårt tredimensjonale rom. Man komprimerer med andre ord rommet til en dimensjon. Den andre aksen representer er da tida. Dette gir som vi skal se en ganske bra oversikt over endel praktiske situasjoner.
For å få fullt utbytte av dette diagrammet, er det nødvendig å forstå begrepet hendelse (eng:event ). Alt som foregår med oss og omkring oss foregår i rom og tid. En hendelse består da av en stedsangivelse og en tidsangivelse. Alle hendelser fåri utgangspunktet fire koordinater, en tidskoordinat(t) og tre romkoordinater(x,y,z). Disse er ofte satt sammen slik:(t,x,y,z). Hvis man derimot på forhånd har valgt ut ei linje i rommet som vi antar at alle hendelsene foregår langs, kan en hendelse oppgies slik:(t,r). R representerer da avstanden til hendelsen målt langs linja. Alle størrelsene ovenfor må angisrelativt til et referansesystem. I kosmologien brukes oftest "her og nå" som referanse.
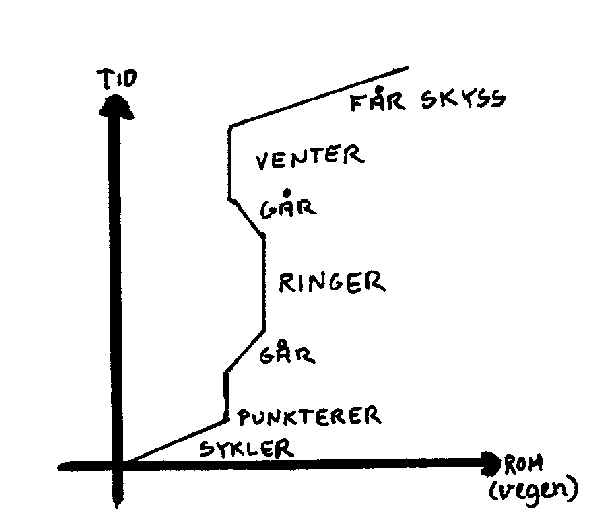
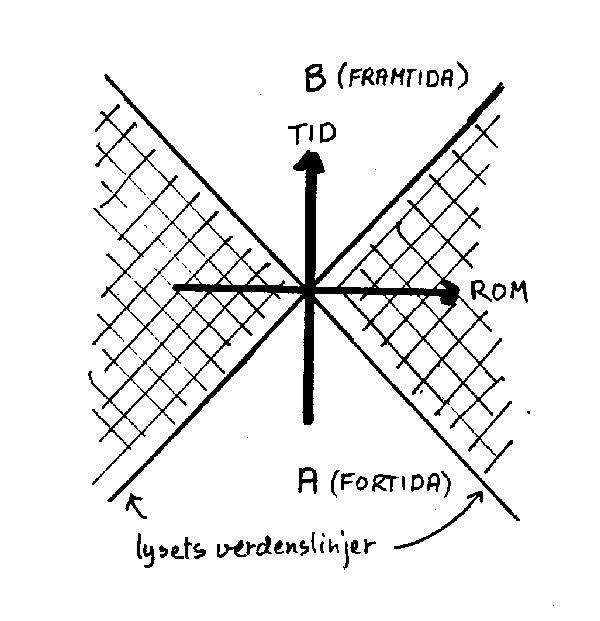
Et eksempel på hvordan ulike hendelser kan fremstilles i et rom-tid diagram er vist til venstre. Det viser hva som skjedde etter at Per syklet hjemmenfra klokka 12. Den linja som er tegnet kalles Pers verdenslinje. Hvert punkt på linja blir da hendelser.
Nå er det endel forhold man bør være oppmerksom på når det gjelder slike rom-tid diagram.'Nedenfor følger de viktigste.
(l) Merk at når man har "lagt tida ned på papiret", så er det ikke mer tid igjen utenfor papiret. Det betyr f.eks. at ei verdenslinje ikke "vokser" ettersom tida går. Både fortida og eventuelt framtida ligger allerede på papiret.
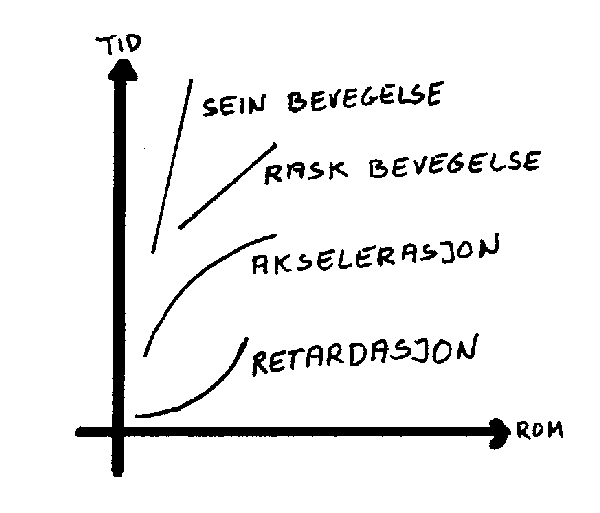
(2) Et rom-tid diagram gjør at man lett kan skille mellom rask og langsom bevegelse. Akselerasjon og retardasjon får sine karakteristiske verdenslinjer. Se figuren.
(3) Rom-tid diagrammer i kosmologien er oftest ordnet slik at det som beveger seg med lyshastighet, får en verdenslinje som har 45 grader i forhold til aksene. Det betyr i praksis at et sekund blir avsatt like langt som 300 000 000 meter på aksene (lyshastigheten = 300 000 000 m/s). Dette betyr at de fleste vanlige bevegelser får svært nær loddrette verdenslinjer. Nå er det imidlertid slik at det stort sett er lysets bevegelse i universet som er interessant for oss, og dette forholdet representerer derfor ikke noe problem i praksis. Siden lyshastigheten er den største hastigheten vi kjenner til, betyr det at vi ikke kan se eller få andre opplysninger om hendelser utenfor område A. Se figuren. Av samme grunn kan vi heller ikke formidle signaler (lyssignaler eller annet) til eventuelle mottakere som befinner seg utenfor område B, forutsatt at vi befinner oss "her og nå". Vi skal seinere komme tilbake til konkrete eksempler på bruk av dette diagrammet.
A5: Store og små størrelser
Til slutt i dette kapittelet vil vi kommentere en vanlig mate å angi størrelser på som ofte blir brukt i kosmologien. De fleste har en ganske bra forestilling om hvor lang en meter og en millimeter er, og hvor langt et sekund er. Når det derimot er snakk om størrelsen eller alderen på universet, vil de fleste få problemer med å forestille seg det. For mange vil alle avstander som er lenger enn avstanden til f:eks. månen være ufattelige. De gir derfor opp å forsøke å forestille seg de avstandene som finnes i universet. I kosmologien lager man seg bilder eller modeller av universet, og det er da nødvendig å være fortrolig med de størrelsene man operer med. Det er på en måte nødvendig å ha en indre referanseramme som man kan sammenlikne de oppgitte størrelsene med.
Før vi beskriver en mate å tenke avstander og tidsrom på, skal vi kort se på hvordan tallsystemet vårt er oppbygd. Så skal vi vise en måte å lage ei tall-linje som "når lenger"en det som er vanlig. Som alle vet, har vi et titallsystem som er oppbygd slik at når vi har telt til ti,begynner vi på en måte å telle på nytt med den forskjellen at man nå også teller tiere. Når man så har telt ut tiere (dvs. 10 10-ere), begynner vi også å telle hundre osv. Hvis vi lar tallene representere lengder (millimeter), får vi ei tallinje som er vist nedenfor.

Tall-linja har den fordelen at den raskt gir oss en oversikt over størrelseforholdet mellom to tall (lengder). Alle lengdene regnes fra null. Vi ser f.eks. at en tier er ti ganger så stor (lang) som en ener og en hundrer er ti ganger så stor (lang) som en tier. Tallinja ovenfor gir oss altså et visuelt bilde av de sanne forholdene mellom tall (lengder). Men det er klart at metoden har visse begrensninger.
Hovedbegrensningen med metoden ovenfor er at de lengdene som skal sammenliknes, må være ganske like for at metoden skal være brukbar. Man kan f.eks.ikke sammenlikne avstanden til sola og avstanden til nærmeste stjerne på ei slik tall-linje . I kosmologien overkommer man dette problemet ved å innføre ei logaritmisktall-linje. For å forstå slike tall-linjer kan man tenke seg at man velger ut alle lengder på den forige tall-linja hvor man måtte utvide med en tierpotens eller ett siffer (1,10,100osv) Man avsetter så disse som punkter langs den nye tallinje med lik avstand mellom. Se fig.
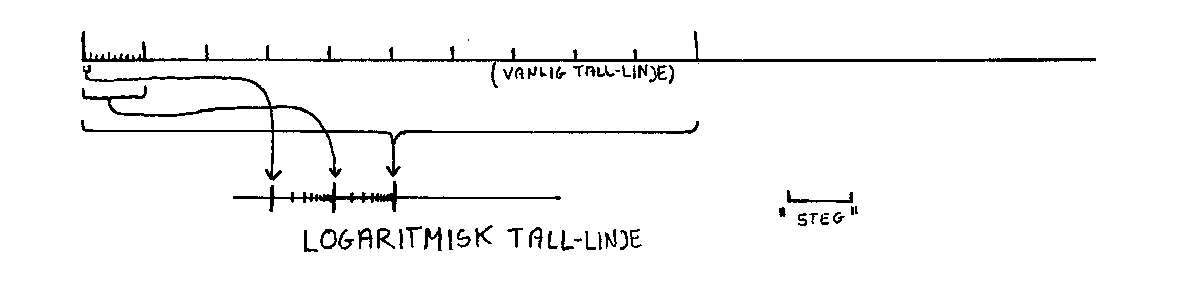
Det er nå klart at avstander langs den nye tallinja ikke blir sanne avstander . Vi kan likevel sammenlikne avstander da vi vet at hver avstand på tallinja er 10 ganger så lang som den som ligger et"steg" til venstre. En avstand blir da 100 ganger så lang som den som ligger to "steg" til venstre osv. Vi har her tenkt oss at tallinja representerer avstander, men det er ikke noe i vegen for å tenke seg at tallinja representerer tidsrom. Det krever nok litt trening for å fullt ut kunne nyttiggjøre seg slike logaritmiske tallinjer . Vi vil her bruke slike tallinjer når vi skal gi en oversikt over aktuelle lengder og tidsrom. Se neste side:
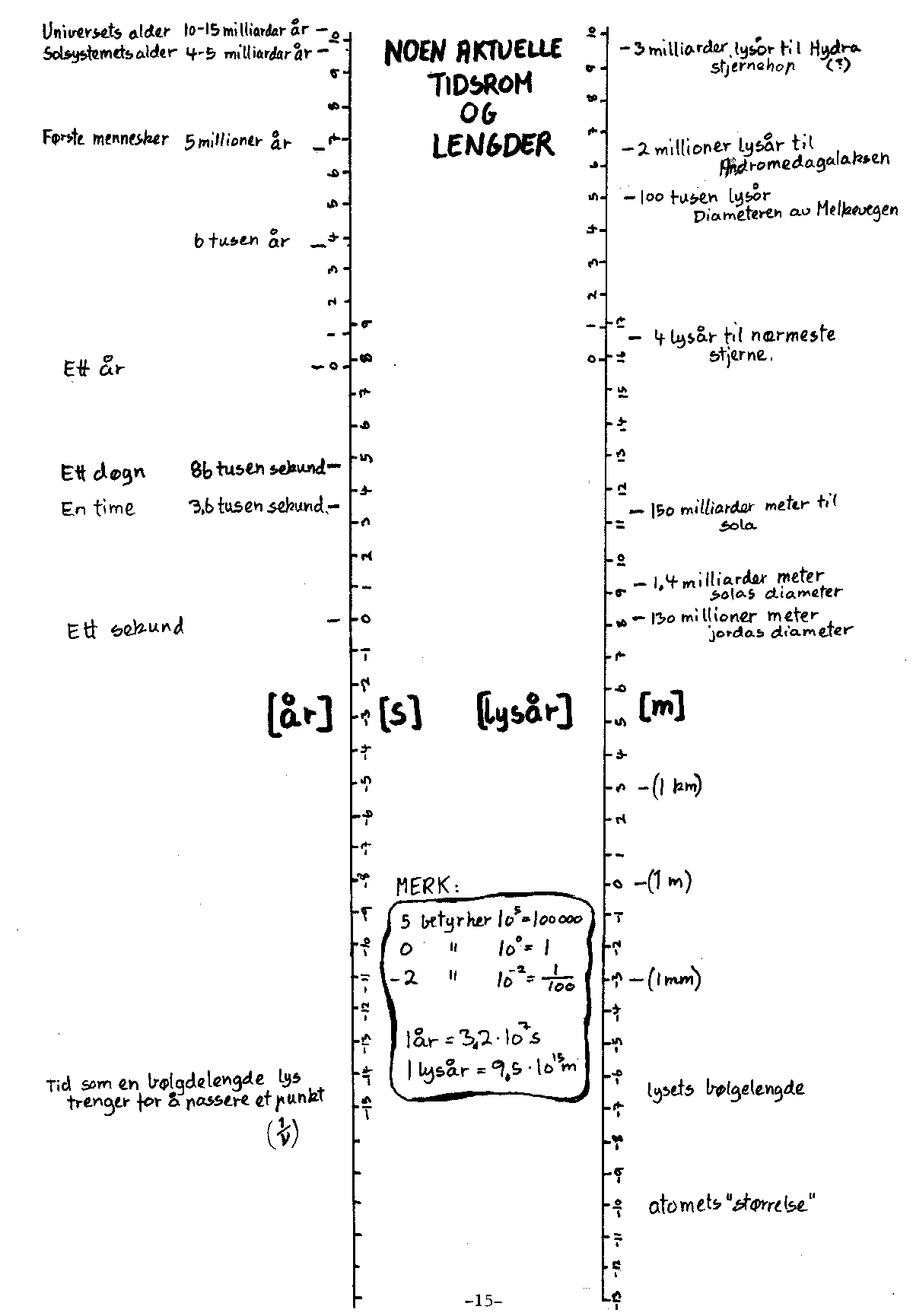
Studer talllinjene på forrige side litt. Merk spesielt hvordan de ulike lengder og tidsrom er plassert på tallinja når de ligger mellom to tierpotenser. Dette systemet innebærer at man kan gå et"steg" til venstre eller høyre uansett hvor man befinner seg på linja, og hver gang vil dette tilsvare å dividere eller multiplisere med 10. Går man et halvt "steg" til høyre betyr det at man multiplisere med ca.3. For de som synes at dette er litt vanskelig, går det an å tenke at tallene langs tallinja representerer antall siffer etter det første. Et eksempel: Solas diameter er oppgitt til å være 1.4 milliarder meter. Denne er på tallinja plassert i"9-området". Det betyr at 1-tallet har ni siffer etter seg (nuller og andre tall).
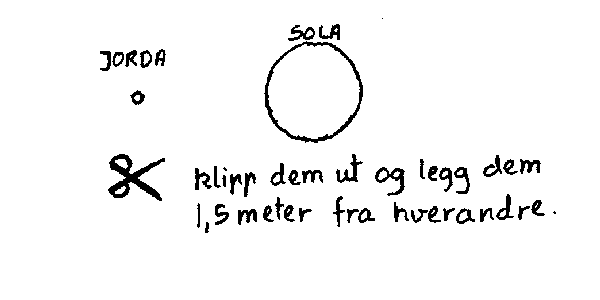
Hvordan kan man så bruke den logaritmiske tallinja foran til å danne seg et rett bilde av forholdet mellom ulike størrelser? Vi skal her vise en måte å tenk på . La oss f.eks. prøve å danne oss et bilde av størrelse forholdene mellom jorda, sola og avstanden mellom dem. Vi tenker oss gå at en millimeter på vårt papir tilsvarer 10 meter. Det betyr at jorda kan tegnes som en sirkel med diameter 1.3 mm. Solas diameter blir da 1.4 cm fordi vi må over i neste område (10-området). Avstand en mellom dem blir videre 1.5 meter. Man kan så f.eks. klippe ut sola og jorda og legge dem med 1.5 meters mellomrom på gulvet. Nå er det ganske enkelt å forestille seg disse forholdene når det er snakk om størrelser mellom en millimeter og la oss si 100 meter. Vi vil derfor også seinere bruke denne metoden for å danne oss et bilde av universet.
A6: Oppgaver
Tenk deg at det virkelig finnes endimensjonale og todimensjonale vesener i tillegg til oss som jo er tredimensjonale. Prøv å bestem hvor mange dimensjoner som kreves for å gjennomføre de nedenfornevnte aktivitetene.
a) Klappe i hendene
b) Sykle
c) Håndhilse
d) Kaste ball
e) Klippe papir med saks
f) Hvor mange"vegger"må de ulike vesenene ha i pengeskapene sine for at ingen fra samme dimensjon skal kunne stjele fra dem?


2Krummingen til ei flate er definert som 1/rR hvor r og R er henholdsvis
den minste og den største radien i de sirklene som tangerer flata, og som
samtidig står normalt på flata i det punktet vi måler krumminga. Figuren
nedenfor viser den største og minste sirkelen som tangerer overflata
til ei skje. Hvis alle tangentsirklene er på samme sida av flata sier
vi at krumminga er positiv. Hvis flata får tangentsirkler på begge sidene
sier vi at krumminga er negativ. Hvis ei av tangeringslinjene til flata er rett
(tilsvarer at radien er uendelig) har flata null krumming.
Bruk definisjonen ovenfor til å avgjøre om krumminga er positiv,
null eller negativ der pilene peker.
Hva blir verdien av krumminga i følgende tilfeller:
i) En ball med radius 0.2 meter?
j) Et rett rør med radius 1.5 meter?
k) Ytterkanten av et bøyd tør med radius 0.1 meter og bøyningsradius 10 meter?
1) Innerkanten av det samme røret?
3Tenk deg en nærsynt maur som driver løpetrening på et strikk. Den måler
hastigheten ved å avsette merker på strikket med en fast avstand ax mellom
hvert merke. Dessuten har den ei klokke og den tida det tar å løpe fra et merke
til neste kaller vi Δt. Hastigheten blir da Δx/Δt.
a)Hva vil mauren oppleve hvis strikket strekkes?
b)Hva vil mauren oppleve hvis den selv vokser og blir større mens strikket
forblir uforandret ?
c)Hva vil mauren oppleve hvis den vokser i takt med strikkets utvidelse?
d)Hva vil mauren oppleve hvis klokka begynner å gå seinere?
Merk at mauren ikke har noen muligheter for å kontrollere om lengdene og
tidsrommene den bruker forandres. Den vil derfor sannsynligvis anta at
disse ikke forandres og at de ulike hastighetene derfor skyldes dagsformen.
Mauren regner med andre ord med at lengda mellom to merker på strikket
og den tida som klokka viser er absolutte størrelser.
e) Vi som studerer det hele utenfra vil kunne si at strikket strekkes fordi vi ser det i forhold til andre lengder i vår verden.
Men er det egentlig mulig helt sikkert å si at de lengdene vi opplever rundt oss til daglig er absolutte? Hvem avgjør hva som er absolutt? Hva slags krav må vi stille til det som vi bruker for å måle lengder med?
4Fordi det meste på jorda utvider seg når temperaturen øker finnes der ikke noen metermål som alltid viser rett lengde. Hvis man imidlertid vet hvor mye en meterstav av for eksempel jern utvider seg, kan man alltid bruke den for å finne absolutte lengder hvis vi kjenner temperaturen på stedet. Lengdeutvidlesekoeffesienten for jern er ca. 0.000012 og denne forteller hvor mye en lengde på en meter vil utvide seg pr grad. Tenk deg at du har en meterstav av jern som viser nøyaktig en meter ved 20 grader Celsius. Hvor lang vil den være ved 40 grader Celsius? Hvor langt på denne meterstaven vil en virkelig meter nå ved 40 grader Celsius?
5 Tegn et rom-tid diagram. Tenk deg at vi mottar et radiosignal fra et planetsystem som ligger 4 lysår borte. Vi sender umiddelbart et radiosignal tilbake. Tegn verdenslinja for disse radiosignalene. Merk av hvor det andre planetsystemet er i rom tid diagrammet da vi mottak signalet.
6 Melkevegen og Adromedagalaksen er to omtremt like store galakser. Lag en figur som viser forholdet mellom størrelsen til disse og avstanden mellom dem (Avstandene er oppgitt i tillegg)